- 610.00 KB
- 2021-04-12 发布
包头一中2017--2018学年第一学期期中考试试题
高二理科数学
一、 选择题(每题只有一个正确选项,每题5分,共60分)
1、命题“ ” 的否定是( )
A. B.
C. D.
2、 已知双曲线的左右焦点分别为,若双曲线左支上有一点到右焦点距离为18,为中点,为坐标原点,则等于( )
A. B.8 C.2 D.4
3、设,若( )
A. B. C. D.ln 2
4、 “”是“方程表示椭圆”的( )
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
5、与双曲线有共同的渐近线,且经过点的双曲线的方程为( )A. B. C. D.
6、如果命题“”是真命题,则( )
A.命题p、q均为假命题 B.命题p、q中至少有一个是真命题
C.命题p、q均为真命题 D.命题p、q中至多有一个是真命题
7、若中心在原点,对称轴为坐标轴的双曲线的渐近线方程式为
,则该双曲线的离心率为( )A.或 B.或3 C. D.
8、已知椭圆的离心率为,四个顶点构成的四边形的面积为4,过原点的直线 (斜率不为零)与椭圆交于两点,为椭圆的左、右焦点,则四边形的周长为( )A.4 B. C.8 D.
9、函数 满足( )
A. - 2 B、 2 C 、 0 D 、 1
10、、已知抛物线的焦点为F,直线与C交于A,B(A在x轴上方)两点.若,则的值为( )A. B. C.2 D.3
11、已知双曲线的离心率为2.若抛物线的焦点到双曲线的渐近线的距离为2,则抛物线的方程为( )
(A) (B) (C) (D)
12、在椭圆上有一点,是椭圆的左、右焦点,为直角三角形,则这样的点有( )A.3个 B.4个 C.6个 D.8个
二、填空题(每小题5分,共20分)
13、以双曲线-=1的焦点为顶点,顶点为焦点的椭圆方程为________.
14、已知函数,则____________。
15、右图是抛物线形拱桥,当水面在时,拱顶离水面2米,水面宽4米,水位下降2米后(水足够深),水面宽 米。
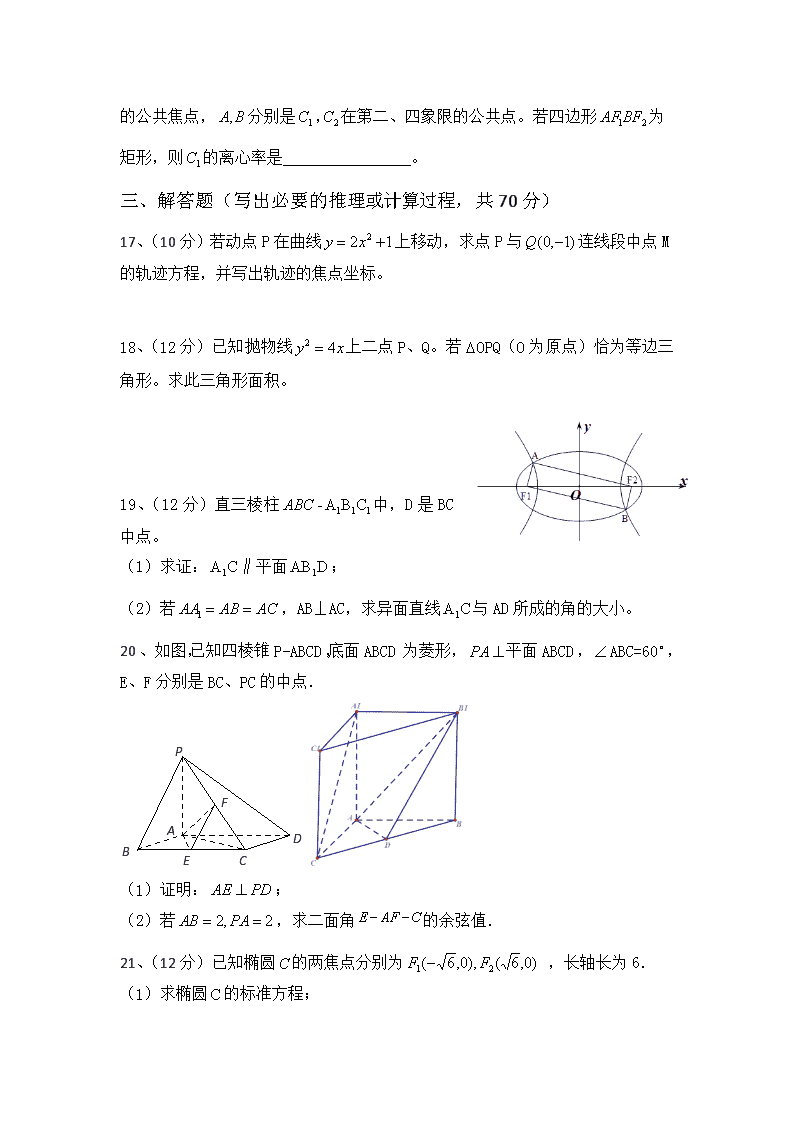
16.如图,是椭圆与双曲线:
的公共焦点,分别是,在第二、四象限的公共点。若四边形为矩形,则的离心率是________________。
三、 解答题(写出必要的推理或计算过程,共70分)
17、(10分)若动点P在曲线上移动,求点P与连线段中点M的轨迹方程,并写出轨迹的焦点坐标。
18、(12分)已知抛物线上二点P、Q。若OPQ(O为原点)恰为等边三角形。求此三角形面积。
19、(12分)直三棱柱中,D是BC中点。
(1) 求证:∥平面;
(2) 若,AB⊥AC,求异面直线与AD所成的角的大小。
20、如图,已知四棱锥P-ABCD,底面ABCD为菱形,平面ABCD,ABC=60,E、F分别是BC、PC的中点.
P
B
E
C
D
F
A
(1)证明:;
(2)若,求二面角的余弦值.
21、(12分)已知椭圆的两焦点分别为 ,长轴长为6.
(1)求椭圆的标准方程;
(2)已知过点且斜率为1的直线交椭圆与两点,求的面积.
22、已知动点M(x,y)到直线:x = 4的距离是它到点N(1,0)的距离的2倍.
(1) 求动点M的轨迹C的方程;
(2) 是否存在过点N的直线m与轨迹C交于A, B两点. 使得以AB为直径的圆恰过原点。如果存在,求出直线m的方程;如果不存在,说明理由。
包头一中2017--2018学年第一学期期中考试试题
高二理科数学 答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
C
D
B
B
C
D
A
C
C
D
D
C
13、 14、 15、 16、
17、 设,
所以,得,焦点坐标()
18、
19、 (1)连结,可证平行于OD,
可证∥平面;
(2) ,则为所求,异面直线角的大小为
(向量法相应给分)
20、(1)证明:由四边形为菱形,,可得
为正三角形.
因为为的中点,所以.又,因此.
因为平面,平面,所以.
而平面,平面且,
所以平面.又平面,所以.
(2)解法一:因为平面,平面,所以平面平面.
过作于,则平面,过作于,连接,
则为二面角的平面角,
在中,,,
又是的中点,在中,,
又, 在中,,
即所求二面角的余弦值为.
解法二:由(1)知两两垂直,以为坐标原点,建立如图所示的空间直角坐标系,又分别为的中点,所以
P
B
E
C
D
F
A
y
z
x
,
,所以.设平面的一法向量为,
则因此
取,则,因为,,,
所以平面,故为平面的一法向量.又,
所以.
因为二面角为锐角,所以所求二面角的余弦值为.
21、(1);
(2)的方程为②把②带入①得化简并整理得
,
22、(1)设,由,得
(2)显然若存在这样的直线,其斜率不为0.
假设存在这样的直线,设其方程为
得。
若AB为直径的圆过O,则
,无实数解。所以不存在。