【推荐】专题05 小题易丢分-2017届高三上学期期末考试数学（理）备考黄金30题 16页

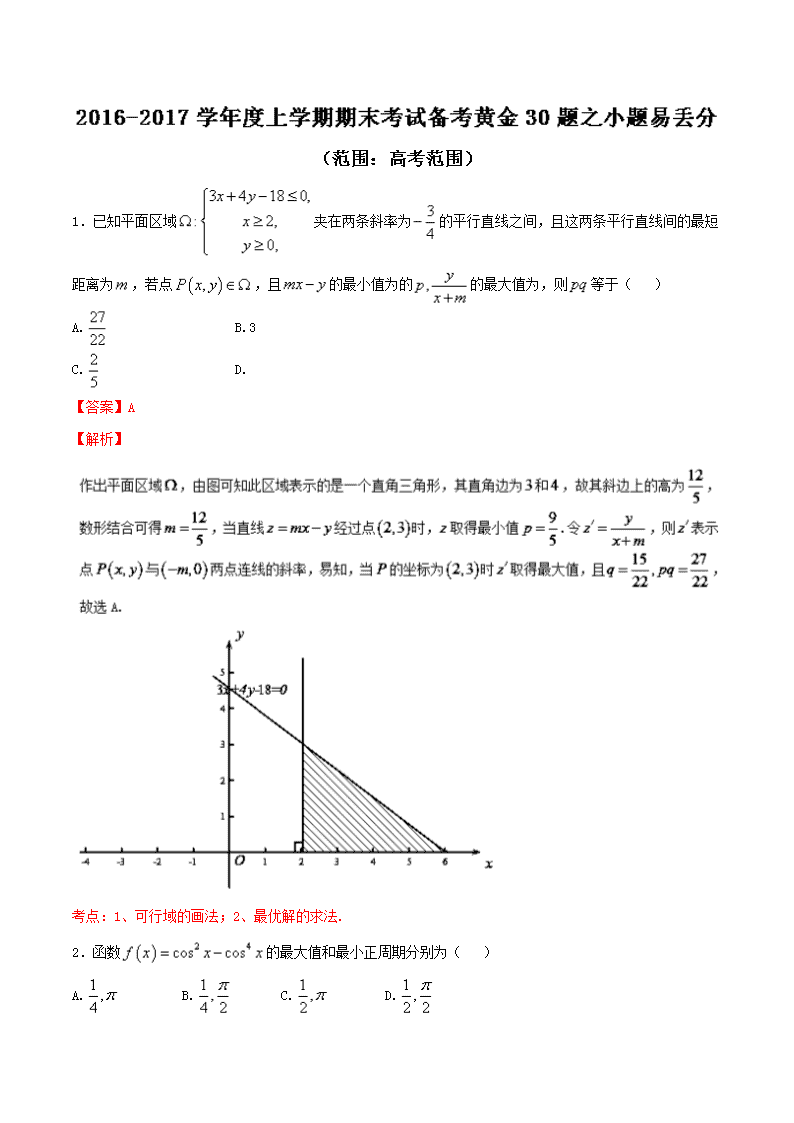
（范围：高考范围） 1．已知平面区域 3 4 18 0, : 2, 0, x y x y        夹在两条斜率为 3 4  的平行直线之间，且这两条平行直线间的最短 距离为 m ，若点  ,P x y  ，且 mx y 的最小值为的 , yp x m 的最大值为，则 pq 等于（ ） A. 27 22 B.3 C. 2 5 D. 【答案】A 【解析】 考点：1、可行域的画法；2、最优解的求法. 2．函数   2 4cos cosf x x x  的最大值和最小正周期分别为（ ） A. 1 ,4  B. 1 ,4 2  C. 1 ,2  D. 1 ,2 2  【答案】B 【解析】    2 2 1 1 cos4 1 1cos 1 cos cos44 2 8 8 xf x x x x      ，最大值为 1 4 ，最小正周期为 2  . 考点：三角恒等变换. 3．若函数   3 2 6f x x ax x    在 0 1， 内单调递减，则实数的取值范围是（ ） A. 1a  B. 1a  C. 1a  D. 0 1a  【答案】B 【解析】 考点：导数与函数单调性的关系. 4．现定义 cos sinie i    ，其中为虚数单位，为自然对数的底数， R  ，且实数指数幂的运算性质 对 ie  都适用，若 0 5 2 3 2 4 4 5 5 5cos cos sin cos sina C C C       ， 1 4 3 2 3 5 5 5 5 5cos sin cos sin sinb C C C       ，那么复数 a bi 等于（ ） A． cos5 sin5i  B． cos5 sin5i  C．sin5 cos5i  D．sin5 cos5i  【答案】A 【解析】 0 5 2 3 2 4 4 1 4 3 2 3 5 5 5 5 5 5 5 5cos cos sin cos sin ( cos sin cos sin sin )a bi C θ C θ θ C θ C θ θ C θ θ C θ i       0 5 1 4 2 3 2 2 3 2 3 3 4 4 4 5 5 5 5 5 5 5 5 5cos cos sin cos sin cos sin cos sin sinC θ C θ i θ C θ i θ C θ i θ C θ i C i θ          5(cos sin ) cos5 sin5θ i θ θ i θ    ．故选 A． 考点：复数的运算，二项式定理． 5．已知体积为 4 6 的长方体的八个顶点都在球 O 的球面上，在这个长方体经过同一个顶点的三个面中， 如果有两个面的面积分别为 2 3 、 4 3 ,那么球O 的体积等于（ ） A． 32 3  B．16 7 3  C． 33 2  D．11 7 2  【答案】A 【解析】 考点：球与几何体的外接和体积的计算. 6．设等比数列{an}的前 n 项和为 Sn．若 S2=3，S4=15，则 S6=（ ） A．31 B．32 C．63 D．64 【答案】C 【解析】 由等比数列的性质可得 S2，S4﹣S2，S6﹣S4 成等比数列，代入数据计算可得． 解：S2=a1+a2，S4﹣S2=a3+a4=（a1+a2）q2，S6﹣S4=a5+a6=（a1+a2）q4， 所以 S2，S4﹣S2，S6﹣S4 成等比数列， 即 3，12，S6﹣15 成等比数列， 可得 122=3（S6﹣15）， 解得 S6=63 故选：C 考点：等比数列的前 n 项和． 7．下列四个函数中，在 0x  处取得极值的函数是（ ） ① 3y x ；② 2 1y x  ；③ y x ；④ 2xy  A．①② B．①③ C．③④ D．②③ 【答案】D 【解析】 ①中， 23 0y x   恒成立，所以函数在 R 上递增，无极值点；②中 2y x  ，当 0x  时函数单调递增， 当 0x  时函数单调递减，且 0| 0xy   ，符合题意；③中结合该函数图象可知当 0x  时函数单调递增，当 0x  时函数单调递减，且 0| 0xy   ，符合题意；④中，由函数的图象知其在 R 上递增，无极值点，故选 D． 考点：函数的极值． 8．已知定义在 R 上的可导函数 ( )f x 的导函数为 ' ( )f x ，满足 ' ( ) ( )f x f x ，且 ( 2)f x  为偶函数， (4) 1f  ，则不等式 ( ) xf x e 的解集为（ ） A． ( 2, )  B． (0, ) C． (1, ) D． (4, ) 【答案】B 【解析】 考点：函数的奇偶性，单调性． 9．给出如下四个命题： ①若“p 且 q”为假命题，则 p、q 均为假命题； ②命题“若 a＞b，则 2a＞2b﹣1”的否命题为“若 a≤b，则 2a≤2b﹣1”； ③“ ∀ x∈R，x2+1≥1”的否定是“ ∃ x∈R，x2+1≤1； ④在△ABC 中，“A＞B”是“sinA＞sinB”的充要条件． 其中不正确的命题的个数是（ ） A．4 B．3 C．2 D．1 【答案】C 【解析】 ①若“p 且 q”为假命题，则 p、q 中有一个为假命题，不一定 p、q 均为假命题；②根据命题写出其否命题 时，只须对条件与结论都要否定即得；③根据由一个命题的否定的定义可知：改变相应的量词，然后否定 结论即可；④在△ABC 中，根据大边对大角及正弦定理即可进行判断． 解：①若“p 且 q”为假命题，则 p、q 中有一个为假命题，不一定 p、q 均为假命题；故错； ②根据命题写出其否命题时，只须对条件与结论都要否定即得，故命题“若 a＞b，则 2a＞2b﹣1”的否命题 为“若 a≤b，则 2a≤2b﹣1”；正确； ③根据由一个命题的否定的定义可知：改变相应的量词，然后否定结论：“ ∀ x∈R，x2+1≥1”的否定是 “ ∃ x∈R，x2+1＜1；故错； ④在△ABC 中，根据大边对大角及正弦定理即可得：“A＞B”是“sinA＞sinB”的充要条件．故正确． 其中不正确 的命题的个数是：2． 故选 C． 考点：命题的否定；正弦函数的单调性． 10．如图所示，在两个圆盘中，指针在本圆盘没个数所在区域的机会均等，那么两个指针同时落在奇数所 在区域的概率是（ ） A． 4 9 B． 2 9 C． 2 3 D． 1 3 【答案】A 【解析】 考点：对立事件、互斥事件. 11．设 nS 为等差数列{ }na n的前 项和，若 3 9 63, 27a S S   ，则该数列的首项 1a 等于（ ） A． 6 5  B． 3 5  C． 6 5 D． 3 5 【答案】D 【解析】 设等差数列 na 的公差为 d ，由 3 9 63, 27a S S   ，可得   1 6 1 2 3 5 27 a d a a d        ，解得 1 23a  ．故选 A． 考点：等差数列的通项公式及其前项和公式 12．为了从甲乙两人中选一人参加数学竞赛，老师将二人最近 6 次数学测试的分数进行统计，甲乙两人的 平均成绩分别是 x甲 、 x乙 ，则下列说法正确的是（ ） A． x x 乙甲 ，乙比甲成绩稳定，应选乙参加比赛 B． x x 乙甲 ，甲比乙成绩稳定，应选甲参加比赛 C． x x 乙甲 ，甲比乙成绩稳定，应选甲参加比赛 D． x x 乙甲 ，乙比甲成绩稳定，应选乙参加比赛 【答案】D 【解析】 考点：1、平均值的算法；2、茎叶图的应用. 13．不等式组 1, 2 4 x y x y      的解集为 D，下列命题中正确的是（ ） （A）  , , 2 1x y D x y     （B）  , , 2 2x y D x y     （C）  , , 2 3x y D x y    （D）  , , 2 2x y D x y    【答案】B. 【解析】 如下图所示，画出不等式组所表示的区域，作直线： 2 0x y  ，平移， 从而可知当 2x  ， 1y   时， min( 2 ) 0x y  ，即 2 0x y  ，故只有 B 成立，故选 B． 考点：线性规划． 14．设抛物线 y2=8x 的焦点为 F，准线为 l，P 为抛物线上一点，PA⊥l，A 为垂足．如果直线 AF 的斜率为 ， 那么|PF|=（ ） A． B．8 C． D．16 【答案】B 考点：抛物线的简单性质；抛物线的定义． 15．下列命题正确的是（ ） A．若两条直线和同一个平面所成的角相等，则这两条直线平行 B．若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行 C．若一条直线平行于两个相交平面，则这条直线与这两个平面的交线平行 D．若两个平面都垂直于第三个平面，则这两个平面平行 【答案】C 【解析】 A、若两条直线和同一个平面所成的角相等，则这两条直线平行、相交或异面，故 A 错误； B、若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行或相交，故 B 错误； C、设平面α∩β=a，l∥α，l∥β，由线面平行的性质定理，在平面α内存在直线 b∥l，在平面β内存在 直线 c∥l，所以由平行公理知 b∥c，从而由线面平行的判定定理可证明 b∥β，进而由线面平行的性质定 理证明得 b∥a，从而 l∥a，故 C 正确； D，若两个平面都垂直于第三个平面，则这两个平面平行或相交，排除 D． 故选 C． 考点：空间中直线与平面之间的位置关系；命题的真假判断与应用． 16．若 的最小正周期为 ， ，则（ ） A. 在 单调递增 B. 在 单调递减 C. 在 单调递增 D. 在 单调递减 【答案】D 【解析】 考点：三角函数的图象与性质. 17．如图 1，已知正方体 1 1 1 1ABCD A B C D 的棱长为， , ,M N Q 分别是线段 1 1 1 1, ,AD B C C D 上的动点，当 三棱锥Q BMN 的俯视图如图 2 所示时，三棱锥Q BMN 的体积为（ ） A． 31 2 a B． 31 4 a C． 32 4 a D． 31 12 a 【答案】D 【解析】 由三视图知,Q 与 1D 重合, N 与G 重合, M 在 1AD 中点处，所以可得， Q BMN N BMQV V  2 3 1 1 2 2 1 3 3 4 2 2O BMQ BMQV S DM a a a         ,故选 D. 考点：1、几何体的三视图；2、几何体的表面积. 18．已知集合 { | 2 0}A x x   ， 2{ | 0 log 2}B x x   ，则 ( )RC A B 是（ ） A．{ | 2 4}x x  B．{ | 2}x x  C．{ | 2 4}x x x 或 D．{ | 2 4}x x x 或 【答案】D 【解析】 考点：1、集合的交集运算；2、集合的补集运算． 19．某几何体的主视图和左视图如图（1），它的俯视图的直观图是矩形 1 1 1 1O A B C 如图（2），其中 1 1 6O A  ， 1 1 2O C  ，则该几何体的侧面积为（ ） A． 48 B． 64 C．96 D．128 【答案】C 【解析】 由已知中的三视图可得该几何体是一个四棱柱， ∵它的俯视图的直观图是矩形 1 1 1 1O A B C ， 1 1 1 16, 2O A O C  ， ∴它的俯视图的直观图面积为 12， ∴它的俯视图的面积为： 24 2 ， ∴它的俯视图 的俯视图是边长为：6 的菱形， 棱柱的高为 4 故该几何体的侧面积为：4×6×4=96 考点：由三视图求面积、体积 20．已知双曲线   2 2 2 2: 1 0, 0x yE a ba b     的左焦点为  2,0F  ，过点 F 的直线交双曲线于 ,A B 两点， 若 AB 的中点坐标为 3, 1  ，则 E 的方程为（ ） A． 2 2 136 4 x y  B． 2 2 13 yx   C． 2 2 13 x y  D． 2 2 14 36 x y  【答案】C 【解析】 考点：直线与圆锥曲线位置关系． 21．如图，在圆 2 2 4x y  上任取一点 P ，过点 P 作轴的垂线段 PD ， D 为垂足．当点 P 在圆上运动时， 线段 PD 的中点 M 的轨迹是椭圆，那么这个椭圆的离心率是（ ） A． 1 2 B． 1 4 C． 2 2 D． 3 2 【答案】D． 考点：椭圆的标准方程及其性质． 22．设 na 是等比数列，公比 2q ， nS 为 na 的前项和，记 )(,17 1 2    Nna SST n nn n ，设 0nT 为数列 nT 的最大项，则 0n （ ） A.2 B.3 C.4 D.5 【答案】A 【解析】    1212 12 1 1   n n n aaS ，    1212 12 2 1 2 1 2   n n n aaS ， n n aa 211  ，∴     98172 162172 12121717 1 2 11 1 2         n n n nn n nn n a aa a SST ，当且仅当 2n 时取等号，∴数 列 nT 最大项为 2T ，则 2n .故选：A. 考点：数列的求和. 23.一个几何体的三视图如图所示（单位 cm ），则该几何体的体积为______ 3cm ． 【答案】16 【解析】 考点：三视图、棱锥的体积. 24．已知 ABC 的三个内角 A B C， ， 的对边依次为 a b c， ， ，外接圆半径为 1，且满足 tan 2 tan A c b B b  ， 则 ABC 面积的最大值为___________. 【答案】 3 3 4 【解析】 试题分析:由 tan 2 tan A c b B b  可得 B BC AB BA sin sinsin2 cossin cossin  ,即 1 sinsin2 cos cossin BC A BA  ,也即 ABACBA cossincossin2cossin  ,故 ACBA cossin2)sin(  ,也即 1cos2 A ,则 060A ,由 正弦定理可得 3sin2  Aa ,再由余弦定理可得 cbbc 3)(3 2  ,即 cbbccb 4)(33 2  ,所以 3cb ,故 4 33 4 3sin2 1  bcAbcS ABC ,应填 3 3 4 . 考点：三角变换基本不等式正弦定理余弦定理等有关知识的综合运用． 25．一个社会调查机构就某地居民的月收入调查了10000人，并根据所得数据画了样本的频率分布直方图 （如下图）．为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10000人中再用分层抽样方法 抽出100人作进一步调查，则在 2500,3500 （元）月收入段应抽出人． 【答案】40 【解析】 由图（2500，3500 元/月）收入段的频率是 0.0005×500+0.0003×500=0.4 故用分层抽样方法抽出 100 人作进一步调查，则在（2500，3500 元/月）收入段应抽出人数为 0.4×100=40 考点：频率分布直方图；分层抽样方法 26．已知 P（x，y）是双曲线 =1 上任意一点，F1 是双曲线的左焦点，O 是坐标原点，则 的 最小值是． 【答案】4﹣2 【解析】 考点：双曲线的简单性质． 27．函数   21ln 52f x x x x    的单调递增区间为__________. 【答案】 1 50, 2       【解析】 试题分析:因 11)(/  xxxf ，注意到 0x ，故解 011  xx 可得 2 150  x .故应填答案 1 50, 2       . 考点：导数与函数单调性的关系及综合运用. 28．三棱锥 D ABC 内接于表面积为100 的球面, DA  平面 ABC ,且 8, , 30AB AC BC BAC    , 则三棱锥 D ABC 的体积为. 【答案】16 3 【解析】 考点：球的表面积和体积. 29．已知实数 x、y 满足 2 2 0 3 x y x y y         ，则 2Z x y  的取值范围是. 【答案】[ 5,7] 【解析】 画出可行域如图 由 2z x y  可变形得 2y x z  ，当直线经过点 B 时取得最小值，直线经过点 C 时取得最大值，所以取得 最小值是 2 ( 1) 3 5     ，取得最大值是 2 5 3 7   ，可得的取值范围是[ 5,7] . 考点：利用线性规划求最值. 30．下列结论正确的是 ①在某项测量中，测量结果服从正态分布 2(1, )( 0)N    .若在 (0,1) 内取值的概率为 0.35，则在 (0,2) 内 取值的概率为 0.7； ②以模型 kxy ce 去拟合一组数据时，为了求出回归方程，设 lnz y ，其变换后得到线性回归方程 0.3 4z x  ，则 4c e ； ③已知命题“若函数 ( ) xf x e mx  在 (0, ) 上是增函数，则 1m  ”的逆否命题是“若 1m  ，则函数 ( ) xf x e mx  在 (0, ) 上是减函数”是真命题； ④设常数 ,a b R ，则不等式 2 ( 1) 0ax a b x b     对 1x  恒成立的充要条件是 1a b  . 【答案】①②④ 【解析】 考点：1.正态分布；2.线性回归方程；3.四种命题；4.充分条件与必要条件.