- 789.50 KB
- 2021-04-12 发布
洛阳市2016——2017学年高中三年级第一次统一考试
数学试卷(理科)
第Ⅰ卷(选择题,共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.
1.已知为虚数单位,若实数满足,则的模为
A. 1 B. C. D. 2
2.已知集合,则
A. B. C. D.
3.已知,则且是且的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D.既不充分也不必要条件
4.一枚骰子先后抛掷两次,并记朝上的点数分别为m,n,已知m为2或4时,的概率为
A. B. C. D.
5.已知下列函数中是周期函数且最小正周期为的是
A.
B.
C.
D.
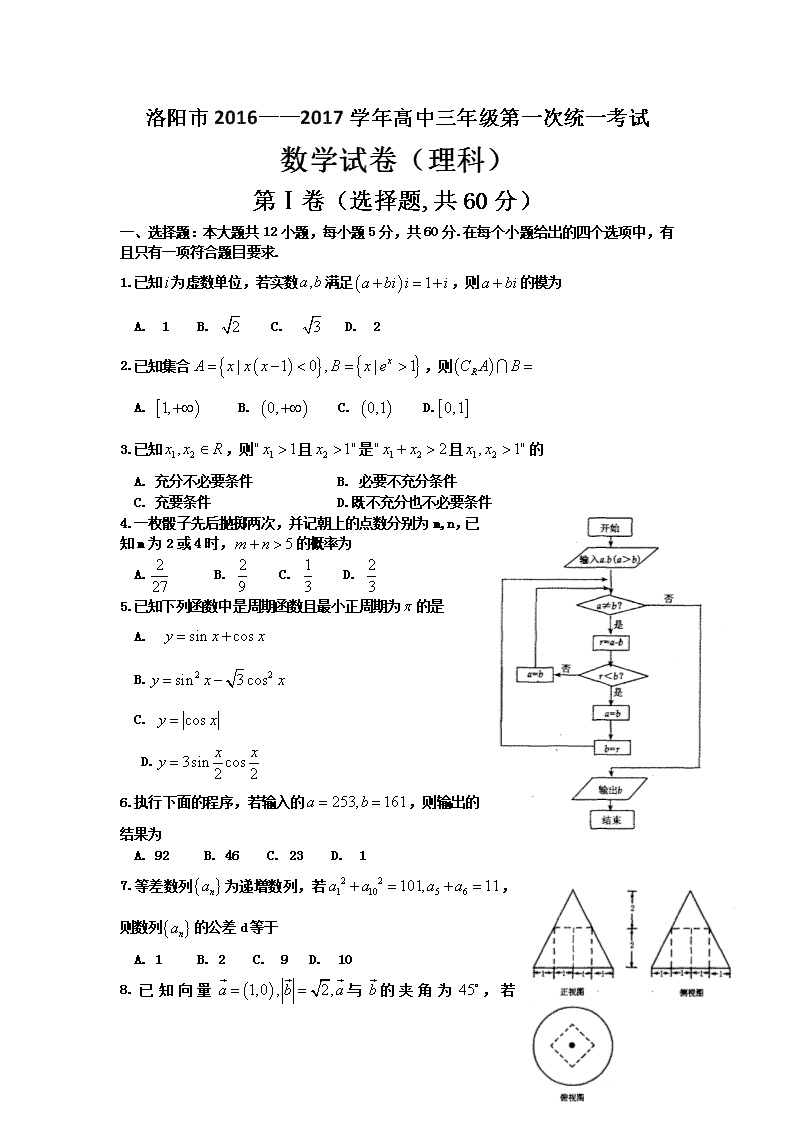
6.执行下面的程序,若输入的,则输出的结果为
A. 92 B. 46 C. 23 D. 1
7.等差数列为递增数列,若,则数列的公差d等于
A. 1 B. 2 C. 9 D. 10
8.已知向量与的夹角为,若
,则在方向的投影为
A. B. C. 1 D.
9.已知简单组合体的三视图如图所示,则此简单组合体的体积为
A. B. C. D.
10.已知实数满足条件,若取得最大值时的最优解有且只有一个,则实数的取值集合为
A. B. C. D.
11.等比数列的首项为,公比为,前项和为,则当时,的最大值和最小值之和为
A. B. C. D.
12.四面体中,,则此此四面体外接球的表面积为
A. B. C. D.
二、填空题:本大题共4小题,每小题5分,共20分.
13.已知双曲线的一条渐近线方程为,则双曲线C的离心率为 .
14.若,则的二项展开式中的系数为 .
15.已知抛物线的焦点为F,直线AB与抛物线C相交于A,B两点,若,则弦AB的中点到抛物线C的准线的距离为 .
16.已知函数(为自然对数的底数),若对任意的正数,当时,都有成立,则实数m的取值范围为 .
三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明或推理、验算过程.
17.(本题满分12分)如图,平面四边形ABCD中,
(1)若,且,求的长;
(2)若,求的取值范围.
18.(本题满分12分)如图,四边形和四边形均为直角梯形,,二面角是直二面角,
(1)证明:在平面上,一定存在过点C的直线与直线平行;
(2)求二面角二余弦值.
19.(本题满分12分)雾霾天气对人体健康有害,应对雾霾污染、改善空气质量是当前的首要任务是控制PM2.5,要从压减燃煤、严格控产、调整产业、强化管理、联防联控、依法治理等方面采取重大举措,聚焦重点领域,严格考核指标.某省环保部门为加强环境执法监管,派遣四个不同的专家组对A,B,C三个城市进行雾霾落实情况抽查.
(1)若每个专家组随机选取一个城市,四个专家组选取的城市可以相同,也可以不同,求恰有一个城市没有专家组选取的概率;
(2)每个城市都要有四个专家组分别对抽查情况进行评价,并对所选取的城市进行评价,每个专家组给检查到的成绩评价为优的概率为,若四个专家组均评价为优,则检查通过,不用复检,否则要进行复检,设需进行复检的城市个数为X,求X的分布列和期望.
20.(本题满分12分)设椭圆的右焦点为F,右顶点为A,B,C是椭圆上关于原点对称的两点(B,C均不在x轴上),线段AC的中点为D,B,F,D三点共线.
(1)求椭圆E的离心率;
(2)设,过F的直线交E于M,N两点,直线MA,NA分别与直线交于P,Q两点,证明:以PQ为直径的圆过点F.
21.(本题满分12分)设函数
(1)讨论函数的单调性;
(2)若函数有两个零点,求满足条件的最小正整数a的值;
(3)有两个不相等的实数根,求证.
请考生从第22、23两题中任选一题作答,如果多做,则按所做的第一题计分,作答时,用2B铅笔在答题卡上把所选题目对应的题号后的方框涂黑.
22.(本题满分10分)选修4-4:坐标系与参数方程
在直角坐标系中,圆的参数方程为(为参数),以O为极点,轴的非负半轴为极轴建立极坐标系.
(1)求圆C的普通方程;
(2)直线的极坐标方程是,射线与圆C的交点为,与直线的交点为,求线段的长.
23.(本题满分10分)选修4-5:不等式选讲
已知
(1)将的解析式写出分段函数的形式,并作出其图象;
(2)若,对恒成立,求的取值范围.