2020届二轮复习专题二　力与物体的运动第1课时力与直线运动课件（43张） 43页

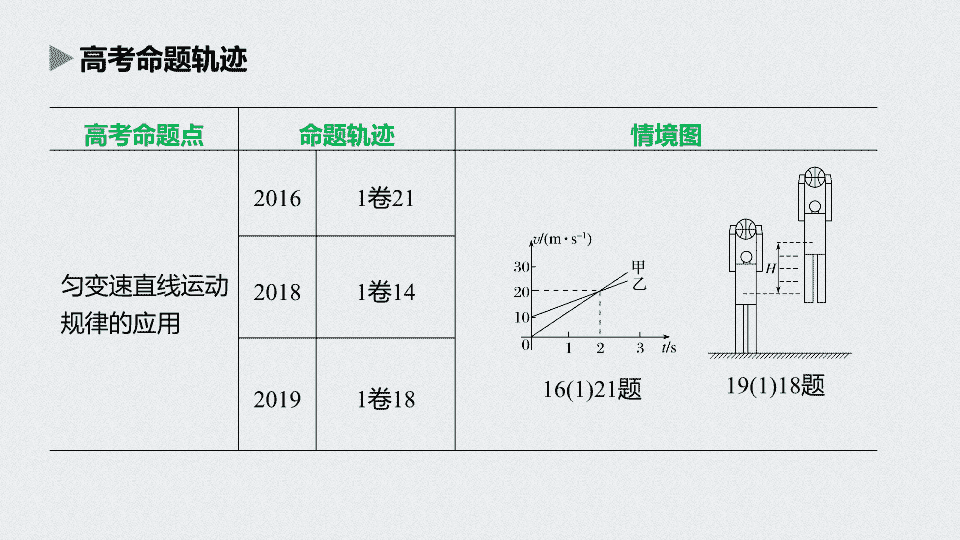
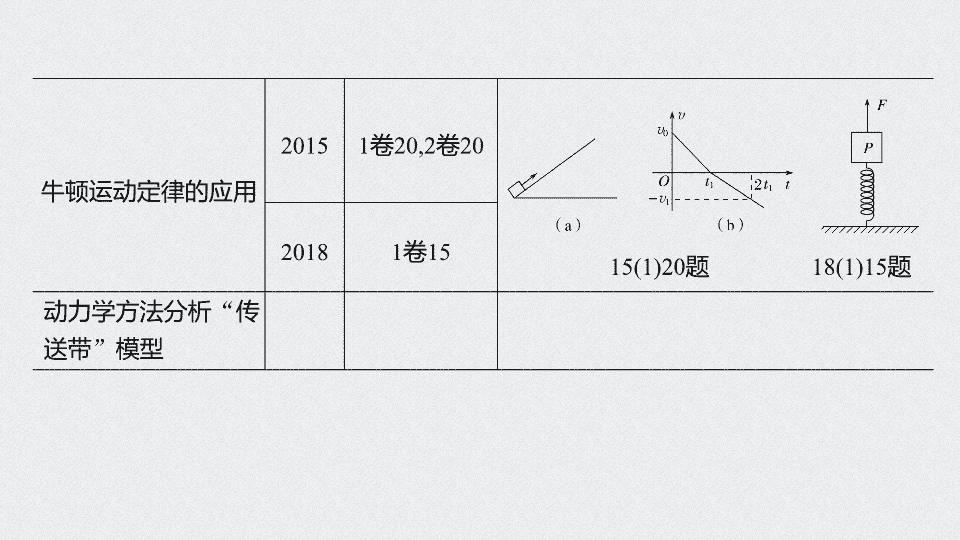
第 1 课时　力与直线运动 第一部分　专题 二　力 与物体的运动 高考命题轨迹 高考命题点 命题轨迹 情境图 匀变速直线运动规律的应用 2016 1 卷 21   2018 1 卷 14 2019 1 卷 18 16(1)21 题 19(1)18 题 牛顿运动定律的应用 2015 1 卷 20,2 卷 20   　　　 2018 1 卷 15 动力学方法分析 “ 传送带 ” 模型       15(1)20 题　　 　 18(1)15 题 动力学方法分析 “ 板 — 块 ” 模型 2015 1 卷 25 , 2 卷 25   　 　　　 2017 3 卷 25 2019 3 卷 20 15(1)25 题　　　 15(2)25 题　　 　 17(3)25 题 19(3)20 题 相关知识链接 1 . 匀变速直线运动的条件 物体所受合力 为 ， 且 与 方向 共线 . 2. 匀变速直线运动的基本规律 速度公式： v ＝ . 位移公式： x ＝ v 0 t ＋ at 2 . 速度和位移公式的推论 ： . 中间时刻的瞬时速度 ： 任意两个连续相等的时间间隔内的位移之差是一个恒量，即 Δ x ＝ x n ＋ 1 － x n ＝ a ·(Δ t ) 2 . 恒力 速度 v 0 ＋ at v 2 － v 0 2 ＝ 2 ax 3. 图象问题 (1) 速度 — 时间图线的斜率或切线斜率表示物体运动 的 ， 图线与时间轴所包围的面积表示物体运动 的 . 匀变速直线运动的 v － t 图象是一 条 直线 . (2) 位移 — 时间图线的斜率或切线斜率表示物体 的 . 4. 超重和失重 超重或失重时，物体的重力并未发生变化，只是物体对支持物 的 ( 或对悬挂物 的 ) 发生了变化 . 物体发生超重或失重现象与物体的运动 方向 ， 只取决于物体 的 方向 . 当 a 有竖直向上的分量时 ， ； 当 a 有竖直向下的分量时 ， ； 当 a ＝ g 且竖直向下时 ， . 5. 瞬时问题 应用牛顿第二定律分析瞬时问题时，应注意物体与物体间的弹力、绳的弹力和杆的弹力可以突变，而弹簧的 弹力 . 加速度 位移 倾斜 速度 压力 拉力 无关 加速度 超重 失重 完全失重 不能突变 1. 基本思路 规律方法 提炼 2. 解题关键 抓住两个分析，受力分析 和 分析 ，必要时要画运动情景示意图 . 对于多运动过程问题，还要找准转折点，特别是转折点的速度 . 3. 常用方法 (1) 整体法与隔离法：单个物体的问题通常采用隔离法分析，对于连接体问题，通常需要交替使用整体法与隔离法 . 运动情况 (2) 正交分解法：一般沿加速度方向和垂直于加速度方向进行分解，有时根据情况也可以把加速度进行正交分解 . (3) 逆向思维法：把运动过程的末状态作为初状态，反向研究问题，一般用于匀减速直线运动问题，比如刹车问题、竖直上抛运动问题 . 高考题型 1 匀变速直线运动 规律的应用 内容索引 NEIRONGSUOYIN 高考题型 2 应用 牛顿运动定律解决 “ 四类 ” 典型问题 高考题型 3 动力学 方法分析 “ 传送带 ” 模型 高考题型 4 动力学 方法分析 “ 板 — 块 ” 模型 匀变速直线运动规律的应用 题型：选择或者计算题： 5 年 3 考 高考题型 1 例 1 　 (2019· 全国卷 Ⅰ ·18) 如图 1 ，篮球架下的运动员原地垂直起跳扣篮，离地后重心上升的最大高度为 H . 上升第一 个 所 用的时间为 t 1 ，第四 个 所 用的时间为 t 2 . 不计空气阻力， 则 满足 图 1 √ 解析　 本题应用逆向思维求解，即运动员的竖直上抛运动可等同于从一定高度处开始的自由落体运动的逆运动， 拓展训练 1 　 (2019· 安徽蚌埠市第二次质检 ) 图 2 中 ae 为港珠澳大桥上四段 110 m 的等跨钢箱连续梁桥，若汽车从 a 点由静止开始做匀加速直线运动，通过 ab 段的时间为 t ，则通过 ce 段的时间为 √ 图 2 拓展训练 2 　 (2019· 广东揭阳市第二次模拟 ) 瑞士阿尔卑斯山的劳特布伦嫩跳伞区是全球最美的跳伞地之一，每年都吸引了无数跳伞爱好者汇聚此地 . 某日一跳伞爱好者 以 5 m/s 的速度竖直匀速降落，在离地面 h ＝ 10 m 时掉了一颗扣子，则跳伞爱好者比扣子晚着陆的时间为 ( 扣子受到的空气阻力可忽略 ， g 取 10 m/s 2 ) √ 解析　 由题意知，扣子做初速度为 5 m/s 、加速度为重力加速度的匀加速直线运动 ， 所以跳伞爱好者比扣子晚着陆的时间为 Δ t ＝ t 2 － t 1 ＝ 1 s ，故选 C. 应用牛顿运动定律解决 “ 四类 ” 典型问题 题型：选择题： 5 年 2 考 高考题型 2 1. 主要题型 应用牛顿运动定律解决的主要问题有：瞬时问题、连接体问题、超重和失重问题以及图象问题 . 2 . 技巧方法 (1) 解瞬时问题要注意绳、杆弹力和弹簧弹力的区别，绳和轻杆的弹力可以突变，而弹簧的弹力不能突变 . (2) 解连接体问题要充分利用 “ 加速度相同 ” 这一条件或题中特定条件，交替运用整体法与隔离法 . (3) 图象问题解题关键是：明确图象斜率、截距和面积的物理意义，应用物理公式找到两个变量间的函数关系，并注意从图象中提取有用信息或隐含条件 . 例 2 　 (2019· 福建龙岩市期末质量检查 ) 如图 3 所示，在倾角为 θ ＝ 30° 的光滑固定斜面上，物块 A 、 B 质量均为 m . 物块 A 静止在轻弹簧上端，物块 B 用细线与斜面顶端相连， A 、 B 靠在一起，但 A 、 B 之间无弹力 . 已知重力加速度为 g ，某时刻将细线剪断，下列说法正确的是 A. 细线剪断前，弹簧的弹力为 mg B. 细线剪断前，细线的拉力为 mg C. 细线剪断瞬间，弹簧的弹力发生变化 D. 细线剪断瞬间，物块 B 的加速度大小 为 √ 图 3 细线剪断瞬间，弹簧的弹力不变，故 C 错误； 例 3 　 如图 4 ，质量为 M 的缆车车厢通过悬臂固定悬挂在缆绳上，车厢水平底板上放置一质量为 m 的货物，在缆绳牵引下货物随车厢一起斜向上加速运动 . 若运动过程中悬臂和车厢始终处于竖直方向，重力加速度大小为 g ，则 A. 车厢对货物的作用力大小等于 mg B. 车厢对货物的作用力方向平行于缆绳向上 C. 悬臂对车厢的作用力大于 ( M ＋ m ) g D. 悬臂对车厢的作用力方向沿悬臂竖直向上 √ 图 4 解析　 货物随车厢一起斜向上加速运动，由牛顿第二定律可知车厢与货物的重力和悬臂对车厢作用力的合力方向应与加速度方向一致，故悬臂对车厢的作用力方向是斜向上的，选项 D 错误 ； 由于 车厢和货物在竖直方向有向上的分加速度，处于超重状态，故悬臂对车厢的作用力大于 ( M ＋ m ) g ，选项 C 正确 ； 同理 ，对车厢中货物用隔离法分析可知，车厢对货物的作用力大小大于 mg ，方向是斜向上的，但不平行于缆绳，选项 A 、 B 错误 . 例 4 　 ( 多选 )(2019· 广东深圳市第一次调研 ) 高铁已成为重要的 “ 中国名片 ” ，领跑世界 . 一辆由 8 节车厢编组的列车，从车头开始的第 2 、 3 、 6 和 7 共四节为动力车厢，其余为非动力车厢 . 列车在平直轨道上匀加速启动时，若每节动力车厢牵引力大小均为 F ，每节车厢质量都为 m ，每节车厢所受阻力均为车厢重力的 k 倍，重力加速度为 g . 则 A. 启动时车厢对乘客作用力的方向竖直向上 B. 整个列车的加速度大小为 C. 第 2 节车厢对第 1 节车厢的作用力大小为 D. 第 2 节车厢对第 3 节车厢的作用力大小为 √ √ 解析　 启动时车厢对乘客竖直方向有竖直向上的支持力，水平方向有沿列车运动方向的力，两个力的合力方向斜向上方，选项 A 错误； 对第 1 、 2 节车厢的整体，根据牛顿第二定律： F 32 ＋ F － 2 kmg ＝ 2 ma ，解得 F 32 ＝ 0 ，选项 D 错误 . 拓展训练 3 　 ( 多选 )(2019· 广东湛江市下学期第二次模拟 ) 如图 5 甲所示，在光滑水平面上，静止一质量为 M 的足够长的长木板，质量为 m 的小滑块 ( 可视为质点 ) 静止放在长木板上 . 从 t ＝ 0 时刻开始，长木板受到的水平拉力 F 与加速度 a 的关系如图乙所示，重力加速度大小 g 取 10 m/s 2 ，下列说法正确的是 图 5 A. 长木板的质量 M ＝ 1 kg B. 小滑块与长木板之间的动摩擦因数为 0.5 C. 当 F ＝ 6.5 N 时，长木板的加速度大小为 2.5 m/s 2 D. 当 F 增大时，小滑块的加速度一定增大 √ √ 解析　 长木板与小滑块相对静止时，对整体分析 ， 由 牛顿第二定律有： F ＝ ( M ＋ m ) a ， 当 F ＝ 6 N 时，此时两物体具有共同的最大加速度，代入数据解得： M ＋ m ＝ 3 kg ， 当 F 大于 6 N 时，对长木板，根据牛顿第二定律得： F － μmg ＝ Ma ， 故 F ＝ Ma ＋ μmg ，知图线的斜率 k ＝ M ＝ 1 kg ， 则 滑块的质量为： m ＝ 2 kg ， μmg ＝ 4 N ， μ ＝ 0.2 ，故 A 正确， B 错误 ； 当 F ＝ 6.5 N 时，长木板的加速度为： a ＝ 2.5 m/s 2 ，故 C 正确 ； 动力学方法分析 “ 传送带 ” 模型 题型：选择题： 5 年 0 考 高考题型 3 1. 模型特点 传送带问题的实质是相对运动问题，这样的相对运动将直接影响摩擦力的方向 . 2 . 解题关键 (1) 理清物体与传送带间的相对运动方向及摩擦力方向是解决传送带问题的关键 . (2) 传送带问题还常常涉及临界问题，即物体与传送带达到相同速度，这时会出现摩擦力改变的临界状态，对这一临界状态进行分析往往是解题的突破口 . 例 5 　 ( 多选 )(2019· 福建泉州市 5 月第二次质检 ) 如图 6 ，一足够长的倾斜传送带顺时针匀速转动 . 一小滑块以某初速度沿传送带向下运动，滑块与传送带间的动摩擦因数恒定，则其速度 v 随时间 t 变化的图象可能是 图 6 √ √ 解析　 设传送带倾角为 θ ，动摩擦因数为 μ ，若 mg sin θ > μmg cos θ ，合力沿传送带向下，小滑块向下匀加速运动 ； 若 mg sin θ ＝ μmg cos θ ，沿传送带方向合力为零，小滑块匀速下滑 ； 若 mg sin θ < μmg cos θ ，小滑块所受合力沿传送带向上，小滑块做匀减速运动，当减速为零时，开始反向加速，当加速到与传送带速度相同时，因为最大静摩擦力大于小滑块重力沿传送带向下的分力，故小滑块随传送带做匀速运动， A 、 D 错误， B 、 C 正确 . 拓展训练 4 　 ( 多选 )(2019· 陕西榆林市第三次测试 ) 如图 7 所示，绷紧的水平传送带足够长，且始终以 v 1 ＝ 2 m/s 的恒定速率顺时针运行 . 初速度大小为 v 2 ＝ 3 m/s 的小墨块从与传送带等高的光滑水平地面上的 A 处滑上传送带 . 若从小墨块滑上传送带开始计时，小墨块在传送带上运动 5 s 后与传送带的速度相同，则 A. 小墨块未与传送带速度相同时，受到的摩擦力方向 水平 　 向右 B. 小墨块的加速度大小为 0.2 m/s 2 C. 小墨块在传送带上的痕迹长度为 4.5 m D. 小墨块在传送带上的痕迹长度为 12.5 m 图 7 √ √ 解析　 小墨块未与传送带速度相同时，相对传送带向左运动，受到传送带的摩擦力方向水平向右，故 A 正确； 动力学方法分析 “ 板 — 块 ” 模型 题型：选择或者计算题： 5 年 3 考 高考题型 4 1. 模型特点 “ 滑块 — 木板 ” 模型类问题中，滑动摩擦力的分析方法与 “ 传送带 ” 模型类似，但这类问题比传送带类问题更复杂，因为木板受到摩擦力的影响，往往做匀变速直线运动，解决此类问题要注意从速度、位移、时间等角度，寻找各运动过程之间的联系 . 2 . 解题关键 (1) 临界条件：要使滑块不从木板的末端掉下来的临界条件是滑块到达木板末端时的速度与木板的速度恰好相同 . (2) 问题实质： “ 板 — 块 ” 模型和 “ 传送带 ” 模型一样，本质上都是相对运动问题，要分别求出各物体对地的位移，再求相对位移 . 例 6 　 ( 2019· 湖南衡阳市联考 ( 二 )) 如图 8 所示，在水平地面上有一质量为 m 1 ＝ 1 kg 的足够长的木板，其上叠放一质量为 m 2 ＝ 2 kg 的木块，木块与木板之间的动摩擦因数 μ 1 ＝ 0.3 ，木板与地面间的动摩擦因数 μ 2 ＝ 0.1. 设最大静摩擦力和滑动摩擦力相等 . 现给木块施加随时间 t 增大的水平拉力 F ＝ 3 t (N) ，取重力加速度 g ＝ 10 m/s 2 . (1) 求木块和木板保持相对静止的时间 t 1 ； 图 8 答案　 见解析 解析　 当 F < μ 2 ( m 1 ＋ m 2 ) g ＝ 3 N 时， 此时 F < μ 1 m 2 g ＝ 6 N ， 木块和木板都没有被拉动，处于静止状态 . 当木块和木板一起运动时， 对 m 1 ： F fmax － μ 2 ( m 1 ＋ m 2 ) g ＝ m 1 a max ， F fmax ＝ μ 1 m 2 g 解得： a max ＝ 3 m/s 2 对 m 1 和 m 2 整体有： F max － μ 2 ( m 1 ＋ m 2 ) g ＝ ( m 1 ＋ m 2 ) a max 解得 F max ＝ 12 N 由 F max ＝ 3 t 1 (N) 得： t 1 ＝ 4 s (2) t ＝ 10 s 时，两物体的加速度各为多大； 答案　 见解析 解析　 t ＝ 10 s 时，木块与木板已相对运动，则有： 对 m 1 ： μ 1 m 2 g － μ 2 ( m 1 ＋ m 2 ) g ＝ m 1 a 1 解得： a 1 ＝ 3 m/s 2 对 m 2 ： F － μ 1 m 2 g ＝ m 2 a 2 F ＝ 30 N 解得： a 2 ＝ 12 m/s 2 . (3) 画出木块的加速度随时间变化的图象 .( 取水平拉力 F 的方向为正方向，只要求画图，不要求写出理由及计算过程 ) 答案　 见解析 解析　 图象 过 (1,0) ， (4,3) ， (10,12) 拓展训练 5 　 (2019· 辽宁沈阳市第一次质检 ) 如图 9 所示，一足够长的木板在粗糙水平地面上向右运动 . 某时刻速度为 v 0 ＝ 2 m /s ，此时一与木板质量相等的小滑块 ( 可视为质点 ) 以 v 1 ＝ 4 m/s 的速度从右侧滑上木板，经过 1 s 两者速度恰好相同，速度大小为 v 2 ＝ 1 m /s ，方向向左 . 取重力加速度 g ＝ 10 m/s 2 ，试求： 图 9 (1) 木板与滑块间的动摩擦因数 μ 1 ； 答案　 0.3 　 对 小滑块，设小滑块的质量为 m ， 根据 牛顿第二定律有：－ μ 1 mg ＝ ma 1 ，可以得到： μ 1 ＝ 0.3 ； (2) 木板与地面间的动摩擦因数 μ 2 ； 答案　 0.05 解析　 对 木板分析，向右减速运动过程，根据牛顿第二定律以及运动学公式可以得到 ： 向左加速运动过程，根据牛顿第二定律以及运动学公式可以得到： 而且 t 1 ＋ t 2 ＝ t ＝ 1 s 联立可以得到： μ 2 ＝ 0.05 ， t 1 ＝ 0.5 s ， t 2 ＝ 0.5 s ； (3) 从滑块滑上木板，到最终两者速度恰好相同的过程中，滑块相对木板的位移大小 . 答案　 2.75 m 则整个过程中滑块相对木板的位移大小为： Δ x ＝ x ＋ x 1 － x 2 ＝ 2.75 m. 本课结束