2017-2018学年重庆市第一中学高二下学期期末考试数学（文）试题（Word版） 10页

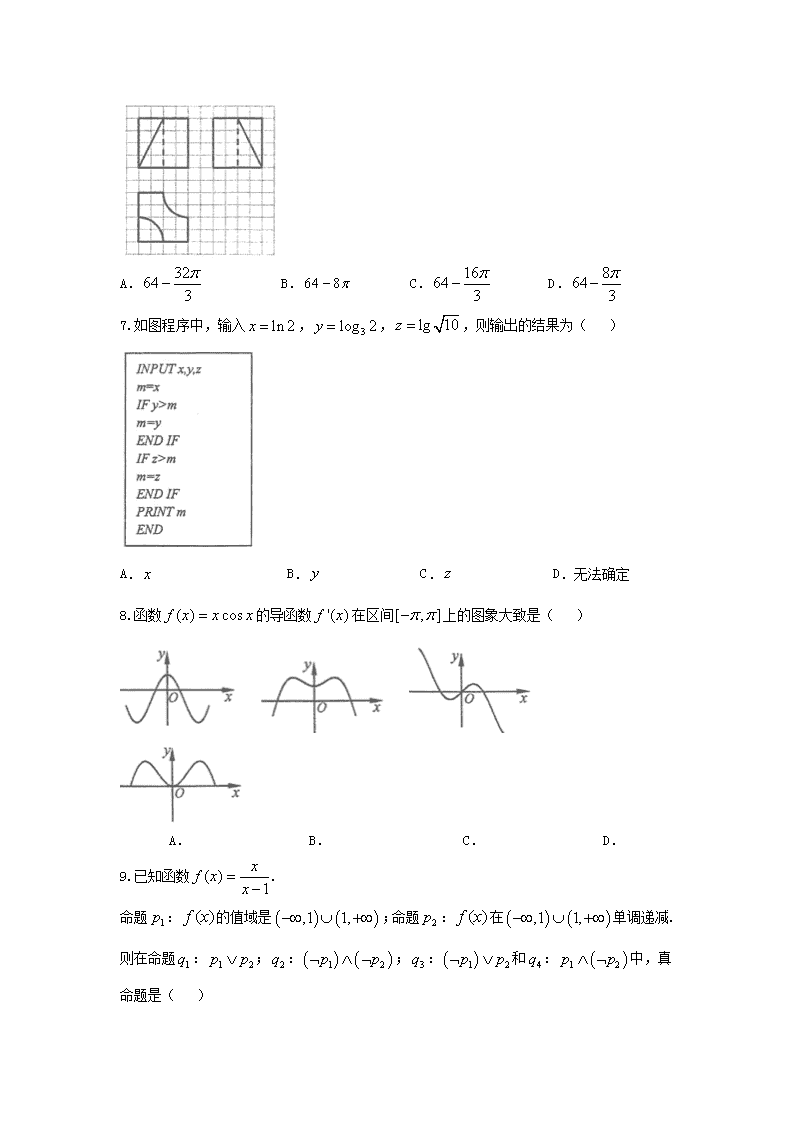
‎2017-2018学年重庆市第一中学高二下学期期末考试数学试题卷（文科）‎ 第Ⅰ卷 选择题（共60分）‎ 一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.设集合，，则（ ）‎ A． B． C． D．‎ ‎2.复数（ ）‎ A． B． C． D．‎ ‎3.已知等差数列的通项公式为，且满足，，则（ ）‎ A． B． C． D．‎ ‎4.已知函数为偶函数，且在单调递减，则的解集为（ ）‎ A． B． C． D．‎ ‎5.已知双曲线的离心率为，焦点到渐近线的距离为，则此双曲线的焦距等于（ ）‎ A． B． C． D．‎ ‎6.如图，格纸上小正方形的边长为，粗线画出的是某几何体的三视图，俯视图中的两条曲线均为圆弧，则该几何体的体积为（ ）‎ A． B． C． D．‎ ‎7.如图程序中，输入，，，则输出的结果为（ ）‎ A． B． C． D．无法确定 ‎8.函数的导函数在区间上的图象大致是（ ）‎ ‎ ‎ ‎ A． B． C． D．‎ ‎9.已知函数.‎ 命题：的值域是；命题：在单调递减.‎ 则在命题：；：；：和：中，真命题是（ ）‎ A．， B．， C．， D．，‎ ‎10.对任意实数都有，若的图象关于成中心对称，，则（ ）‎ A． B． C． D．‎ ‎11.对于实数、、，下列说法：①若，则；②若，则；③若，，则；④若且，则的最小值是，正确的个数为（ ）‎ A． B． C． D．‎ ‎12.已知函数，，若对任意的，都有成立，则实数的取值范围是（ ）‎ A． B． C． D．‎ 第Ⅱ卷 非选择题（共90分）‎ 二、填空题：本题共4小题，每小题5分，共20分.‎ ‎13.已知奇函数满足，则 ．‎ ‎14.已知曲线的一条切线为，则实数的值为 ．‎ ‎15.通常，满分为分的试卷，分为及格线.若某次满分为分的测试卷，人参加测试，将这人的卷面分数按照，，…，分组后绘制的频率分布直方图如图所示.由于及格人数较少，某位老师准备将每位学生的卷面得分采用“开方乘以取整”的方法进行换算以提高及格率（实数的取整等于不超过的最大整数），如：某位学生卷面分，则换算成分作为他的最终考试成绩，则按照这种方式，这次测试的及格率将变为 ．（结果用小数表示）‎ ‎16.已知定义在上的函数，若有零点，则实数的取值范围是 ．‎ 三、解答题：本大题共6小题，共70分.‎ ‎17.在中，角，，所对的边分别是，，，且.‎ ‎（1）求的大小；‎ ‎（2） 若，，求的面积.‎ ‎18.近年来，某地区积极践行“绿水青山就是金山银山”的绿色发展理念，年年初至年年初，该地区绿化面积（单位：平方公里）的数据如下表：‎ 年份 年份代号 绿化面积 ‎（1）求关于的线性回归方程；‎ ‎（2）利用（1）中的回归方程，预测该地区年年初的绿化面积.‎ ‎（附：回归直线的斜率与截距的最小二乘法估计公式分别为：，.其中）‎ ‎19.如图，在四棱锥中，底面是梯形，，，，.‎ ‎（1）证明：平面平面；‎ ‎（2）若与平面所成的角为，，，求点到平面的距离.‎ ‎20.已知动点到定点的距离与到定直线的距离相等.‎ ‎（1）求点的轨迹的方程；‎ ‎（2）直线交于，两点，且的面积为，求的方程.‎ ‎21.设函数，为正实数.‎ ‎（1）当时，求曲线在点处的切线方程；‎ ‎（2）求证：；‎ ‎（3）若函数有且只有个零点，求的值.‎ 选考题：请考生在22、23题中任选一题作答，如果多做，则按所做的第一题记分.‎ ‎22.选修4-4：坐标系与参数方程 在直角坐标系中，圆的普通方程为.在以坐标原点为极点，轴正半轴为极轴的极坐标系中，直线的极坐标方程为.‎ ‎（1）写出圆的参数方程和直线的直角坐标方程；‎ ‎（2）设直线与轴和轴的交点分别为、、为圆上的任意一点，求的取值范围.‎ ‎23.选修4-5：不等式选讲 已知函数，.‎ ‎（1）若对于任意，都满足，求的值；‎ ‎（2）若存在，使得成立，求实数的取值范围.‎ ‎2018年重庆一中高2019级高二下期期末考试 数学参考答案（文科）‎ 一、选择题 ‎1-5: BCDBD 6-10: CAABB 11、12：CA 二、填空题 ‎13. 14. 15. 16. ‎ 三、解答题 ‎17.，，，.‎ ‎18.（1），，，，‎ 线性回归方程为.‎ ‎（2）将年年号代入，预测绿化面积为平方公里.‎ ‎19.解：（1）证明：在中，由余弦定理得 ‎，‎ ‎∵，，‎ ‎∴，‎ ‎∴，即.‎ 又∵，，‎ ‎∴平面.‎ ‎∵平面，‎ ‎∴平面平面.‎ ‎（2）解：取的中点，连接，，‎ ‎∵，∴.‎ 由（1）知平面平面，交线为，∴平面，‎ 由，得，，，‎ ‎∵与平面所成的角为，∴，得，∴，.‎ ‎∵，∴平面，故点到平面的距离即为点到平面的距离，‎ 在三棱锥中，，‎ 即，求得，∴点到平面的距离为.‎ ‎20.解：（1）由抛物线定义可知，的轨迹方程是：.‎ ‎（2）直线的斜率显然存在，设直线：，，，‎ 由得：，‎ ‎，，‎ 由，∴，‎ ‎∴直线方程为：，所以直线恒过定点，‎ ‎∴，∴，‎ 即，∴，‎ ‎，，‎ 所以直线方程为：.‎ ‎21.解：（1）当时，，则，所以，‎ 又，所以曲线在点处的切线方程为.‎ ‎（2）因为，设函数，则，‎ 令，得，列表如下：‎ ‎+‎ ‎0‎ ‎-‎ 极大值 所以的极大值为.所以.‎ ‎（3），，‎ 令，得，因为，‎ 所以在上单调增，在上单调减.‎ 所以.‎ 设，因为函数只有个零点，而，‎ 所以是函数的唯一零点.‎ 当时，，有且只有个零点，‎ 此时，解得.‎ 下证，当时，的零点不唯一.‎ 若，则，此时，即，则.‎ 由（2）知，，又函数在以和为端点的闭区间上的图象不间断，‎ 所以在和之间存在的零点，则共有个零点，不符合题意；‎ 若，则，此时，即，则.‎ 同理可得，在和之间存在的零点，则共有个零点，不符合题意.‎ 因此，所以的值为.‎ ‎22.解：（1）圆的参数方程为（为参数）.‎ 直线的直角坐标方程为.‎ ‎（2）由直线的方程可得点，点.设点，则 ‎.‎ 由（1）知，则.‎ 因为，所以.‎ ‎23.解：（1）因为，，所以的图象关于对称.‎ 又的图象关于对称，所以，所以.‎ ‎（2）等价于.‎ 设，则.‎ 由题意，即.‎ 当时，，，所以；‎ 当时，，，所以，综上.‎