2018年四川省遂宁市高考数学一诊试卷（理科） 22页

‎2018年四川省遂宁市高考数学一诊试卷（理科）‎ ‎　‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每个小题给出的四个选项中，只有一个是符合题目要求的．‎ ‎1．（5分）已知集合A={x|﹣3＜x＜6}，B={x|2＜x＜7}，则A∩（∁RB）=（　　）‎ A．（2，6） B．（2，7） C．（﹣3，2] D．（﹣3，2）‎ ‎2．（5分）已知复数z=a+i（a∈R），若z+=4，则复数z的共轭复数=（　　）‎ A．2+i B．2﹣i C．﹣2+i D．﹣2﹣i ‎3．（5分）“”是“log2a＞log2b”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎4．（5分）已知随机变量ξ服从正态分布N（μ，σ2），若P（ξ＜2）=P（ξ＞6）=0.15，则P（2≤ξ＜4）等于（　　）‎ A．0.3 B．0.35 C．0.5 D．0.7‎ ‎5．（5分）已知α满足cos2α=，则cos（+α）cos（﹣α）=（　　）‎ A． B． C．﹣ D．﹣‎ ‎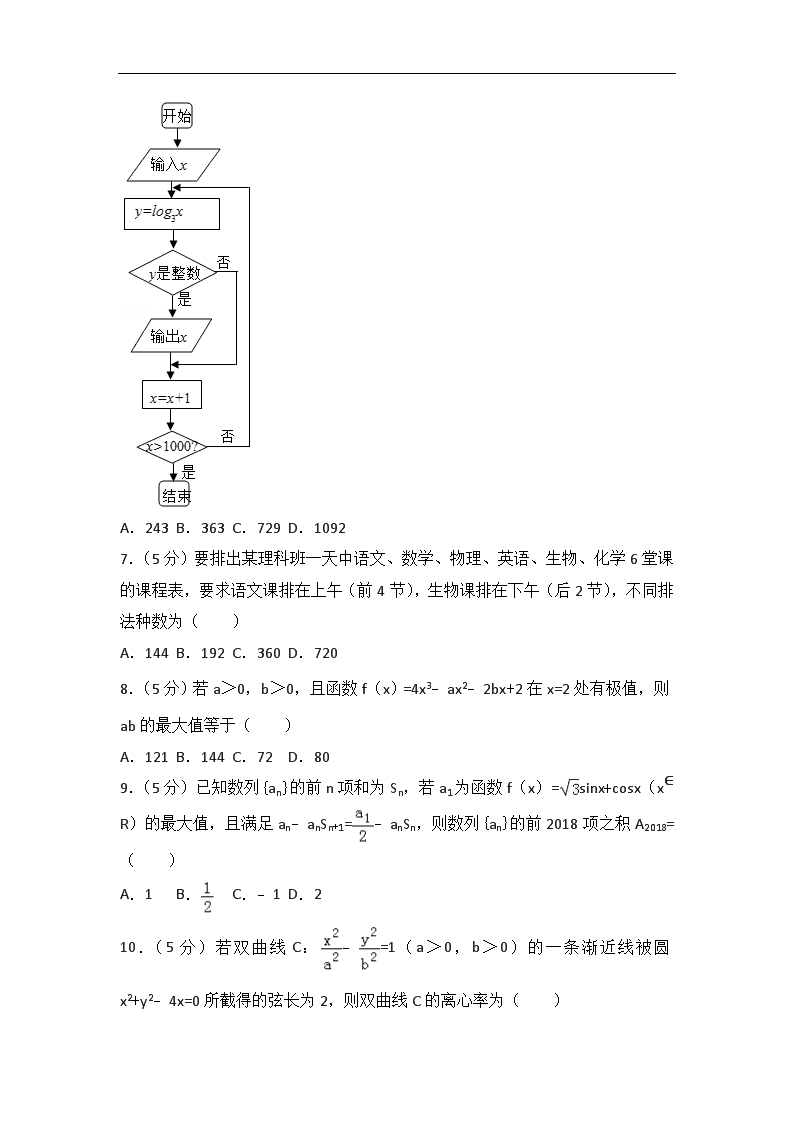6．（5分）执行如图所示的程序，若输入的x=3，则输出的所有x的值的和为（　　）‎ A．243 B．363 C．729 D．1092‎ ‎7．（5分）要排出某理科班一天中语文、数学、物理、英语、生物、化学6堂课的课程表，要求语文课排在上午（前4节），生物课排在下午（后2节），不同排法种数为（　　）‎ A．144 B．192 C．360 D．720‎ ‎8．（5分）若a＞0，b＞0，且函数f（x）=4x3﹣ax2﹣2bx+2在x=2处有极值，则ab的最大值等于（　　）‎ A．121 B．144 C．72 D．80‎ ‎9．（5分）已知数列{an}的前n项和为Sn，若a1为函数f（x）=sinx+cosx（x∈R）的最大值，且满足an﹣anSn+1=﹣anSn，则数列{an}的前2018项之积A2018=（　　）‎ A．1 B． C．﹣1 D．2‎ ‎10．（5分）若双曲线C：﹣=1（a＞0，b＞0）的一条渐近线被圆x2+y2﹣4x=0所截得的弦长为2，则双曲线C的离心率为（　　）‎ A．2 B． C． D．‎ ‎11．（5分）已知O为△ABC的外心，A为锐角且sinA=，若=α+β，则α+β的最大值为（　　）‎ A． B． C． D．‎ ‎12．（5分）定义在R上的函数f（x）满足f（﹣x）=f（x），且对任意的不相等的实数x1，x2∈[0，+∞）有＜0成立，若关于x的不等式f（2mx﹣lnx﹣3）≥2f（3）﹣f（﹣2mx+lnx+3）在x∈[1，3]上恒成立，则实数m的取值范围（　　）‎ A．[，1+] B．[，2+] C．[，2+] D．[，1+]‎ ‎　‎ 二、填空题：本大题共4个小题，每小题5分，共20分．‎ ‎13．（5分）设x，y满足约束条件，则目标函数z=2x+y的最小值是　 　．‎ ‎14．（5分）二项式（2﹣）6展开式中常数项是　 　．‎ ‎15．（5分）已知点A，B的坐标分别为（﹣1，0），（1，0）．直线AM，BM相交于点M，且它们的斜率之和是2，则点M的轨迹方程为　 　．‎ ‎16．（5分）设函数与g（x）=a2lnx+b有公共点，且在公共点处的切线方程相同，则实数b的最大值为　 　．‎ ‎　‎ 三、解答题：本大题共70分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（12分）已知数列{an}的前n项和为Sn，向量=（Sn，2），满足条件⊥‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）设cn=，求数列{cn}的前n项和Tn．‎ ‎18．（12分）已知函数，在△ABC中，角A，B，C的对边分别为a，b，c ‎（1）当x∈[0，]时，求函数f（x）的取值范围；‎ ‎（2）若对任意的x∈R都有f（x）≤f（A），c=2b=4，点D是边BC的中点，求的值．‎ ‎19．（12分）心理学家分析发现视觉和空间能力与性别有关，某数学兴趣小组为了验证这个结论，从兴趣小组中用分层抽样的方法抽取50名同学（男30，女20），给所选的同学几何题和代数题各一题，让各位同学自由选择一题进行解答，选题情况如表（单位：人）‎ 几何体 代数题 总计 男同学 ‎22‎ ‎8‎ ‎30‎ 女同学 ‎8‎ ‎12‎ ‎20‎ 总计 ‎30‎ ‎20‎ ‎50‎ ‎（1）能否据此判断有97%的把握认为视觉和空间能力与性别有关 ‎（2）经过多次测试后，甲每次解答一道几何题所用的时间在5﹣7分钟，乙每次解答一道几何题所用的时间在6﹣8分钟，现甲乙解同一道几何题，求乙比甲先解答完成的概率 ‎（3）现从选择做几何题的8名女生中任意抽取两人对她们的大题情况进行全程研究，记甲、乙两女生被抽到的人数为X，求X的分布列及数学期E（X）‎ 附表及公式 P（k2≥k0）‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.10‎ ‎0.005‎ ‎0.001‎ k0‎ ‎2.072‎ ‎2.706‎ ‎3.481‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ k2=．‎ ‎20．（12分）设椭圆+=1（a＞b＞0）的离心率e=‎ ‎，左焦点为F，右顶点为A，过点F的直线交椭圆于E，H两点，若直线EH垂直于x轴时，有|EH|=‎ ‎（1）求椭圆的方程；‎ ‎（2）设直线l：x=﹣1上两点P，Q关于x轴对称，直线AP与椭圆相交于点B（B异于点A），直线BQ与x轴相交于点D．若△APD的面积为，求直线AP的方程．‎ ‎21．（12分）已知函数f（x）=ex+px﹣﹣2lnx ‎（1）若p=2，求曲线y=f（x）在点（1，f（1））处的切线；‎ ‎（2）若函数F（x）=f（x）﹣ex在其定义域内为增函数，求正实数p的取值范围；‎ ‎（3）设函数g（x）=ex+，若在[1，e]上至少存在一点x0，使得f（x0）＞g（x0）成立，求实数p的取值范围．‎ ‎　‎ 请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]‎ ‎22．（10分）已知直线l的参数方程为（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ=4cos（θ﹣）．‎ ‎（1）求圆C的直角坐标方程；‎ ‎（2）若P（x，y）是直线l与圆面的公共点，求x+y的取值范围．‎ ‎23．已知函数f（x）=|1﹣x﹣a|+|2a﹣x|‎ ‎（1）若f（1）＜3，求实数a的取值范围；‎ ‎（2）若a≥，x∈R，判断f（x）与1的大小关系并证明．‎ ‎　‎ ‎2018年四川省遂宁市高考数学一诊试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每个小题给出的四个选项中，只有一个是符合题目要求的．‎ ‎1．（5分）已知集合A={x|﹣3＜x＜6}，B={x|2＜x＜7}，则A∩（∁RB）=（　　）‎ A．（2，6） B．（2，7） C．（﹣3，2] D．（﹣3，2）‎ ‎【解答】解：∵B={x|2＜x＜7}，‎ ‎∴∁RB）={x|x≤2或x≥7}，‎ ‎∴A∩（∁RB）=（﹣3，2]，‎ 故选：C．‎ ‎　‎ ‎2．（5分）已知复数z=a+i（a∈R），若z+=4，则复数z的共轭复数=（　　）‎ A．2+i B．2﹣i C．﹣2+i D．﹣2﹣i ‎【解答】解：∵z=a+i，‎ ‎∴z+=2a=4，得a=2．‎ ‎∴复数z的共轭复数=2﹣i．‎ 故选：B．‎ ‎　‎ ‎3．（5分）“”是“log2a＞log2b”的（　　）‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎【解答】解：“”⇔a＞b，‎ ‎“log2a＞log2b”⇔a＞b＞0．‎ ‎∴“”是“log2a＞log2b”的必要不充分条件．‎ 故选：B．‎ ‎　‎ ‎4．（5分）已知随机变量ξ服从正态分布N（μ，σ2），若P（ξ＜2）=P（ξ＞6）=0.15，则P（2≤ξ＜4）等于（　　）‎ A．0.3 B．0.35 C．0.5 D．0.7‎ ‎【解答】解：由题意可得，‎ 故选：B．‎ ‎　‎ ‎5．（5分）已知α满足cos2α=，则cos（+α）cos（﹣α）=（　　）‎ A． B． C．﹣ D．﹣‎ ‎【解答】解：∵α满足cos2α=，则cos（+α）cos（﹣α）=cos（+α）cos[﹣（+α）]‎ ‎=cos（+α）sin（+α）=sin（+2α）=cos2α=，‎ 故选：A．‎ ‎　‎ ‎6．（5分）执行如图所示的程序，若输入的x=3，则输出的所有x的值的和为（　　）‎ A．243 B．363 C．729 D．1092‎ ‎【解答】解：模拟程序的运行可得：当x=3时，y是整数；‎ 当x=32时，y是整数；‎ 依此类推可知当x=3n（n∈N*）时，y是整数，‎ 则由x=3n≥1000，得n≥7，‎ 所以输出的所有x的值为3，9，27，81，243，729，其和为1092，‎ 故选：D．‎ ‎　‎ ‎7．（5分）要排出某理科班一天中语文、数学、物理、英语、生物、化学6堂课的课程表，要求语文课排在上午（前4节），生物课排在下午（后2节），不同排法种数为（　　）‎ A．144 B．192 C．360 D．720‎ ‎【解答】解：根据题意，分2步进行分析：‎ ‎①，要求数学课排在上午（前4节），生物课排在下午（后2节），‎ 则数学课有4种排法，生物课有2种排法，‎ 故这两门课有4×2=8种排法；‎ ‎②，将剩下的4门课全排列，安排在其他四节课位置，有A44=24种排法，‎ 则共有8×24=192种排法，‎ 故选：B．‎ ‎　‎ ‎8．（5分）若a＞0，b＞0，且函数f（x）=4x3﹣ax2﹣2bx+2在x=2处有极值，则ab的最大值等于（　　）‎ A．121 B．144 C．72 D．80‎ ‎【解答】解：由题意，求导函数f′（x）=12x2﹣2ax﹣2b，‎ ‎∵在x=2处有极值，‎ ‎2a+b=24，‎ ‎∵a＞0，b＞0，‎ ‎∴2ab≤（）2=144，当且仅当2a=b时取等号，‎ 所以ab的最大值等于72，‎ 故选：C．‎ ‎　‎ ‎9．（5分）已知数列{an}的前n项和为Sn，若a1为函数f（x）=sinx+cosx（x∈R）的最大值，且满足an﹣anSn+1=﹣anSn，则数列{an}的前2018项之积A2018=（　　）‎ A．1 B． C．﹣1 D．2‎ ‎【解答】解：函数f（x）=sinx+cosx=2sin（x+），‎ 当x=2kπ+，k∈Z时，f（x）取得最大值2，‎ 则a1=2，‎ 由an﹣anSn+1=﹣anSn=1﹣anSn，‎ 即为an=anSn+1﹣anSn+1，‎ 即有an+1==1﹣，‎ an+2=1﹣=，‎ an+3=1﹣=an，‎ 则数列{an}为周期为3的数列，‎ 且a1=2，a2=，a3=﹣1，‎ 则一个周期的乘积为﹣1，‎ 由于2018=3×672+2，‎ 则数列{an}的前2018项之积A2018=1×2×=1．‎ 故选A．‎ ‎　‎ ‎10．（5分）若双曲线C：﹣=1（a＞0，b＞0）的一条渐近线被圆x2+y2﹣4x=0所截得的弦长为2，则双曲线C的离心率为（　　）‎ A．2 B． C． D．‎ ‎【解答】解：双曲线C：﹣=1（a＞0，b＞0）的一条渐近线不妨为：bx+ay=0，‎ 圆x2+y2﹣4x=0即为（x﹣2）2+y2=4的圆心（2，0），半径为2，‎ 双曲线的一条渐近线被圆x2+y2﹣4x=0所截得的弦长为2，‎ 可得圆心到直线的距离为：=，‎ 解得：=3，‎ 由e=，‎ 可得e2=4，即e=2．‎ 故选A．‎ ‎　‎ ‎11．（5分）已知O为△ABC的外心，A为锐角且sinA=，若=α+β，则α+β的最大值为（　　）‎ A． B． C． D．‎ ‎【解答】解：如图所示，以BC边所在直线为x轴，‎ BC边的垂直平分线为y轴建立直角坐标系（D为BC边的中点）．‎ 由外接圆的性质可得∠BOD=∠COD=∠BAC．‎ 由A为锐角且sinA=，‎ 不妨设外接圆的半径R=3．则OA=OB=OC=3．‎ ‎∵cos∠COD==cosA=，‎ ‎∴OD=1，DC==2．‎ ‎∴B（﹣2，0），C（2，0），O（0，1），A（m，n），‎ 则△ABC外接圆的方程为：x2+（y﹣1）2=9．（*）‎ ‎∵=α+β，‎ ‎∴（﹣m，1﹣n）=α（﹣2﹣m，﹣n）+β（2﹣m，﹣n），‎ ‎∴，‎ ‎∵α+β≠1时，否则=α，由图可知是不可能的．‎ ‎∴可化为，‎ 代入（*）可得+=9，‎ 化为18（α+β）=9+32αβ，‎ 利用重要不等式可得18（α+β）≤9+32（）2，‎ 化为8（α+β）2﹣18（α+β）+9≥0，‎ 解得α+β≤或α+β≥．‎ 又α+β＜1，故α+β≥应舍去．‎ ‎∴α+β≤，‎ 则α+β的最大值为，‎ 故选：D．‎ ‎　‎ ‎12．（5分）定义在R上的函数f（x）满足f（﹣x）=f（x），且对任意的不相等的实数x1，x2∈[0，+∞）有＜0成立，若关于x的不等式f（2mx﹣lnx﹣3）≥2f（3）﹣f（﹣2mx+lnx+3）在x∈[1，3]上恒成立，则实数m的取值范围（　　）‎ A．[，1+] B．[，2+] C．[，2+] D．[，1+]‎ ‎【解答】解：∴定义在R上的函数f（x）的图象关于y轴对称，‎ ‎∴函数f（x）为偶函数，‎ ‎∵函数数f（x）在[0，+∞）上递减，‎ ‎∴f（x）在（﹣∞，0）上单调递增，‎ 若不等式f（2mx﹣lnx﹣3）≥2f（3）﹣f（﹣2mx+lnx+3）对x∈[1，3]恒成立，‎ 即f（2mx﹣lnx﹣3）≥f（3）对x∈[1，3]恒成立．‎ ‎∴﹣3≤2mx﹣lnx﹣3≤3对x∈[1，3]恒成立，‎ 即0≤2mx﹣lnx≤6对x∈[1，3]恒成立，即2m≥且2m≤对x∈[1，3]‎ 恒成立．‎ 令g（x）=，则 g′（x）=，在[1，e）上递增，（e，3]上递减，‎ ‎∴g（x）max=．‎ 令h（x）=，h′（x）=＜0，在[1，3]上递减，‎ ‎∴h（x）min=．‎ 综上所述，m∈[，]．‎ 故选D．‎ ‎　‎ 二、填空题：本大题共4个小题，每小题5分，共20分．‎ ‎13．（5分）设x，y满足约束条件，则目标函数z=2x+y的最小值是　﹣15　．‎ ‎【解答】解：x，y满足约束条件的可行域如图：‎ 在坐标系中画出可行域△ABC，A（﹣6，﹣3），B（0，1），C（6，﹣3），‎ 由图可知，当x=﹣6，y=﹣3时，则目标函数z=2x+y的最小，最小值为﹣15．‎ 故答案为：﹣15．‎ ‎　‎ ‎14．（5分）二项式（2﹣）6展开式中常数项是　﹣160　．‎ ‎【解答】解：因为=20×8×（﹣1）=﹣160．‎ 所以展开式中常数项是﹣160．‎ 故答案为：﹣160．‎ ‎　‎ ‎15．（5分）已知点A，B的坐标分别为（﹣1，0），（1，0）．直线AM，BM相交于点M，且它们的斜率之和是2，则点M的轨迹方程为　x2﹣xy﹣1=0（x≠±1）　．‎ ‎【解答】解：设M（x，y），∵AM，BM的斜率存在，∴x≠±1，‎ 又∵kAM=，kBM=，‎ ‎∴由kAM+kBM=2得：•=0，‎ 整理得：x2﹣xy﹣1=0，‎ ‎∴点M的轨迹方程为：x2﹣xy﹣1=0（x≠±1）．‎ 故答案为：x2﹣xy﹣1=0（x≠±1）‎ ‎　‎ ‎16．（5分）设函数与g（x）=a2lnx+b有公共点，且在公共点处的切线方程相同，则实数b的最大值为　　．‎ ‎【解答】解：设公共点坐标为（x0，y0），则，‎ 所以有f'（x0）=g'（x0），即，解出x0=a（舍去），‎ 又y0=f（x0）=g（x0），所以有，‎ 故，‎ 所以有，对b求导有b'=﹣2a（1+lna），‎ 故b关于a的函数在为增函数，在为减函数，‎ 所以当时b有最大值．‎ 故答案为：．‎ ‎　‎ 三、解答题：本大题共70分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（12分）已知数列{an}的前n项和为Sn，向量=（Sn，2），满足条件⊥‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）设cn=，求数列{cn}的前n项和Tn．‎ ‎【解答】解：（1）∵⊥，‎ ‎∴•=Sn+2﹣2n+1=0，‎ ‎∴Sn=2n+1﹣2，‎ 当n≥2时，an=Sn﹣Sn﹣1=2n，‎ 当n=1时，a1=S1=2满足上式，‎ ‎∴an=2n，‎ ‎（2）∵cn==，‎ ‎∴，两边同乘，‎ 得，两式相减得：‎ ‎，‎ ‎∴．‎ ‎　‎ ‎18．（12分）已知函数，在△ABC中，角A，B，C的对边分别为a，b，c ‎（1）当x∈[0，]时，求函数f（x）的取值范围；‎ ‎（2）若对任意的x∈R都有f（x）≤f（A），c=2b=4，点D是边BC的中点，求的值．‎ ‎【解答】解：（1）当x∈[0，]时，2x﹣∈[﹣，]，‎ sin（2x﹣）∈[﹣，1]，‎ 所以函数的取值范围是[0，3]； ‎ ‎（2）由对任意的x∈R，都有f（x）≤f（A），得 ‎2A﹣=2kπ+，k∈Z，解得A=kπ+，k∈Z，‎ 又∵A∈（0，π）∴，‎ ‎∵‎ ‎=（c2+b2+2bccosA）=（c2+b2+bc）=×（16+4+8）=7，‎ 所以．‎ ‎　‎ ‎19．（12分）心理学家分析发现视觉和空间能力与性别有关，某数学兴趣小组为了验证这个结论，从兴趣小组中用分层抽样的方法抽取50名同学（男30，女20），给所选的同学几何题和代数题各一题，让各位同学自由选择一题进行解答，选题情况如表（单位：人）‎ 几何体 代数题 总计 男同学 ‎22‎ ‎8‎ ‎30‎ 女同学 ‎8‎ ‎12‎ ‎20‎ 总计 ‎30‎ ‎20‎ ‎50‎ ‎（1）能否据此判断有97%的把握认为视觉和空间能力与性别有关 ‎（2）经过多次测试后，甲每次解答一道几何题所用的时间在5﹣7分钟，乙每次解答一道几何题所用的时间在6﹣8分钟，现甲乙解同一道几何题，求乙比甲先解答完成的概率 ‎（3）现从选择做几何题的8名女生中任意抽取两人对她们的大题情况进行全程研究，记甲、乙两女生被抽到的人数为X，求X的分布列及数学期E（X）‎ 附表及公式 P（k2≥k0）‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎0.10‎ ‎0.005‎ ‎0.001‎ k0‎ ‎2.072‎ ‎2.706‎ ‎3.481‎ ‎5.024‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ k2=．‎ ‎【解答】解：（1）由表中数据，得：‎ k2==，‎ ‎∴据此判断有97%的把握认为视觉和空间能力与性别有关．‎ ‎（2）设甲、乙解答同一道题的时间分别为x，y分钟，‎ 则基本事件满足区域为，如图所示：‎ 设事件A为“乙比甲先做完此题”，则满足的区域还要满足x＞y，‎ ‎∴由几何概型得乙比甲先解答完成的概率P（A）==．‎ ‎（3）由题意知在8名女生中任意抽取2人，抽取方法有种，‎ 其中甲、乙两人没有一个人被抽取有种，‎ 恰有一人被抽到有种，两人都被抽到有种，‎ ‎∴X的可能取值有0，1，2，‎ P（X=0）=，P（X=1）=，P（X=2）=，‎ ‎∴X的分布列为：‎ ‎ X ‎ 0‎ ‎ 1‎ ‎ 2‎ ‎ P ‎ ‎ ‎ ‎ ‎ ‎ E（X）==．‎ ‎　‎ ‎20．（12分）设椭圆+=1（a＞b＞0）的离心率e=，左焦点为F，右顶点为A，过点F的直线交椭圆于E，H两点，若直线EH垂直于x轴时，有|EH|=‎ ‎（1）求椭圆的方程；‎ ‎（2）设直线l：x=﹣1上两点P，Q关于x轴对称，直线AP与椭圆相交于点B（B异于点A），直线BQ与x轴相交于点D．若△APD的面积为，求直线AP的方程．‎ ‎【解答】解：（1）设F（﹣c，0）（c＞0），‎ ‎∵e=，∴a=2c，又由|EH|=，得，‎ 且a2=b2+c2，解得，‎ 因此椭圆的方程为：；‎ ‎（2）设直线AP的方程为x=my+1（m≠0），‎ 与直线l的方程x=﹣1联立，可得点P（﹣1，﹣），故Q（﹣1，）．‎ 将x=my+1与联立，消去x，整理得（3m2+4）y2+6my=0，‎ 解得y=0，或y=．‎ 由点B异于点A，‎ 可得点B（）．‎ 由Q（﹣1，），可得直线BQ的方程为，‎ 令y=0，解得，故D（）．‎ ‎∴|AD|=．‎ 又∵△APD的面积为，故，‎ 整理得，解得|m|=，‎ ‎∴m=．‎ ‎∴直线AP的方程为，或3x﹣﹣3=0．‎ ‎　‎ ‎21．（12分）已知函数f（x）=ex+px﹣﹣2lnx ‎（1）若p=2，求曲线y=f（x）在点（1，f（1））处的切线；‎ ‎（2）若函数F（x）=f（x）﹣ex在其定义域内为增函数，求正实数p的取值范围；‎ ‎（3）设函数g（x）=ex+，若在[1，e]上至少存在一点x0，使得f（x0）＞g（x0）成立，求实数p的取值范围．‎ ‎【解答】解：因为函数f（x）=ex+px﹣﹣2lnx，‎ ‎（1）当p=2时，f（x）=ex+2x﹣﹣2lnx，f（1）=e，‎ 又，∴f′（1）=e+2，‎ 则曲线y=f（x）在点（1，f（1））处的切线方程为：y﹣e=（e+2）（x﹣1），‎ 即（e+2）x﹣y﹣2=0；‎ ‎（2）F（x）=f（x）﹣ex=px﹣，，‎ 由F（x）在定义域（0，+∞）内为增函数，∴F'（x）≥0在（0，+∞）上恒成立，‎ ‎∴px2﹣2x+p≥0，即对任意x＞0恒成立，‎ 设，‎ 可知h（x）在（0，1）上单调递增，在（1，+∞）上单调递减，‎ 则h（x）max=h（1）=1，∴p≥h（1）=1，即p∈[1，+∞）；‎ ‎（3）设函数φ（x）=f（x）﹣g（x）=px﹣，x∈[1，e]，‎ 则原问题⇔在[1，e]上至少存在一点x0，使得φ（x0）＞0⇔φ（x）max＞0（x∈[1，e]）．‎ ‎，‎ 当p=0时，，则φ（x）在x∈[1，e]上单调递增，φ（x）max=φ（e）=﹣4＜0，（舍）；‎ 当p＜0时，φ（x）=p（x﹣）﹣，‎ ‎∵x∈[1，e]，∴x﹣≥0，＞0，lnx＞0，则φ（x）＜0，（舍）；‎ 当p＞0时，，‎ 则φ（x）在x∈[1，e]上单调递增，φ（x）max=φ（e）=pe﹣＞0，‎ 整理得p＞，‎ 综上，p∈（）．‎ ‎　‎ 请考生在第22、23两题中任选一题作答，如果多做，则按所做的第一题计分．[选修4-4：坐标系与参数方程]‎ ‎22．（10分）已知直线l的参数方程为（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ=4cos（θ﹣）．‎ ‎（1）求圆C的直角坐标方程；‎ ‎（2）若P（x，y）是直线l与圆面的公共点，求x+y的取值范围．‎ ‎【解答】（本小题满分10分）‎ 解：（1）∵圆C的极坐标方程为ρ=4cos（θ﹣），‎ ‎∴，‎ 又∵ρ2=x2+y2，x=ρcosθ，y=ρsinθ，…（5分）‎ ‎∴，‎ ‎∴圆C的普通方程为=0．‎ ‎（2）设z=，‎ 圆C的方程=0．即（x+1）2+（y﹣）2=4，‎ ‎∴圆C的圆心是C（﹣1，），半径r=2，‎ 将直线l的参数方程为（t为参数）代入z=，得z=﹣t，‎ 又∵直线l过C（﹣1，），圆C的半径是2，‎ ‎∴﹣2≤t≤2，∴﹣2≤﹣t≤2，即的取值范围是[﹣2，2]．…（10分）‎ ‎　‎ ‎23．已知函数f（x）=|1﹣x﹣a|+|2a﹣x|‎ ‎（1）若f（1）＜3，求实数a的取值范围；‎ ‎（2）若a≥，x∈R，判断f（x）与1的大小关系并证明．‎ ‎【解答】解：（1）因为f（1）＜3，所以|a|+|1﹣2a|＜3，‎ ‎①当a≤0时，得﹣a+（1﹣2a）＜3，解得：a＞﹣，所以﹣＜a≤0；‎ ‎②当0＜a＜时，得a+（1﹣2a）＜3，解得a＞﹣2，所以0＜a＜；‎ ‎③当a≥时，得a﹣（1﹣2a）＜3，解得：a＜，‎ 所以≤a＜；‎ 综上所述，实数a的取值范围是（﹣，）．…（5分）‎ ‎（2）f（x）≥1，因为a≥，‎ 所以f（x）=|1﹣x﹣a|+|2a﹣x|≥|（1﹣x﹣a）﹣（2a﹣x）|=|1﹣3a|=3a﹣1≥1…（10分）‎ ‎　‎