2017年高三压轴卷全国卷（三）数学（文）试题（PDF版） 4页

２０１７ 年高三年级压轴题 　 文科数学全国卷(三) 第Ⅰ卷(选择题 　 共 ６０ 分) 一、选择题:本题共 １２ 小题,每小题 ５ 分,在每小题给出的四个选项中,只有一项是符合题目要求的． １．已知集合 A＝{(x,y)|y＝x＋１},B＝{(x,y)|y＝３－２x},则 A∩B＝ (　　) A． ２ ３,５ ３ æ è ç ö ø ÷{ } B． ２ ３,５ ３ æ è ç ö ø ÷ C． ２ ３,５ ３ { } D． ２ ３,５ ３ æ è ç ö ø ÷ , －２ ３,－５ ３ æ è ç ö ø ÷{ } ２．若z＝ １ １－i－i,则 |z|＝ (　　) A．１ ２ B．２ ２ C．－１ ２ ＋１ ２ i D．１ ２ ＋１ ２ i ３．“m＞n＞０”是“曲线 mx２＋ny２＝１ 为焦点在x 轴上的椭圆”的 (　　) A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 ４．某同学在研究性学习中,收集到某制药厂今年前 ５ 个月甲胶囊生产产量(单位:万盒)的数据如下表所示: x(月份) １ ２ ３ ４ ５ y(万盒) ５ ５ ６ ６ ８ 若x,y 线性相关,线性回归方程为^y＝０．７x＋^a,估计该制药厂 ６ 月份生产甲胶囊产量为 (　　) A．８．１ 万盒 B．８．２ 万盒 C．８．９ 万盒 D．８．６ 万盒 ５．tan７０°cos１０°＋ ３sin１０°tan７０°－２sin５０°＝ (　　) A．－１ ２ B．１ ２ C．－２ D．２ 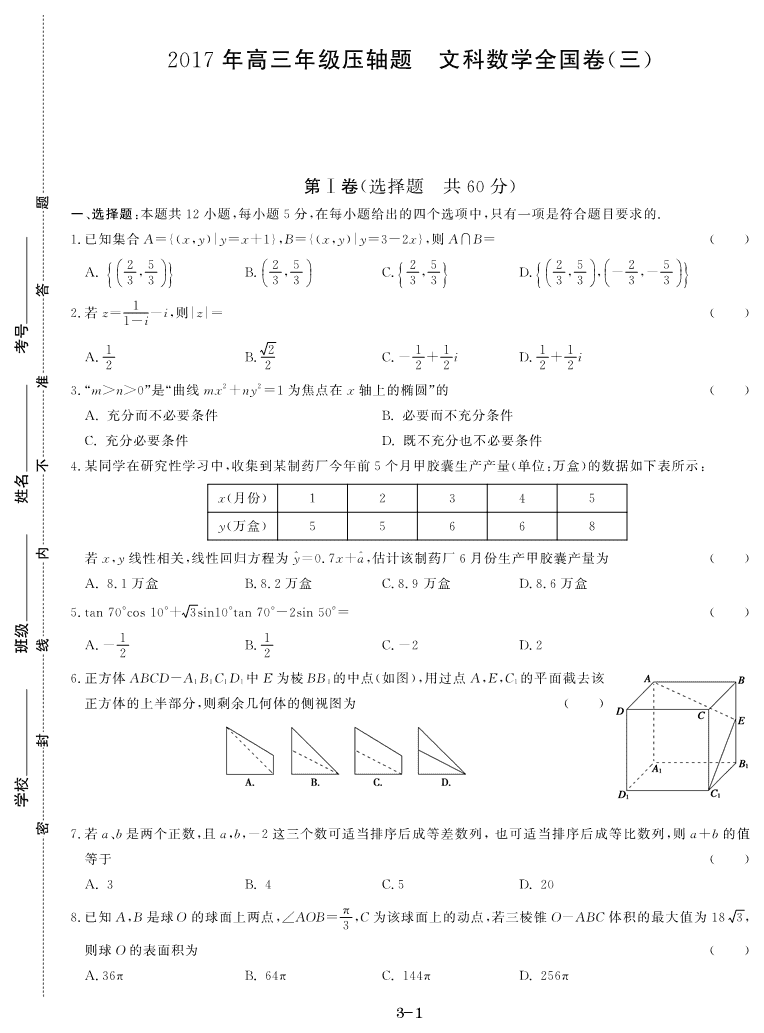６．正方体 ABCD－A１B１C１D１ 中E 为棱BB１ 的中点(如图),用过点 A,E,C１ 的平面截去该 正方体的上半部分,则剩余几何体的侧视图为 (　　) ７．若a、b是两个正数,且a,b,－２ 这三个数可适当排序后成等差数列,也可适当排序后成等比数列,则a＋b的值 等于 (　　) A．３ B．４ C．５ D．２０ ８．已知 A,B 是球O 的球面上两点,∠AOB＝π ３,C 为该球面上的动点,若三棱锥O－ABC 体积的最大值为 １８ ３, 则球O 的表面积为 (　　) A．３６π B．６４π C．１４４π D．２５６π １－３ ９．已知 O 为正 △ABC 内的一点,且满足OA→＋λOB→＋(１＋λ)OC→＝０,若 △OAB 的面积与 △OBC 的面积的比值为 ３, 则λ的值为 (　　) A．１ ２ B．５ ２ C．２ D．３ １０．右边程序框图的算法思路源于我国古代数学名著«九章算术»中的“更相减 损术”．执行该程序框图,若输入a,b分别为 ２８,１８,则输出的a＝ (　　) A．０ B．２ C．４ D．１４ １１．函数y＝sin ２x－π ３ æ è ç ö ø ÷与y＝cos２x＋２π ３ æ è ç ö ø ÷的图像关于直线x＝a 对称,则a 可能是 (　　) A．π ２４ B．π １２ C．π ８ D．１１π ２４ １２．定义:如果函数f(x)在[a,b]上存在x１,x２(a＜x１＜x２＜b)满足f′(x１)＝f(b)－f(a)b－a ,f′(x２)＝f(b)－f(a)b－a , 则称函数f(x)是[a,b]上的“双中值函数”,已知函数f(x)＝２x３－x２＋m 是[０,２a]上“双中值函数”,则实数a 的取值范围是 (　　) A． １ ８,１ ４ æ è ç ö ø ÷ B． １ １２,１ ４ æ è ç ö ø ÷ C． １ １２,１ ８ æ è ç ö ø ÷ D． １ ８,１ æ è ç ö ø ÷ 第Ⅱ卷(非选择题 　 共 ９０ 分) 本卷包括必考题和选考题两部分．第 １３~２１ 题为必考题,每个试题考生都必须作答．第 ２２~２３ 题为选考题,考生 根据要求作答． 二、填空题:本题共 ４ 小题,每小题 ５ 分． １３．若圆(x－ ３) ２＋(y－１)２＝３ 与双曲线x２ a２ －y２ b２ ＝１(a＞０,b＞０)的一条渐近线相切,则此双曲线的离心率为 　　 　　． １４．设数列 an{ }中,a１＝３,an＝an－１＋３ n (n∈N∗ ,n≥２),则an＝　　　　． １５．设 m＞１,变量x,y 在约束条件 y≥x y≤mx x＋y≤１ ì î í ïï ïï 下,目标函数z＝x＋my 最大值为 ２,则 m＝　　　　． １６．已知数列{an}的前n项和为Sn,满足Sn＝(－１) nan＋１ ２ n ,{Sn}的前n项和为Tn,则T２０１６ ＝　　　　． 三、解答题:解答应写出文字说明,证明过程或演算步骤． １７．(本小题满分 １２ 分) 已知向量 m＝ ３sin x ４,１ æ è ç ö ø ÷ ,n＝ cos x ４,cos ２ x ４ æ è ç ö ø ÷ ,记f(x)＝mŰn． (１)若f(x)＝１,求 cosx＋π ３ æ è ç ö ø ÷的值; (２)在锐角 △ABC 中,角 A,B,C 的对边分别是a,b,c,且满足(２a－c)cosB＝bcosC,求f(２A)的取值范围． ２－３ １８．(本小题满分 １２ 分) 如图所示的几何体QPABCD 为一简单组合体,在底面 ABCD 中,∠DAB＝６０°,AD⊥DC, AB⊥BC,QD⊥ 平面 ABCD,PA∥QD,PA＝１,AD＝AB＝QD＝２． (１)求证:平面PAB⊥ 平面QBC; (２)求该组合体QPABCD 的体积． １９．(本小题满分 １２ 分) 某校高三文科 ５００ 名学生参加了 １ 月份的模拟考试,学校为了了解高三文科学生的数学、语文情况,利用随机 数表法从中抽取 １００ 名学生的成绩进行统计分析,抽出的 １００ 名学生的数学、语文成绩如下表: 　 语文 数学 优 良 及格 优 ８ m ９ 良 ９ n １１ 及格 ８ ９ １１ (１)将学生编号为:００１,００２,００３,．．．．．．４９９,５００,若从第 ５ 行第 ５ 列的数开始右读,请你依次写出最先抽出的 ５ 个人的编号(下面是摘自随机数表的第四行至第七行) １２　５６　８５　９９　２６　９６　９６　６８　２７　３１　０５　０３　７２　９３　１５　５７　１２　１０　１４　２１　８８　２６　４９　８１　７６ ５５　５９　５６　３５　６４　３８　５４　８２　４６　２２　３１　６２　４３　０９　９０　０６　１８　４４　３２　５３　２３　８３　０１　３０　３０ １６　２２　７７　９４　３９　４９　５４　４３　５４　８２　１７　３７　９３　２３　７８　８７　３５　２０　９６　４３　８４　２６　３４　９１　６４ ８４　４２　１７　５３　３１　５７　２４　５５　０６　８８　７７　０４　７４　４７　６７　２１　７６　３３　５０　２５　８３　９２　１２　０６　７６ (２)若数学优秀率为 ３５％,求 m,n的值; (３)在语文成绩为良的学生中,已知 m≥１３,n≥１１,求数学成绩“优”比“良”的人数少的概率． ２０．(本小题满分 １２ 分) 已知椭圆C: x２ a２ ＋y２ b２ ＝１ a＞b＞０ ( ) 和圆 D:x２ ＋y２ ＝b２ 分别与射线y＝x x≥０ ( ) 交于 A,B 两点,且 OA ＝ ２ １０ ５ ,OB ＝２ １０ ５ ． (１)求椭圆C 的方程; (２)若不经过原点O 且斜率为k 的直线l与椭圆交于 M ,N 两点,且S△OMN ＝１,证明:线段 MN 中点P x０,y０ ( ) 的坐标满足x２ ０＋４y２ ０＝２． ３－３ ２１．(本小题满分 １２ 分) 记 max(m,n)表示 m,n中的最大值,如 max{３,１０}＝ １０．已知函数f(x)＝max{x２－１,２lnx},g(x)＝max {x＋lnx,ax２＋x}． (１)求函数f(x)在 １ ２,２[ ] 上的值域; (２)试探讨是否存在实数a,使得g(x)＜３ ２ x＋４a 对x∈(１,＋∞)恒成立? 若存在,求a 的取值范围;若不存 在,说明理由． ２２．(本小题满分 １０ 分)选修 ４－４:坐标系与参数方程: 在平面直角坐标系xOy 中,以原点O 为极点,x 轴正半轴为极轴,长度单位相同,再建立极坐标系,直线l的参 数方程为 x＝tcosα y＝y０ ＋tsinα{ (t为参数,α为l 的倾斜角),曲线 E 的极坐标方程为ρ＝４sinθ,射线θ＝β,θ＝β＋π ６, θ＝β－π ６ 与曲线E 分别交于不同于极点的三点A,B,C． (１)求证:|OB|＋|OC|＝ ３|OA|; (２)当β＝π ３ 时,直线l过B,C 两点,求y０ 与α的值． ２３．(本小题满分 １０ 分)选修 ４－５:不等式选讲: 设函数f(x)＝|x＋２|＋|x－２|,x∈R．不等式f(x)≤６ 的解集为 M． (１)求 M; (２)当a,b∈M 时,证明:３|a＋b|≤|ab＋９|． ４－３