- 551.50 KB
- 2021-02-26 发布
高新部高二6月月考文科数学试题
一、选择题(每题5分,共60分)
1.东方中学共有160名教职工,其中一般教师120名,行政人员16名,后勤人员24名.为了了解教职工对学校在校务公开方面的意见,用分层抽样抽取一个容量为20的样本,则应抽取的后勤人员人数是( ).
A. 3 B. 2 C. 15 D. 4
2.复数=
A. B. C. D.
3.关于右侧茎叶图的说法,结论错误的一个是( )
A. 甲的极差是29 B. 甲的中位数是25
C. 乙的众数是21 D. 甲的平均数比乙的大
4.进入互联网时代,经常发送电子邮件,一般而言,发送电子邮件要分成以下几个步骤:(a).打开电子邮件;(b)输入发送地址;(c)输入主题;(d)输入信件内容;(e)点击“写邮件”;(f)点击“发送邮件”;正确的步骤是
A. B.
C. D.
5.若复数满足,则( )
A. B. C. D.
6.定义集合运算:☆.设集合,,则集合☆的元素之和为( )
A. B. C. D.
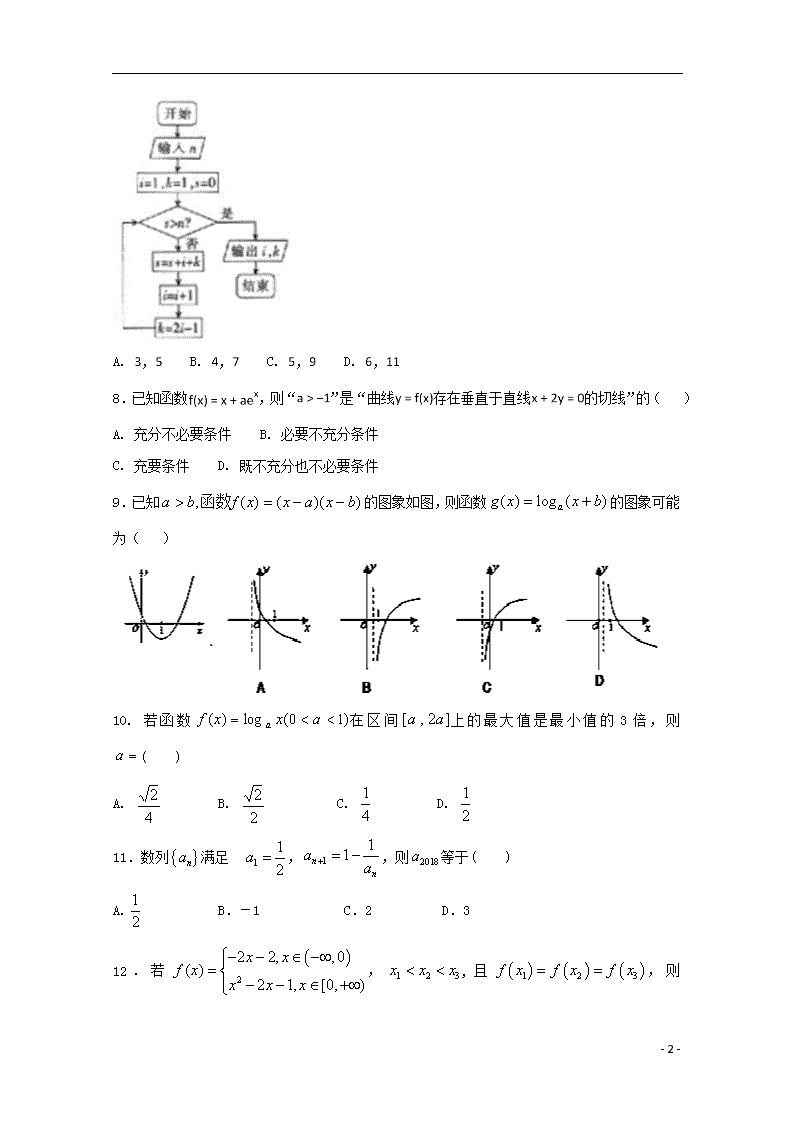
7.执行如图所示的程序框图,若输入的,则输出的,的值分别为( )
- 8 -
A. , B. , C. , D. ,
8.已知函数,则“”是“曲线存在垂直于直线的切线”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
9.已知的图象如图,则函数的图象可能为( )
10. 若函数在区间上的最大值是最小值的3倍,则( )
A. B. C. D.
11.数列满足 ,,则等于( )
A. B.-1 C.2 D.3
12.若,,且,则
- 8 -
的取值的范围是( )
A. B. C. D.
二、填空题(20分)
13.复数 的虚部为___________.
14.已知,若为实数,则_____________.
15.从中得出的一般性结论是_____________.
16.如图(1)有面积关系,则图(2)有体积关系_______________
三、解答题:共70分.(17题10分,其余12分)
17.设全集为,集合,.
(1)求;
(2)已知,若,求实数的取值范围.
18.已知命题:函数在上为增函数;命题:不等式对任意实数恒成立,若是真命题,求实数的取值范围.
19.(本题12分)已知函数
(1)当时,求不等式的解集;
(2),都有恒成立,求的取值范围
- 8 -
20.(本题12分)已知在直角坐标系中,圆锥曲线的参数方程为(为参数),定点,、分别是圆锥曲线的左、右焦点.
(1)以坐标原点为极点,轴正半轴为极轴建立极坐标系,求经过点且平行于直线的直线的极坐标方程;
(2)设(1)中直线与圆锥曲线交于,两点,求.
21.函数.
(1)当时,求在区间上的最值;
(2)讨论的单调性;
(3)当时,有恒成立,求的取值范围.
22.设为三角形的三边,求证:
- 8 -
1-4.ACBC 5-8. CCCB 9-12 CABB
13. 14.
15. 16. .
17.解:(1)集合,
对于集合,有且,即,
即,∴,
所以.
(2)因为.
①当,即时,,满足题意.
②当,即时,有或,
即或.
综上,实数的取值范围为.
18.解:命题为真时,函数在为增函数,
故对称轴,
从而命题为假时,.
若命题为真,当,即时,符合题意.
当时,有,
即.
故命题为真时:;为假时:或.
若为假命题,则命题,同时为假命题.
即,所以.
∴为真命题时:.
19. 解:(1)
- 8 -
等价于:或或
得:或或…………5分
解集为…………6分
(2) 化为
由于:
当且仅当:时取“=”
所以 …………12分
20. 解:(1)圆锥曲线的参数方程为(为参数),
所以普通方程为: ……………………2分
……………………4分
直线极坐标方程为:……6分
(2)直线的参数方程是(为参数),……………………8分
代入椭圆方程得……………………9分
……………………10分
……………………12分
21.【答案】(1)(2)当时,在递增;当时,在递增,在上递减.当时,在递减.(3)
- 8 -
【解析】试题分析:(1)在的最值只能在和区间的两个端点取到,因此,通过算出上述点并比较其函数值可得函数在的最值;(2)算出,对的取值范围分情况讨论即可;(3)根据(2)中得到的单调性化简不等式,从而求解不等式,解得的取值范围.
试题解析:(1)当时,,∴,
∵的定义域为,∴由,得.……………………2分
∴在区间上的最值只可能在取到,
而,,,……4分
(2),,
①当,即时,,∴在上单调递减;……5分
②当时,,∴在上单调递增;…………………………6分
③当时,由得,∴或(舍去)
∴在上单调递增,在上单调递减;……………………8分
综上,当时,在单调递增;
当时,在单调递增,在上单调递减.
当时,在单调递减;
(3)由(2)知,当时,,
即原不等式等价于,…………………………10分
- 8 -
即,整理得,
∴,………………13分
又∵,∴的取值范围为.……………………12分
22.【答案】见解析
【解析】
试题分析:本题用直接法不易找到证明思路,用分析法,要证该不等式成立,因为,所以,只需证该不等式两边同乘以转化成的等价不等式a(1+b)(1+c)+ b(1+a)(1+c)> c(1+a)(1+b)成立,用不等式性质整理为a+2ab+b+abc>c成立,用不等式性质及三角不等式很容易证明此不等式成立.
试题解析:要证明:
需证明: a(1+b)(1+c)+ b(1+a)(1+c)> c(1+a)(1+b) 5分
需证明:a(1+b+c+bc)+ b(1+a+c+ac)> c(1+a+b+ab) 需证明a+2ab+b+abc>c 10分
∵a,b,c是的三边 ∴a>0,b>0,c>0且a+b>c,abc>0,2ab>0
∴a+2ab+b+abc>c
∴成立。 12分
- 8 -