江苏省南京市2020届高三下学期5月模拟考试数学试题 Word版含解析 23页

www.ks5u.com 一、填空题（本大题共14小题，每小题5分，计70分.不需写出解答过程，请把答案写在答题纸的指定位置上）‎ ‎1.设集合M＝{m|﹣3＜m＜2，m∈Z}，N＝R，则M∩N＝_____．‎ ‎【答案】{﹣2，﹣1，0，1}‎ ‎【解析】‎ ‎【分析】‎ 可以求出集合M，然后进行交集的运算即可．‎ ‎【详解】∵M＝{﹣2，﹣1，0，1}，N＝R，‎ ‎∴M∩N＝{﹣2，﹣1，0，1}．‎ 故答案为：{﹣2，﹣1，0，1}．‎ ‎【点睛】本题考查了描述法、列举法的定义，交集的定义及运算，考查了计算能力，属于基础题．‎ ‎2.复数z复平面上对应点位于第_____象限．‎ ‎【答案】一 ‎【解析】‎ ‎【分析】‎ 首先进行复数的除法运算，分子和分母同乘以分母的共轭复数，分母变成一个实数，分子进行复数的乘法运算，整理成复数的标准形式，写出对应点的坐标，看出所在的象限．‎ ‎【详解】∵复数，‎ ‎∴复数对应的点的坐标是（，）‎ ‎∴复数在复平面内对应的点位于第一象限，‎ 故答案为：一 ‎【点睛】本题考查复数的实部和虚部的符号，是一个概念题，考查了复数的四则运算，属于简单题．‎ ‎3.某次测验，将20名学生平均分为两组，测验结果两组学生成绩的平均分和标准差分别为90，6；80，4．则这20名学生成绩的方差为_____．‎ ‎【答案】51‎ ‎【解析】‎ - 23 -‎ ‎【分析】‎ 由方差定义可得n个数与其平均数，方差间关系xxxnS2+n2，利用此关系可结合条件把20 个数据中的前10个数，后10个数分别找出其平方和，及平均数，进而求出20名学生成绩的方差．‎ ‎【详解】设x1，x2…xn的方差S2[（x1）2+（x2）2+…+（xn）2][xxx2（x1+x2+…+xn）+n2][x12+xxn2]‎ ‎∴xxxnS2+n2，‎ 则xxx10×36+10×902＝81360，xxx10×16+10×802＝64160，‎ ‎85．‎ ‎∴S2[xxx202][81360+64160﹣20×852]＝51，‎ 故答案：51．‎ ‎【点评】本题依托平均数，方差，标准差的定义关系，考查学生的数据处理能力和计算能力，属于中低档题．‎ ‎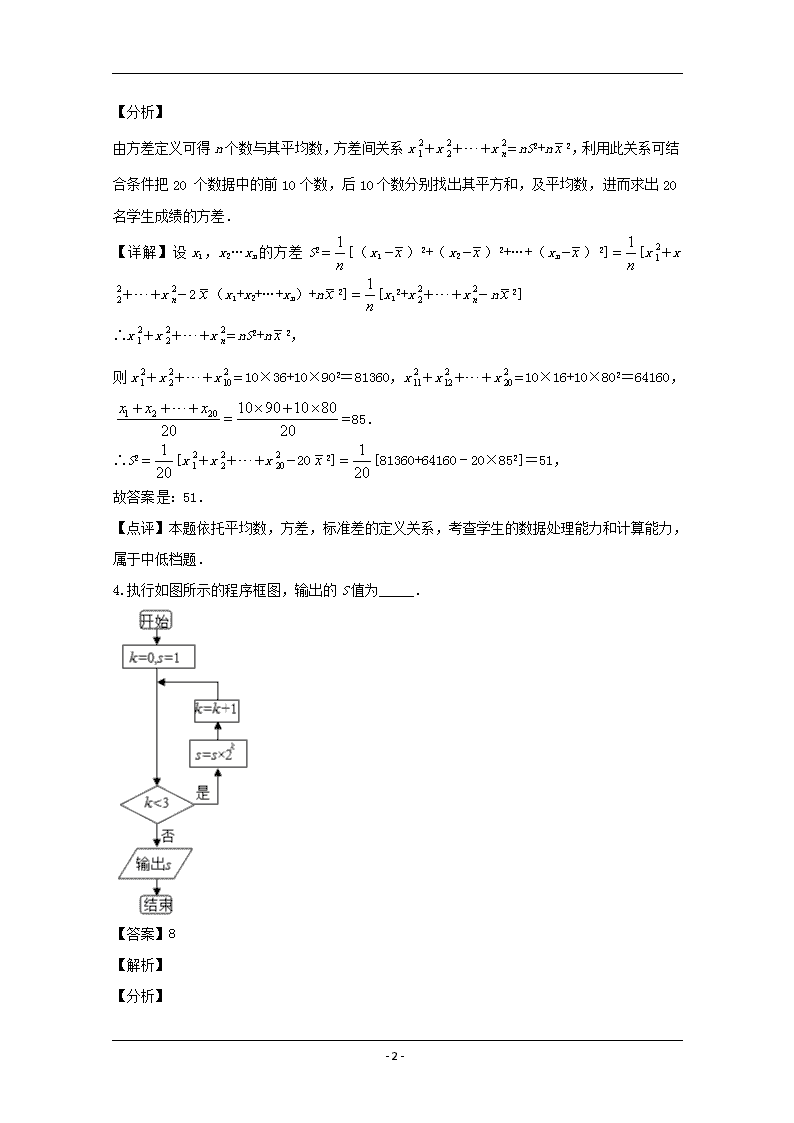4.执行如图所示的程序框图，输出的S值为_____．‎ ‎【答案】8‎ ‎【解析】‎ ‎【分析】‎ - 23 -‎ 根据程序框图进行模拟运算即可．‎ ‎【详解】第1次循环：k＝0，S＝1；‎ 第2次循环：S＝1×21＝2，k＝2；‎ 第3次循环：S＝2×22＝8，k＝3；‎ 此时不满足循环条件k＜3，输出S＝8．‎ 故答案为：8．‎ ‎【点睛】本题主要考查了程序框图的识别和判断问题，根据条件模拟运算是解题的关键，考查了计算能力，属于简单题．‎ ‎5.抛掷甲、乙两枚质地均匀且四面上分别标有1，2，3，4的正四面体，记底面上的数字分别为，则为整数的概率是_____．‎ ‎【答案】‎ ‎【解析】‎ 总数为 为整数有共8个,所以概率是 ‎ ‎6.函数f（x）=（x﹣3）ex的单调递增区间是 ．‎ ‎【答案】（2，+∞）‎ ‎【解析】‎ 试题分析：首先对f（x）=（x﹣3）ex求导，可得f′（x）=（x﹣2）ex，令f′（x）＞0，解可得答案．‎ 解：f′（x）=（x﹣3）′ex+（x﹣3）（ex）′=（x﹣2）ex，令f′（x）＞0，解得x＞2．‎ 故答案为（2，+∞）．‎ 考点：利用导数研究函数的单调性．‎ ‎7.已知双曲线的离心率为，那么此双曲线的准线方程为_____．‎ ‎【答案】‎ ‎【解析】‎ - 23 -‎ ‎【分析】‎ 利用双曲线的离心率为，求出a，c，再求出双曲线的准线方程．‎ ‎【详解】∵双曲线的离心率为，‎ ‎∴（m﹣3）（m+5）＜0，，‎ ‎∴﹣5＜m＜3，，‎ ‎∴m，‎ ‎∴a，c＝2，‎ ‎∴双曲线的准线方程为 故答案为：．‎ ‎【点睛】本题考查双曲线的准线方程，考查离心率，考查学生分析解决问题的能力，属于中档题．‎ ‎8.已知正四棱锥的体积为，底面边长为，则侧棱的长为 ．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 先设底面正方形的中心为，根据题意得到，再由求出，结合勾股定理即可得出结果.‎ ‎【详解】设底面正方形的中心为，又底面边长为2可得 由 ‎【点睛】本题主要考查棱锥的结构特征，熟记棱锥的结构特征及体积公式即可，属于基础题型.‎ - 23 -‎ ‎9.已知函数若则函数的最小正周期为 ．‎ ‎【答案】‎ ‎【解析】‎ ‎【详解】试题分析：，所以，由此可得：‎ ‎，又因为，所以令得，所以函数的最小正周期 ‎．‎ 考点：三角函数的性质．‎ ‎10.已知等差数列{an}满足：a1＝﹣8，a2＝﹣6．若将a1，a4，a5都加上同一个数m，所得的三个数依次成等比数列，则m的值为_____．‎ ‎【答案】-1‎ ‎【解析】‎ ‎【分析】‎ ‎【分析】由题意可得公差d＝a2﹣a1＝2，从而an＝a1+（n﹣1）d＝2n﹣10，设所加的这个数为x，根据 （a1+x）（a5+x），解出x的值．‎ ‎【详解】已知等差数列{an}中，a1＝﹣8，a2＝﹣6，‎ ‎∴公差d＝a2﹣a1＝2，‎ ‎∴an＝a1+（n﹣1）d＝2n﹣10．‎ 将a1，a4，a5都加上同一个数，所得的三个数依次成等比数列，设所加的这个数为x，‎ 则有 （a1+x）（a5+x），即 （﹣2+x）2＝（﹣8+x）（0+x），解得 x＝﹣1．‎ 故答案为：﹣1．‎ ‎【点睛】本题主要考查等比数列的定义和性质，求等差数列的通项公式，求得 an＝2n﹣10，是解题的关键，属于中档题．‎ ‎11.设函数和的图象在轴左、右两侧靠近 轴的交点分别为、，已知为原点，则 ．‎ - 23 -‎ ‎【答案】‎ ‎【解析】‎ 试题分析：由得，即，所以，即，则，所以 ‎；‎ 考点：1．三角函数的恒等变换；2．平面向量的数量积；‎ ‎12.设f（x）＝asin2x+bcos2x（a，b∈R），若f（x）的最大值为，则a+b的取值范围为_____．‎ ‎【答案】[，]．‎ ‎【解析】‎ ‎【分析】‎ 由条件利用辅助角公式、正弦函数的最值求得a2+b2＝5，再利用基本不等式求得 （a+b）2≤10，从而求得a+b的取值范围．‎ ‎【详解】∵f（x）＝asin2x+bcos2xsin（2x+θ）（a，b∈R），‎ 若f（x）的最大值为，∴a2+b2＝5，‎ ‎∴（a+b）2＝a2+b2+2ab≤2（ a2+b2 ）＝10，‎ ‎∴a+b，故a+b的取值范围为[，]，‎ 故答案为：[，]．‎ ‎【点睛】本题主要考查辅助角公式，正弦函数的最值，基本不等式的应用，属于中档题．‎ ‎13.在△ABC中，角A，B，C的对边分别是a，b，c，已知b＝2，且cos2B+cosB+cos（A﹣C）＝1，则a+2c的最小值为_____．‎ ‎【答案】‎ ‎【解析】‎ - 23 -‎ ‎【分析】‎ 利用二倍角公式以及两角和与差的三角函数，结合正弦定理以及基本不等式求解即可．‎ ‎【详解】解：由cos2B+cosB+cos（A﹣C）＝1‎ ‎⇒1﹣2sin2B+cosB+cosAcosC+sinAsinC＝1‎ ‎⇒1﹣2sin2B﹣cosAcosC+sinAsinC+cosAcosC+sinAsinC＝1‎ ‎⇒sinAsinC＝sin2B，‎ 由正弦定理得到ac＝b2，‎ 而，当且仅当 等号成立 由b＝2，可得．‎ 故答案为：．‎ ‎【点评】本题考查两角和与差的三角函数，正弦定理基本不等式的应用，考查分析问题解决问题的能力．‎ ‎14.已知正实数x，y满足x＋＋3y＋＝10，则xy的取值范围为________．‎ ‎【答案】‎ ‎【解析】‎ ‎10＝＋≥2，即25≥3xy＋＋143(xy)2－11xy＋8≤01≤xy≤.‎ 二、解答题（本大题共6小题，计90分.解答应写出必要的文字说明，证明过程或演算步骤，请把答案写在答题纸的指定区域内）‎ ‎15.已知△ABC的内角A，B，C的对边分别为a，b，c，向量 ‎（1）当时，求b的值；‎ ‎（2）当∥时，且，求的值．‎ ‎【答案】（1）b＝1．（2）2‎ ‎【解析】‎ ‎【分析】‎ - 23 -‎ ‎（1）由题意得，即，由正弦定理有：，联立即可得解b的值．‎ ‎（2）由平行条件得a＝sinA•sinB，由，则可得，联立即可得解．‎ ‎【详解】（1）由题意得：，‎ 即得，‎ 在三角形中由正弦定理有：，‎ 由以上两式可知：b＝1．‎ ‎（2）由平行条件得，‎ ‎， ‎ 则可得到：，‎ ‎∴．‎ ‎【点睛】本题主要考查了正弦定理，平面向量数量积的坐标运算，两角和的余弦函数公式的综合应用，考查了计算计算能力和转化思想，属于中档题．‎ ‎16.如图，四棱锥A﹣BCDE中，AB、BC、BE两两垂直且AB＝BC＝BE，DE∥BC，DE＝2BC，F是AE的中点．‎ ‎（1）求证：BF∥面ACD；‎ ‎（2）求证：面ADE⊥面ACD．‎ ‎【答案】（1）见解析（2）见解析 ‎【解析】‎ ‎【分析】‎ ‎（1）取AD的中点M，连接CM、MF，推导出四边形BCMF为平行四边形，从而CM∥BF - 23 -‎ ‎，由此能证明BF∥面ACD．‎ ‎（2）作DE中点N，连接CN，推导出CM⊥AD，BF⊥AE，CM⊥AE，由此能证明面ADE⊥面ACD．‎ ‎【详解】证明：（1）取AD的中点M，连接CM、MF．‎ ‎∵F、M分别为AE、AD中点，∴DE∥2MF，DE=2MF 又∵DE∥2BC，DE=2BC∴FM∥BC，FM=BC，‎ ‎∴四边形BCMF为平行四边形，∴CM∥BF，‎ 又∵BF⊄面ACD，CM⊂面ACD，‎ ‎∴BF∥面ACD．‎ ‎（2）作DE中点N，连接CN，‎ ‎∵DE∥2BC，DE=2BC，N为DE中点N，∴DN＝BC，‎ 又∵AB、BC、BE两两垂直，且AB＝BC＝BE，∴AC＝CD，‎ ‎∵M为AD中点，∴CM⊥AD，‎ 又∵F是AE的中点，且AB＝BE，∴BF⊥AE，‎ ‎∵CM∥BF，∴CM⊥AE，‎ 又∵AD∩AE＝A，AE、AD⊂面ADE，∴CM⊥面ADE，‎ ‎∵CM⊂面ACD，∴面ADE⊥面ACD．‎ ‎【点睛】本题考查线面平行、面面垂直的证明，考查了空间思维能力和推理能力，属于中档题．‎ ‎17.为解决城市的拥堵问题，某城市准备对现有的一条穿城公路MON进行分流，已知穿城公路MON自西向东到达城市中心点O后转向东北方向（即）．现准备修建一条城市高架道路L，L在MO上设一出入口A，在ON上设一出入口B．假设高架道路L在AB部分为直线段，且要求市中心O与AB的距离为10km．‎ - 23 -‎ ‎（1）求两站点A，B之间距离的最小值；‎ ‎（2）公路MO段上距离市中心O30km处有一古建筑群C，为保护古建筑群，设立一个以C为圆心，5km为半径的圆形保护区．则如何在古建筑群C和市中心O之间设计出入口A，才能使高架道路L及其延伸段不经过保护区（不包括临界状态）？‎ ‎【答案】（1）；（2）设计出入口A离市中心O的距离在到20km之间时，才能使高架道路L及其延伸段不经过保护区（不包括临界状态）．‎ ‎【解析】‎ ‎【分析】‎ ‎（1）过点O作于点E，则，设，则，，则有，然后利用三角函数的知识求出分母的最大值即可 ‎（2）以O为原点建立平面直角坐标系，设直线AB的方程为，可得和，解得或（舍），可得，又当时，，从而可得.‎ ‎【详解】（1）过点O作于点E，则，‎ 设，则，‎ 所以，‎ 所以；‎ - 23 -‎ 因为；‎ 所以当时，AB取得最小值为；‎ ‎（2）以O为原点建立平面直角坐标系，如图所示；‎ 则圆C的方程为，‎ 设直线AB的方程为；‎ ‎∴，∴，‎ 解得或（舍），∴，‎ 又当时，，‎ 所以；‎ 综上知，当时，即设计出入口A离市中心O的距离在到20km之间时，才能使高架道路L及其延伸段不经过保护区（不包括临界状态）．‎ ‎【点睛】1.本题考查的是三角函数的实际应用，要善于利用三角函数的有界性求最值 ‎2.由实际问题建立直角坐标系，运用直线与圆的位置关系，确定参数范围.‎ ‎18.已知点M是圆C：（x+1）2+y2＝8上的动点，定点D（1，0），点P在直线DM上，点N在直线CM上，且满足2，•0，动点N的轨迹为曲线E．‎ ‎（1）求曲线E的方程；‎ ‎（2）若AB是曲线E的长为2的动弦，O为坐标原点，求△AOB面积S的最大值．‎ ‎【答案】（1）．（2）．‎ - 23 -‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由已知得NP为DM的垂直平分线，|ND|＝|NM|，，由此能求了轨迹E的方程．‎ ‎（2）法一：设直线AB的方程为y＝kx+m，由，得（1+2k2）x2+4kmx+2m2﹣2＝0．由此利用根的判别式、韦达定理、弦长公式、点到直线的距离公式，结合已知条件能求出△AOB面积S的最大值．‎ ‎（2）法二：设直线AB的方程为y＝kx+m，由，得（1+2k2）x2+4kmx+2m2﹣2＝0．由此利用根的判别式、韦达定理、点到直线的距离公式，结合已知条件能求出△AOB面积S的最大值．‎ ‎【详解】（1）解：因为，，‎ 所以NP为DM的垂直平分线，‎ 所以|ND|＝|NM|，又因为，‎ 所以 所以动点N的轨迹是以点C（﹣1，0），D（1，0）为焦点的长轴为的椭圆．‎ 所以轨迹E的方程为． ‎ ‎（2）解法一：因为线段AB的长等于椭圆短轴的长，要使三点A、O、B能构成三角形，‎ 则弦AB不能与x轴垂直，故可设直线AB的方程为y＝kx+m，‎ 由，消去y，并整理，得（1+2k2）x2+4kmx+2m2﹣2＝0． ‎ 设A（x1，y1），B（x2，y2），又△＝16k2m2﹣4（1+2k2）（2m2﹣2）＞0，‎ 所以，‎ - 23 -‎ 因为|AB|＝2，所以，即 所以，即，‎ 因为1+k2≥1，所以． ‎ 又点O到直线AB的距离，‎ 因为h，‎ 所以S2＝h2＝2m2（1﹣m2）‎ 所以，即S的最大值为． ‎ ‎（2）解法二：因为线段AB的长等于椭圆短轴的长，要使三点A、O、B能构成三角形，‎ 则弦AB不能与x垂直，故可设直线AB的方程为y＝kx+m，‎ 由，消去y，并整理，得（1+2k2）x2+4kmx+2m2﹣2＝0．‎ 设A（x1，y1），B（x2，y2），又△＝16k2m2﹣4（1+2k2）（2m2﹣2）＞0，‎ 所以，．‎ 因为|AB|＝2，所以．‎ 因为，‎ 所以，‎ 所以，‎ 又点O到直线AB的距离，所以h．‎ 所以S2＝h2．‎ - 23 -‎ 设，则， ‎ 所以，即S的最大值为．‎ ‎【点睛】本题考查椭圆方程的求法，考查了三角形面积的最大值的求法，解题时要注意根的判别式、韦达定理、弦长公式、点到直线的距离公式的合理运用，要求较高的计算能力，本题属于难题．‎ ‎19.设首项为a1的正项数列{an}的前n项和为Sn，q为非零常数，已知对任意正整数n，m，Sn+m＝Sm+qmSn总成立．‎ ‎（1）求证：数列{an}是等比数列；‎ ‎（2）若不等的正整数m，k，h成等差数列，试比较amm•ahh与ak2k的大小；‎ ‎（3）若不等的正整数m，k，h成等比数列，试比较与的大小．‎ ‎【答案】（1）见解析（2）见解析（3）见解析 ‎【解析】‎ ‎【分析】‎ ‎（1）令n＝m＝1，得a2＝qa1，令m＝1，得Sn+1＝S1+qSn（1），从而Sn+2＝S1+qSn+1两式相减即可得出an+2＝qan+1，进而可判断出数列{an}是等比数列 ‎（2）根据m，k，h成等差数列，可知m+h＝2k，进而可判定，进而根据等比数列的通项公式分q大于、等于和小于1三种情况判断．‎ ‎（3）正整数m，k，h成等比数列，则m•h＝k2，判断出，进而根据等差根据等比数列的通项公式分a1和q大于、等于和小于1三种情况判断．‎ ‎【详解】（1）证：因为对任意正整数n，m，Sn+m＝Sm+qmSn总成立，‎ 令n＝m＝1，得S2＝S1+qS1，则a2＝qa1‎ 令m＝1，得Sn+1＝S1+qSn（1），从而Sn+2＝S1+qSn+1（2），‎ ‎（2）﹣（1）得an+2＝qan+1，（n≥1）‎ 综上得an+1＝qan（n≥1），所以数列{an}是等比数列 ‎（2）正整数m，k，h成等差数列，‎ 则m+h＝2k，‎ - 23 -‎ 所以，‎ 则 ‎①当q＝1时，amm•ahh＝a12k＝ak2k ‎②当q＞1时，‎ ‎③当0＜q＜1时，‎ ‎（3）正整数m，k，h成等比数列，则m•h＝k2，则，‎ 所以，‎ ‎①当a1＝q，即时，‎ ‎②当a1＞q，即时，‎ ‎③当a1＜q，即时，‎ ‎【点睛】本题主要考查了等比关系的确定和等比数列的性质，考查了等比数列与不等式综合，考查了分类讨论思想和计算能力，属于难题．‎ ‎20.‎ 已知函数（是自然对数的底数）.‎ ‎（1）若曲线在处的切线也是抛物线的切线，求的值；‎ ‎（2）若对于任意恒成立，试确定实数的取值范围；‎ ‎（3）当时，是否存在，使曲线在点处的切线斜率与在上的最小值相等？若存在，求符合条件的的个数；若不存在，请说明理由.‎ ‎【答案】（1）或；（2）（3）相等，一个.‎ ‎【解析】‎ ‎【分析】‎ - 23 -‎ ‎（1）求出在的切线，与联立，根据切线与抛物线只有一个交点，则；（2）分，，根据导数讨论；（3）转化为函数的零点通过导数求解.‎ ‎【详解】（1），‎ 所以在处的切线为 即： ‎ 与联立，消去得，‎ 由知，或 ‎（2）‎ ‎①当时，在上单调递增，且当时，，‎ ‎，故不恒成立，所以不合题意 ； ‎ ‎②当时，对恒成立，所以符合题意；‎ ‎③当时令，得， ‎ 当时，，‎ 当时，，‎ 故在上是单调递减，在上是单调递增, ‎ 所以 又，，‎ 综上： ‎ ‎(3)当时，‎ 由（2）知，‎ 设，‎ 则，‎ - 23 -‎ 假设存在实数，使曲线在点处的切线斜率与在上的最小值相等，即为方程的解， ‎ 令得：，‎ 因为， 所以.‎ 令，则，‎ 当是，当时，‎ 所以在上单调递减，在上单调递增，‎ ‎,故方程有唯一解为1，‎ 所以存在符合条件的，且仅有一个.‎ ‎【点睛】本题考查导数的综合应用. 复杂方程的根问题：1、转化为函数的交点求解；2、转化为函数的零点求解.‎ ‎[选做题]（本题包括A、B、C三小题，请选定其中两小题，并在答题相应的区域内作答．若多做，则按作答的前两小题评分．解答应写出文字说明、证明过程或演算步骤）‎ ‎[选修4-2：矩阵与变换]‎ ‎21.设矩阵A，求矩阵A的逆矩阵的特征值及对应的特征向量．‎ ‎【答案】λ1＝﹣1，对应一个特征向量为，λ2，对应的一个特征向量为．‎ ‎【解析】‎ ‎【分析】‎ 由矩阵A，求得丨A丨及A*，A﹣1A*，求得A﹣1，由特征多项式f（λ）＝0，求得矩阵的特征值，代入求得特征向量．‎ ‎【详解】丨A丨1﹣4＝﹣3，A*，‎ - 23 -‎ A的逆矩阵为A﹣1A*，‎ 则特征多项式为f（λ）＝（λ）2λ2λ，‎ 令f（λ）＝0，解得：λ1＝﹣1，λ2，‎ 设特征向量为，则，‎ 可知特征值λ1＝﹣1，对应的一个特征向量为，‎ 同理可得特征值λ2，对应一个特征向量为．‎ ‎【点睛】本题考查求矩阵特征值及特征向量，考查逆矩阵的求法，考查计算能力，属于中档题．‎ ‎[选修4-4：坐标系与参数方程]‎ ‎22.在极坐标系中，求曲线关于直线对称的曲线的极坐标方程.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 将曲线和直线的极坐标方程转化成直角坐标方程，从而求得对称曲线的直角坐标方程，再转化成极坐标方程.‎ ‎【详解】以极点为坐标原点，极轴为x轴建立直角坐标系，‎ 则曲线的直角坐标方程为，且圆心C为.‎ 直线的直角坐标方程为，‎ 因为圆心C关于的对称点为，‎ 所以圆心C关于的对称曲线为.‎ - 23 -‎ 所以曲线关于直线对称的曲线的极坐标方程为.‎ ‎【点睛】本题考查极坐标方程与普通方程的互化问题，考查函数与方程思想、转化与化归思想，考查逻辑推理能力、运算求解能力.‎ ‎[选修4-5：不等式选讲] ‎ ‎23.若关于x的不等式x2﹣ax+b＜0的解集为（1，2），求函数f（x）＝（a﹣1）（b﹣1）的最大值．‎ ‎【答案】．‎ ‎【解析】‎ 分析】‎ 由题意可得1，2是方程x2﹣ax+b＝0的两根，运用韦达定理可得a＝3，b＝2，即有f（x）＝2，运用柯西不等式即可得到所求最大值．‎ ‎【详解】关于x的不等式x2﹣ax+b＜0的解集为（1，2），‎ 可得1，2是方程x2﹣ax+b＝0的两根，‎ 即有1+2＝a，1×2＝b，‎ 解得a＝3，b＝2，‎ 则函数f（x）＝（a﹣1）（b﹣1）2，‎ 由x﹣3≥0，4﹣x≥0可得3≤x≤4，‎ 由柯西不等式可得，（2）2≤（4+1）（x﹣3+4﹣x），‎ 即有2．‎ 当2，即为x∈[3，4]时，‎ f（x）取得最大值．‎ ‎【点睛】本题考查函数的最值的求法，注意运用柯西不等式，考查二次方程和二次不等式的转化思想，考查运算能力，属于中档题．‎ ‎[必做题]（第22、23题，每小题10分，计20分．请把答案写在答题纸的指定区域内）‎ - 23 -‎ ‎24.某高校设计了一个实验学科的实验考查方案：考生从6道备选题中一次性随机抽取3题，按照题目要求独立完成全部实验操作．规定：至少正确完成其中2题的便可提交通过．已知6道备选题中考生甲有4道题能正确完成，2道题不能完成．‎ ‎（1）求出甲考生正确完成题数的概率分布列，并计算数学期望；‎ ‎（2）若考生乙每题正确完成的概率都是，且每题正确完成与否互不影响．试从至少正确完成2题的概率分析比较两位考生的实验操作能力．‎ ‎【答案】（1）见解析，2．（2）此甲的实验操作能力较强．‎ ‎【解析】‎ ‎【分析】‎ ‎（1）设考生甲正确完成实验操作的题数分别为X，则 ，k＝1，2，3，由此求得考生甲正确完成实验操作的题数的概率分布列．‎ ‎（2）设考生乙正确完成实验操作的题数为Y，则，求得P（Y≥2）的值、P（X≥2）的值，再根据P（X≥2）＞P（Y≥2），得出结论．‎ ‎【详解】（1）设考生甲正确完成实验操作的题数分别为X，‎ 则 ，k＝1，2，3．‎ 所以考生甲正确完成实验操作的题数的概率分布列为：‎ X ‎1‎ ‎2‎ ‎3‎ P ‎ ‎ ‎ ‎ ‎ ‎ ‎∴EX＝1232．‎ ‎（2）设考生乙正确完成实验操作的题数为Y，则，所以，k＝0，1，2，3，‎ ‎；‎ 又，且P（X≥2）＞P（Y≥2），‎ - 23 -‎ 从至少正确完成2题的概率考察，甲通过的可能性大，因此甲的实验操作能力较强．‎ ‎【点睛】本题主要考查求离散型随机变量的分布列和数学期望的方法和步骤，属于中档题．‎ ‎25.已知（其中）‎ ‎（1）求及；‎ ‎（2）试比较与的大小，并说明理由．‎ ‎【答案】（1），（2）见解析 ‎【解析】‎ ‎【详解】（Ⅰ）令，则，令，‎ 则，∴；‎ ‎（Ⅱ）要比较与的大小，即比较：与的大小， ‎ 当时，；当时，；‎ 当时，；‎ 猜想：当时，，下面用数学归纳法证明：‎ 由上述过程可知，时结论成立，‎ 假设当时结论成立，即，‎ 两边同乘以3 得：‎ 而 ‎∴‎ 即时结论也成立，‎ ‎∴当时，成立.‎ 综上得，当时，；‎ 当时，；当时， ‎ - 23 -‎ 考点：数学归纳法 - 23 -‎ - 23 -‎