与12167726不重复 2020-2021学年辽宁省抚顺市抚顺县九年级（上）期中数学试卷 解析版 23页

2020-2021 学年辽宁省抚顺市抚顺县九年级（上）期中数学试卷 一、选择题（每小题 3 分，共 30 分） 1．下列关于 x 的方程是一元二次方程的是（ ） A．x2+1＝0 B．x+ ＝1 C．ax2+bx+c＝0 D．2x2﹣5xy+6y2＝0 2．下列图形中，既是轴对称图形又是中心对称图形的是（ ） A． B． C． D． 3．方程 x2＝1 的解集是（ ） A．x＝1 B．x＝﹣1 C．x1＝1 x2＝0 D．x1＝﹣1 x2＝1 4．某型号的手机连续两次降价，每个售价由原来的 1185 元降到了 580 元，设平均每次降价 的百分率为 x，列出方程正确的是（ ） A．580（1+x）2＝1185 B．1185（1+x）2＝580 C．580（1﹣x）2＝1185 D．1185（1﹣x）2＝580 5．将抛物线 y＝x2 向左平移 1 个单位长度，得到抛物线的解析式是（ ） A．y＝（x+1）2 B．y＝（x﹣1）2 C．y＝x2+1 D．y＝x2﹣1 6．关于 x 的方程 x2+2x﹣m＝0 有两个相等的实数根，则 m 的值是（ ） A．m＝1 B．m＝﹣1 C．m＝2 D．m＝﹣2 7．已知抛物线 y＝x2﹣x﹣2 与 x 轴的一个交点为（m，0），则代数式 m2﹣m+2018 的值（ ） A．2017 B．2018 C．2019 D．2020 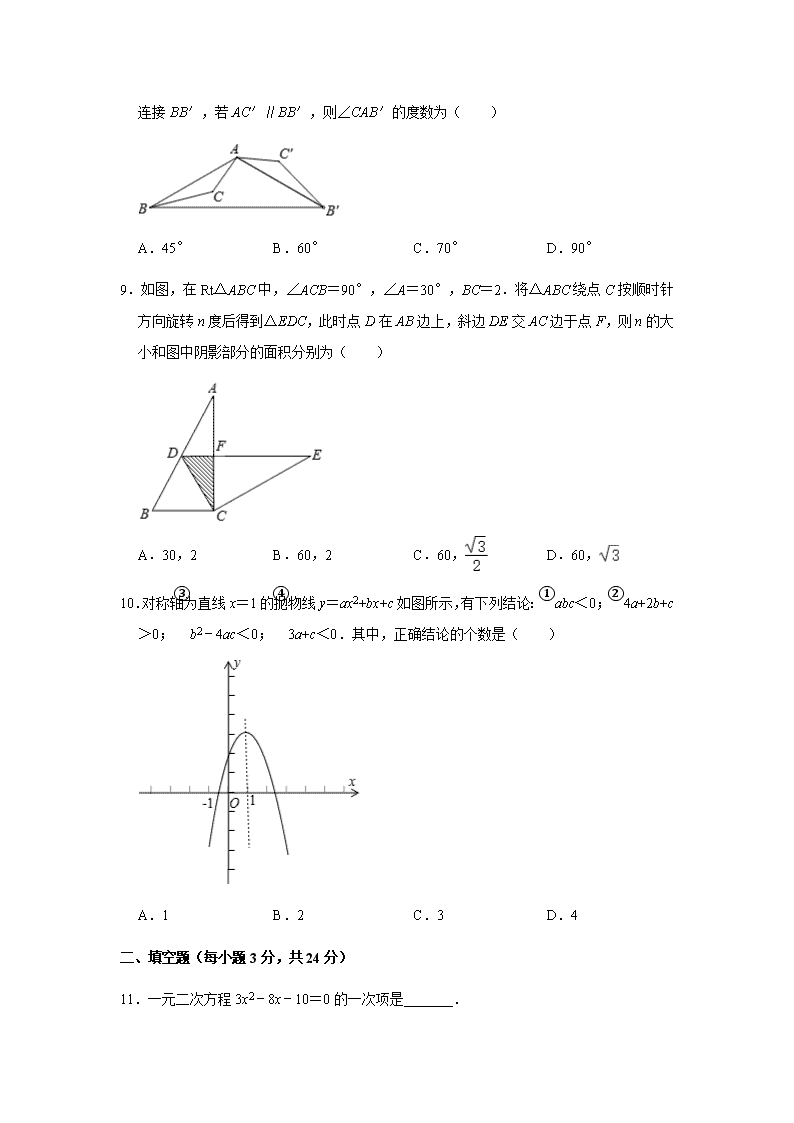8．如图，△ABC 为钝角三角形，将△ABC 绕点 A 按逆时针方向旋转 120°得到△AB′C′， 连接 BB′，若 AC′∥BB′，则∠CAB′的度数为（ ） A．45° B．60° C．70° D．90° 9．如图，在 Rt△ABC 中，∠ACB＝90°，∠A＝30°，BC＝2．将△ABC 绕点 C 按顺时针 方向旋转 n 度后得到△EDC，此时点 D 在 AB 边上，斜边 DE 交 AC 边于点 F，则 n 的大 小和图中阴影部分的面积分别为（ ） A．30，2 B．60，2 C．60， D．60， 10．对称轴为直线 x＝1 的抛物线 y＝ax2+bx+c 如图所示，有下列结论： ① abc＜0； ② 4a+2b+c ＞0； ③ b2﹣4ac＜0； ④ 3a+c＜0．其中，正确结论的个数是（ ） A．1 B．2 C．3 D．4 二、填空题（每小题 3 分，共 24 分） 11．一元二次方程 3x2﹣8x﹣10＝0 的一次项是 ． 12．抛物线 y＝﹣3（x﹣1）2﹣2 的顶点坐标是 ． 13．点 M（﹣3，2）关于原点对称的点的坐标是 ． 14．一元二次方程 x（x﹣2）+x﹣2＝0 的根是 ． 15．二次函数 y＝2x2+4x+3 的最小值是 ． 16．关于 x 的方程 x2﹣m2x+3m＝0 的两个实数根的和为 4，则 m 的值是 ． 17．已知 n 为方程 x2﹣4x+1＝0 的根，则 ＝ ． 18．将 A（2，0）绕原点顺时针旋转 30°，A 旋转后的对应点是 A1，再将 A1 绕原点顺时针 旋转 30°，A1 旋转后的对应点是 A2，再将 A2 绕原点顺时针旋转 30°，A2 旋转后的对应 点是 A3，再将 A3 绕原点顺时针旋转 30°，A3 旋转后的对应点是 A4，…按此规律继续下 去，A2020 的坐标是 ． 三、（第 19 题 10 分，第 20 题 12 分，共计 22 分） 19．（10 分）如图，方格纸中的每个小方格都是边长为 1 个单位的正方形，在建立平面直角 坐标系后，△ABC 的顶点均在格点上，点 B 的坐标为（1，0） ① 画出△ABC 关于 x 轴对称的△A1B1C1； ② 画出将△ABC 绕原点 O 按逆时针旋转 90°所得的△A2B2C2； ③ △A1B1C1 与△A2B2C2 成轴对称图形吗？若成轴对称图形，画出所有的对称轴； ④ △A1B1C1 与△A2B2C2 成中心对称图形吗？若成中心对称图形，写出所有的对称中心的 坐标． 20．（12 分）解方程： （1）3x2+6x﹣4＝0（配方法）； （2）5x2﹣4x﹣1＝0（公式法）． 四、（第 21 题 12 分，第 22 题 12 分，共计 24 分） 21．（12 分）如图，抛物线 y＝﹣x2+4x+5 与 x 轴交于 A，B 两点，与 y 轴交于点 C，抛物线 的顶点为 D． （1）求 A，B，C，D 的坐标； （2）求四边形 ABCD 的面积． 22．（12 分）为了改善小区环境，某小区决定要在一块一边靠墙（墙长 25m）的空地上修建 一个矩形绿化带 ABCD，绿化带一边靠墙，另三边用总长为 40m 的栅栏围住（如图）．若 设绿化带的 BC 边长为 xm，绿化带的面积为 ym2． （1）求 y 与 x 之间的函数解析式，并写出自变量 x 的取值范围； （2）当 x 为何值时，满足条件的绿化带的面积最大？最大为多少？ 五、解答题（12 分） 23．（12 分）如图，P 是正三角形 ABC 内的一点，且 PA＝6，PB＝8，PC＝10．若将△PAC 绕点 A 逆时针旋转后，得到△P′AB． （1）求点 P 与点 P′之间的距离； （2）求∠APB 的度数． 六、解答题（12 分） 24．（12 分）某商店销售一种销售成本为 40 元/千克的水产品，若按 50 元/千克销售，一个 月可售出 500kg，销售价每涨价 1 元，月销售量就减少 10kg． （1）写出月销售利润 y（单位：元）与售价 x（单位：元/千克）之间的函数解析式． （2）商店想在月销售成本不超过 10000 元的情况下，使月销售利润达到 8000 元，销售 单价应定为多少？ （3）当售价定位多少元时会获得最大利润？求出最大利润． 七、解答题（12 分） 25．（12 分）在 Rt△ABC 中，∠ABC＝90°，∠ACB＝30°，将 Rt△ABC 绕着点 C 顺时针 旋转一定的角度 α 得到△DEC，点 A，B 的对应点分别是 D，E． （1）当点 E 恰好在 AC 上时，如图 ① ，求∠ADE 的度数． （2）若 α ＝60°时，点 F 是边 AC 的中点，BE 与 AC 相交于点 G，如图 ② ，试判断 BF 与 DE 有怎样的数量关系和位置关系？并说明理由． 八、解答题（14 分） 26．（14 分）如图，抛物线 y＝ax2+bx+3 与 x 轴两个交点是 A（﹣1，0），B（3，0）两点， 与 y 轴交于点 C． （1）求抛物线的解析式； （2）点 M 是抛物线上的一个动点，线段 MA 绕点 M 顺时针旋转 90°得 MD，当点 D 在 y 轴上时，求点 M 的坐标； （3）P 在对称轴上，Q 在抛物线上，以 P，Q，B，C 为顶点的四边形为平行四边形，直 接写出点 P 的坐标． 2020-2021 学年辽宁省抚顺市抚顺县九年级（上）期中数学试卷 参考答案与试题解析 一、选择题（每小题 3 分，共 30 分） 1．下列关于 x 的方程是一元二次方程的是（ ） A．x2+1＝0 B．x+ ＝1 C．ax2+bx+c＝0 D．2x2﹣5xy+6y2＝0 【分析】一元二次方程必须满足两个条件： （1）未知数的最高次数是 2； （2）二次项系数不为 0． 【解答】解：A、该方程符合一元二次方程的定义，故本选项符合题意． B、该方程不是整式方程，故本选项符合题意． C、当 a＝0 时，该方程不是一元二次方程，故本选项符合题意． D、该方程中含有两个未知数，不是一元二次方程，故本选项符合题意． 故选：A． 2．下列图形中，既是轴对称图形又是中心对称图形的是（ ） A． B． C． D． 【分析】根据轴对称图形与中心对称图形的概念求解． 【解答】解：A、是轴对称图形，不是中心对称图形，故此选项不合题意； B、是轴对称图形，不是中心对称图形，故此选项不合题意误； C、既是轴对称图形又是中心对称图形，故此选项符合题意； D、是轴对称图形，不是中心对称图形，故此选项不合题意． 故选：C． 3．方程 x2＝1 的解集是（ ） A．x＝1 B．x＝﹣1 C．x1＝1 x2＝0 D．x1＝﹣1 x2＝1 【分析】利用直接开平方法求解即可． 【解答】解：x2＝1， x1＝﹣1，x2＝1． 故选：D． 4．某型号的手机连续两次降价，每个售价由原来的 1185 元降到了 580 元，设平均每次降价 的百分率为 x，列出方程正确的是（ ） A．580（1+x）2＝1185 B．1185（1+x）2＝580 C．580（1﹣x）2＝1185 D．1185（1﹣x）2＝580 【分析】根据降价后的价格＝原价（1﹣降低的百分率），本题可先用 x 表示第一次降价 后商品的售价，再根据题意表示第二次降价后的售价，即可列出方程． 【解答】解：设平均每次降价的百分率为 x， 由题意得出方程为：1185（1﹣x）2＝580． 故选：D． 5．将抛物线 y＝x2 向左平移 1 个单位长度，得到抛物线的解析式是（ ） A．y＝（x+1）2 B．y＝（x﹣1）2 C．y＝x2+1 D．y＝x2﹣1 【分析】直接根据“上加下减，左加右减”的原则进行解答． 【解答】解：将抛物线 y＝x2 向左平移 1 个单位长度，得到抛物线的解析式是 y＝（x+1） 2， 故选：A． 6．关于 x 的方程 x2+2x﹣m＝0 有两个相等的实数根，则 m 的值是（ ） A．m＝1 B．m＝﹣1 C．m＝2 D．m＝﹣2 【分析】根据根的判别式即可求出答案． 【解答】解：由题意可知：△＝4+4m＝0， ∴m＝﹣1， 故选：B． 7．已知抛物线 y＝x2﹣x﹣2 与 x 轴的一个交点为（m，0），则代数式 m2﹣m+2018 的值（ ） A．2017 B．2018 C．2019 D．2020 【分析】先求出 m2﹣m 的值，再代入代数式进行计算即可． 【解答】解：∵抛物线 y＝x2﹣x﹣2 与 x 轴的一个交点为（m，0）， ∴m2﹣m﹣2＝0， ∴m2﹣m＝2， ∴m2﹣m+2018＝2+2018＝2020． 故选：D． 8．如图，△ABC 为钝角三角形，将△ABC 绕点 A 按逆时针方向旋转 120°得到△AB′C′， 连接 BB′，若 AC′∥BB′，则∠CAB′的度数为（ ） A．45° B．60° C．70° D．90° 【分析】先根据旋转的性质得到∠BAB′＝∠CAC′＝120°，AB＝AB′，根据等腰三角 形的性质易得∠AB′B＝30°，再根据平行线的性质由 AC′∥BB′得∠C′AB′＝∠ AB′B＝30°，然后利用∠CAB′＝∠CAC′﹣∠C′AB′进行计算． 【解答】解：∵将△ABC 绕点 A 按逆时针方向旋转 120°得到△AB′C′， ∴∠BAB′＝∠CAC′＝120°，AB＝AB′， ∴∠AB′B＝ （180°﹣120°）＝30°， ∵AC′∥BB′， ∴∠C′AB′＝∠AB′B＝30°， ∴∠CAB′＝∠CAC′﹣∠C′AB′＝120°﹣30°＝90°． 故选：D． 9．如图，在 Rt△ABC 中，∠ACB＝90°，∠A＝30°，BC＝2．将△ABC 绕点 C 按顺时针 方向旋转 n 度后得到△EDC，此时点 D 在 AB 边上，斜边 DE 交 AC 边于点 F，则 n 的大 小和图中阴影部分的面积分别为（ ） A．30，2 B．60，2 C．60， D．60， 【分析】先根据已知条件求出 AC 的长及∠B 的度数，再根据图形旋转的性质及等边三角 形的判定定理判断出△BCD 的形状，进而得出∠DCF 的度数，由直角三角形的性质可判 断出 DF 是△ABC 的中位线，由三角形的面积公式即可得出结论． 【解答】解：∵△ABC 是直角三角形，∠ACB＝90°，∠A＝30°，BC＝2， ∴∠B＝60°，AC＝BC×cot∠A＝2× ＝2 ，AB＝2BC＝4， ∵△EDC 是△ABC 旋转而成， ∴BC＝CD＝BD＝ AB＝2， ∵∠B＝60°， ∴△BCD 是等边三角形， ∴∠BCD＝60°， ∴∠DCF＝30°，∠DFC＝90°，即 DE⊥AC， ∴DE∥BC， ∵BD＝ AB＝2， ∴DF 是△ABC 的中位线， ∴DF＝ BC＝ ×2＝1，CF＝ AC＝ ×2 ＝ ， ∴S 阴影＝ DF×CF＝ × ＝ ． 故选：C． 10．对称轴为直线 x＝1 的抛物线 y＝ax2+bx+c 如图所示，有下列结论： ① abc＜0； ② 4a+2b+c ＞0； ③ b2﹣4ac＜0； ④ 3a+c＜0．其中，正确结论的个数是（ ） A．1 B．2 C．3 D．4 【分析】依据函数的图象和性质逐个求解即可． 【解答】解： ① 函数的对称轴在 y 轴右侧，则 ab＜0，而 c＞0，故 abc＜0，正确，符合 题意； ② 从图象看，当 x＝2 时，y＞0，即 4a+2b+c＞0，故 ② 正确，符合题意； ③ 从图象看，抛物线与 x 轴由两个交点，故 b2﹣4ac＞0，故 ③ 错误，不符合题意； ④ 抛物线的对称轴 x＝﹣ ＝1，则 b＝﹣2a． 抛物线与 y 轴交点的纵坐标是 2，即 c＝2． 如图所示，当 x＝﹣1 时，y＜0，即 a﹣b+c＜0， 即 3a+c＜0，故 ④ 正确，符合题意； 故选：C． 二、填空题（每小题 3 分，共 24 分） 11．一元二次方程 3x2﹣8x﹣10＝0 的一次项是 ﹣8x ． 【分析】根据一元二次方程的一般形式解答． 【解答】解：一元二次方程 3x2﹣8x﹣10＝0 的一次项是﹣8x． 故答案是：﹣8x． 12．抛物线 y＝﹣3（x﹣1）2﹣2 的顶点坐标是 （1，﹣2） ． 【分析】直接利用二次函数的性质解决问题． 【解答】解：抛物线 y＝﹣3（x﹣1）2﹣2 的顶点坐标为（1，﹣2）． 故答案为（1，﹣2）． 13．点 M（﹣3，2）关于原点对称的点的坐标是 （3，﹣2） ． 【分析】平面直角坐标系中任意一点 P（x，y），关于原点的对称点是（﹣x，﹣y），记忆 方法是结合平面直角坐标系的图形记忆． 【解答】解：平面直角坐标系中任意一点 P（x，y），关于原点的对称点是（﹣x，﹣y）， ∴点 M（﹣3，2）关于原点中心对称的点的坐标是（3，﹣2）． 故答案为：（3，﹣2）． 14．一元二次方程 x（x﹣2）+x﹣2＝0 的根是 x1＝2，x2＝﹣1 ． 【分析】方程左边整理后，分解因式，利用两数相乘积为 0，两因式中至少有一个为 0 转化为两个一元一次方程来求解． 【解答】解：方程整理得：x2﹣x﹣2＝0， 分解因式得：（x﹣2）（x+1）＝0， 解得：x1＝2，x2＝﹣1． 故答案为：x1＝2，x2＝﹣1． 15．二次函数 y＝2x2+4x+3 的最小值是 1 ． 【分析】先利用配方法得到 y＝2（x+1）2+1，然后根据二次函数的性质解决问题． 【解答】解：∵y＝2x2+4x+3 ＝2（x2+2x+1﹣1）+3 ＝2（x+1）2+1， ∴当 x＝﹣1 时，y 有最小值，最小值为 1． 故答案为 1． 16．关于 x 的方程 x2﹣m2x+3m＝0 的两个实数根的和为 4，则 m 的值是 ﹣2 ． 【分析】关于 x 的方程 x2﹣m2x+3m＝0 的两个实数根的和为 4，得到 m＝±2，把 m＝2 代入 x2﹣m2x+3m＝0 得，x2﹣4x+6＝0，由△＝16﹣24＜0，得到方程 x2﹣m2x+3m＝0 无 实数根，把 m＝﹣2 代入 x2﹣m2x+3m＝0 得，x2﹣4x+6＝0，方程 x2﹣m2x+3m ＝0 有 实数根，于是得到结论． 【解答】解：∵关于 x 的方程 x2﹣m2x+3m＝0 的两个实数根的和为 4， ∴m2＝4， 解得：m＝±2， 把 m＝2 代入 x2﹣m2x+3m＝0 得，x2﹣4x+6＝0， ∵△＝16﹣24＜0， ∴方程 x2﹣m2x+3m＝0 无实数根， 把 m＝﹣2 代入 x2﹣m2x+3m＝0 得，x2﹣4x+6＝0， 方程 x2﹣m2x+3m＝0 有实数根， 故答案为：﹣2． 17．已知 n 为方程 x2﹣4x+1＝0 的根，则 ＝ 505 ． 【分析】先根据一元二次方程的解的定义得到 n2﹣4n+1＝0，即 n2+1＝4n，然后利用整 体代入得方法计算． 【解答】解：∵n 是方程 x2﹣4x+1＝0 的一个根， ∴n2﹣4n+1＝0， 即 n2+1＝4n， ∴原式＝ ＝505， 故答案为：505． 18．将 A（2，0）绕原点顺时针旋转 30°，A 旋转后的对应点是 A1，再将 A1 绕原点顺时针 旋转 30°，A1 旋转后的对应点是 A2，再将 A2 绕原点顺时针旋转 30°，A2 旋转后的对应 点是 A3，再将 A3 绕原点顺时针旋转 30°，A3 旋转后的对应点是 A4，…按此规律继续下 去，A2020 的坐标是 ． 【分析】探究规律，利用规律解决问题即可． 【解答】解：由题意：12 次一个循环， ∵2020÷12＝168 余数为 4， ∴A2020 的坐标与 A4 相同， ∵A4（﹣1，﹣ ）， ∴A2019（﹣1，﹣ ）， 故答案为（﹣1，﹣ ）． 三、（第 19 题 10 分，第 20 题 12 分，共计 22 分） 19．（10 分）如图，方格纸中的每个小方格都是边长为 1 个单位的正方形，在建立平面直角 坐标系后，△ABC 的顶点均在格点上，点 B 的坐标为（1，0） ① 画出△ABC 关于 x 轴对称的△A1B1C1； ② 画出将△ABC 绕原点 O 按逆时针旋转 90°所得的△A2B2C2； ③ △A1B1C1 与△A2B2C2 成轴对称图形吗？若成轴对称图形，画出所有的对称轴； ④ △A1B1C1 与△A2B2C2 成中心对称图形吗？若成中心对称图形，写出所有的对称中心的 坐标． 【分析】（1）将三角形的各顶点，向 x 轴作垂线并延长相同长度得到三点的对应点，顺 次连接； （2）将三角形的各顶点，绕原点 O 按逆时针旋转 90°得到三点的对应点．顺次连接各 对应点得△A2B2C2； （3）从图中可发现成轴对称图形，根据轴对称图形的性质画出对称轴即连接两对应点的 线段，做它的垂直平分线； （4）成中心对称图形，画出两条对应点的连线，交点就是对称中心． 【解答】解：如下图所示： （3）成轴对称图形，根据轴对称图形的性质画出对称轴即连接两对应点的线段，作它的 垂直平分线， 或连接 A1C1，A2C2 的中点的连线为对称轴． （4）成中心对称，对称中心为线段 BB2 的中点 P，坐标是（ ， ）． 20．（12 分）解方程： （1）3x2+6x﹣4＝0（配方法）； （2）5x2﹣4x﹣1＝0（公式法）． 【分析】（1）方程利用配方法求出解即可； （2）方程利用公式法求出解即可． 【解答】解：（1）方程整理得：x2+2x＝ ， 配方得：x2+2x+1＝ ，即（x+1）2＝ ， 开方得：x+1＝± ， 解得：x1＝﹣1+ ，x2＝﹣1﹣ ； （2）∵a＝5，b＝﹣4，c＝﹣1， ∴△＝b2﹣4ac＝16+20＝36＞0， 解得：x＝ ＝ ＝ ， 解得：x1＝1，x2＝﹣ ． 四、（第 21 题 12 分，第 22 题 12 分，共计 24 分） 21．（12 分）如图，抛物线 y＝﹣x2+4x+5 与 x 轴交于 A，B 两点，与 y 轴交于点 C，抛物线 的顶点为 D． （1）求 A，B，C，D 的坐标； （2）求四边形 ABCD 的面积． 【分析】（1）当 x＝0 时，y＝5，则 C（0，5），当 y＝0 时，﹣x2+4x+5＝0，x1＝5，x2＝ ﹣1，进而求解； （2）由 S 四边形 ABCD＝S△AOD+S△COD+S△BOC，即可求解． 【解答】解：（1）当 x＝0 时，y＝5， ∴C（0，5）， 当 y＝0 时，﹣x2+4x+5＝0，x1＝5，x2＝﹣1， ∴A（5，0），B（﹣1，0）， ∵y＝﹣x2+4x+5＝﹣（x﹣2）2+9， ∴顶点 D 的坐标（2，9）； （2）连接 OD， S 四边形 ABCD＝S△AOD+S△COD+S△BOC＝ ＝30． 22．（12 分）为了改善小区环境，某小区决定要在一块一边靠墙（墙长 25m）的空地上修建 一个矩形绿化带 ABCD，绿化带一边靠墙，另三边用总长为 40m 的栅栏围住（如图）．若 设绿化带的 BC 边长为 xm，绿化带的面积为 ym2． （1）求 y 与 x 之间的函数解析式，并写出自变量 x 的取值范围； （2）当 x 为何值时，满足条件的绿化带的面积最大？最大为多少？ 【分析】（1）依题意易求得 y 与 x 的函数关系式以及 x 的取值范围． （2）把（1）的函数关系式用配方法化简求得 y 的最大值即可． 【解答】解：（1）由题意得：y＝x ＝﹣ x2+20x， 自变量 x 的取值范围是 0＜x≤25； （2）y＝﹣ x2+20x ＝﹣ （x﹣20）2+200， ∵20＜25， ∴当 x＝20 时，y 有最大值 200 平方米 即当 x＝20 时，满足条件的绿化带面积最大． 五、解答题（12 分） 23．（12 分）如图，P 是正三角形 ABC 内的一点，且 PA＝6，PB＝8，PC＝10．若将△PAC 绕点 A 逆时针旋转后，得到△P′AB． （1）求点 P 与点 P′之间的距离； （2）求∠APB 的度数． 【分析】（1）由已知△PAC 绕点 A 逆时针旋转后，得到△P′AB，可得△PAC≌△P′AB， PA＝P′A，旋转角∠P′AP＝∠BAC＝60°，所以△APP′为等边三角形，即可求得 PP′； （2）由△APP′为等边三角形，得∠APP′＝60°，在△PP′B 中，已知三边，用勾股 定理逆定理证出直角三角形，得出∠P′PB＝90°，可求∠APB 的度数． 【解答】解：（1）连接 PP′，由题意可知 BP′＝PC＝10，AP′＝AP， ∠PAC＝∠P′AB，而∠PAC+∠BAP＝60°， 所以∠PAP′＝60 度．故△APP′为等边三角形， 所以 PP′＝AP＝AP′＝6； （2）利用勾股定理的逆定理可知： PP′2+BP2＝BP′2，所以△BPP′为直角三角形，且∠BPP′＝90° 可求∠APB＝90°+60°＝150°． 六、解答题（12 分） 24．（12 分）某商店销售一种销售成本为 40 元/千克的水产品，若按 50 元/千克销售，一个 月可售出 500kg，销售价每涨价 1 元，月销售量就减少 10kg． （1）写出月销售利润 y（单位：元）与售价 x（单位：元/千克）之间的函数解析式． （2）商店想在月销售成本不超过 10000 元的情况下，使月销售利润达到 8000 元，销售 单价应定为多少？ （3）当售价定位多少元时会获得最大利润？求出最大利润． 【分析】（1）根据月销售利润＝每千克的利润×数量就可以表示出月销售利润 y（单位： 元）与售价 x（单位：元/千克）之间的函数解析式； （2）当 y＝8000 时，代入（1）的解析式求出结论即可， （3）将（1）的解析式化为顶点式就可以求出结论． 【解答】解：（1）由题意，得 y＝（x﹣40）[500﹣10（x﹣50）]， y＝﹣10x2+1400x﹣40000． 答：y 与 x 之间的函数关系式为：y＝﹣10x2+1400x﹣40000； （2）由题意，得 8000＝﹣10x2+1400x﹣40000， 解得：x1＝60，x2＝80． 当 x＝60 时，销售成本为：40（1000﹣60×10）＝16000 元＞10000 元舍去， 当 x＝80 时，销售成本为：40（1000﹣80×10）＝8000 元＜10000 元． 答：销售单价应定为 80 元； （3）∵y＝﹣10x2+1400x﹣40000． ∴y＝﹣10（x﹣70）2+9000． ∴a＝﹣10＜0，y 有最大值． ∴当 x＝70 时．y 最大＝9000 元． 七、解答题（12 分） 25．（12 分）在 Rt△ABC 中，∠ABC＝90°，∠ACB＝30°，将 Rt△ABC 绕着点 C 顺时针 旋转一定的角度 α 得到△DEC，点 A，B 的对应点分别是 D，E． （1）当点 E 恰好在 AC 上时，如图 ① ，求∠ADE 的度数． （2）若 α ＝60°时，点 F 是边 AC 的中点，BE 与 AC 相交于点 G，如图 ② ，试判断 BF 与 DE 有怎样的数量关系和位置关系？并说明理由． 【分析】（1）如图 ① ，利用旋转的性质得 CA＝CD，∠ECD＝∠BCA＝30°，∠DEC＝ ∠ABC＝90°，再根据等腰三角形的性质和三角形内角和计算出∠CAD，从而利用互余 和计算出∠ADE 的度数； （2）如图 ② ，利用直角三角形斜边上的中线性质得到 BF＝ AC，利用含 30 度的直角 三角形三边的关系得到 AB＝ AC，则 BF＝AB，再根据旋转的性质得到∠BCE＝∠ACD ＝60°，CB＝CE，DE＝AB，从而得到 DE＝BF，由“SAS”可证△CDE≌△DCF，可得 CE＝DF＝BE，可证四边形 BEDF 是平行四边形，可得结论． 【解答】解：（1）如图 ① ，∵△ABC 绕点 C 顺时针旋转 α 得到△DEC，点 E 恰好在 AC 上， ∴CA＝CD，∠ECD＝∠BCA＝30°，∠DEC＝∠ABC＝90°， ∵CA＝CD， ∴∠CAD＝∠CDA＝ （180°﹣30°）＝75°， ∴∠ADE＝90°﹣75°＝15°； （2）BF＝DE，BF∥DE， 理由如下：如图 ② ，∵点 F 是边 AC 中点， ∴AF＝CF＝BF＝ AC， ∵∠ACB＝30°， ∴AB＝ AC， ∴BF＝AB， ∵△ABC 绕点 C 顺时针旋转 60°得到△DEC， ∴∠BCE＝∠ACD＝60°＝∠A＝∠EDC，CB＝CE，DE＝AB， ∴DE＝BF＝CF，△BCE 为等边三角形， ∴BE＝CB＝EC， 在△CDE 和△DCF 中， ， ∴△CDE≌△DCF（SAS）， ∴CE＝DF， ∴DF＝BE， 又∵BF＝DE， ∴四边形 BEDF 是平行四边形， ∴BF∥DE． 八、解答题（14 分） 26．（14 分）如图，抛物线 y＝ax2+bx+3 与 x 轴两个交点是 A（﹣1，0），B（3，0）两点， 与 y 轴交于点 C． （1）求抛物线的解析式； （2）点 M 是抛物线上的一个动点，线段 MA 绕点 M 顺时针旋转 90°得 MD，当点 D 在 y 轴上时，求点 M 的坐标； （3）P 在对称轴上，Q 在抛物线上，以 P，Q，B，C 为顶点的四边形为平行四边形，直 接写出点 P 的坐标． 【分析】（1）用待定系数法即可求解； （2）证明△MAH≌△MDG（AAS），则 MH＝MG，故 M 点的坐标为（a，a），进而求解； （3）分 PC 是边和对角线两种情况，利用数形结合的方法，即可求解． 【解答】解：（1）∵抛物线 y＝ax2+bx+3 经过 A（﹣1，0），B（3，0）两点， ∴ ，解得 ， ∴抛物线的解析式是 y＝﹣x2+2x+3； （2）过点 M 作 MH⊥AB 于点 H，作 MG⊥y 轴于点 G， ∴∠MHA＝∠MGD＝90°， ∴∠GMH＝360°﹣90°﹣90°﹣90°＝∠AMD， ∴∠AMH＝∠DMG＝90°﹣∠GMA， 又 MA＝MD， ∴△MAH≌△MDG（AAS）， ∴MH＝MG， 即 M 点的横坐标和纵坐标相同，设 M 点的坐标为（a，a）， ∴a＝﹣a2+2a+3， 解得 ， ∴ ； （3）抛物线对称轴是 ， ① 如图所示，过点 Q 作 QG 垂直于抛物线的对称轴与点 G，设 BC 交函数的对称轴于点 R， ∵四边形 PQBC 为平行四边形，则 PQ＝BC，∠BRP＝∠QPB，则∠CPB＝∠PQG， ∵∠COB＝∠PGQ＝90°， △COB≌△PGQ（AAS）， ∴CO＝PG＝3，GQ＝OB＝3， ∴点 Q 的横坐标为 4，则点 Q 纵＝﹣42+2×4+3＝﹣5， 即 GE＝5，PE＝2， ∴P1（1，﹣2）； ② 如图所示，过点 Q 作 QH 垂直于函数的对称轴于点 H， 则 Q 点的横坐标为﹣2，代入抛物线解析式中可得 Q 纵＝﹣5， ∴EH＝5，PE＝8， ∴P2（1，﹣8）； ③ 如图 4 所示，点 P 是对称轴与 x 轴的交点， ∴P3（1，0）． 综上，点 P 的坐标为（1，﹣2）或（1，﹣8）或（1，0）．