- 349.50 KB
- 2021-02-26 发布
东海高级中学 2013 届高三理科数学第一学期期中试
题
一、填空题(本大题共 14 小题,每小题 5 分,共 70 分.请将答案填入答题纸填空题的相
应答题线上.)
1.若集合 ,函数 的定义域为 ,则
▲ .
2. 将函数 的图象向左平移 个单位,再向下平移 1 个单位,得到函数
的图象,则 的解析式为 ▲ .
3. 已知向量 与 的夹角为 , ,则 在 方向上的投影为 ▲ .
4. 给出下列命题,其中正确的命题是 ▲ (填序号).
①若平面 上的直线 m 与平面 上的直线 n 为异面直线,直线 l 是 与 的交线,那么 l
至多与 m,n 中的一条相交;
②若直线 m 与 n 异面,直线 n 与 l 异面,则直线 m 与 l 异面;
③一定存在平面 同时与异面直线 m,n 都平行.
5. 函数 的定义域为 , ,对任意 , >2,则 > 的
解集为_▲ .
6. 在锐角 中,若 ,则 的取值范围是 ▲ .
7. 已知向量 , 的夹角为 45°,且 , ,则 =____▲______.
8. 如图,在正方体 中,给出以下四个结论:
① ∥平面 ;② 与平面 相交;③AD⊥平
面 ;④平面 ⊥平面 .
其中正确结论的序号是 ▲ .
9. 设定义在区间 上的函数 是奇函数 ,则
的取值范围是 ▲ .
2{ | 0}M x x x= − ≤ 2( ) log (1 | |)f x x= − N M N =
)63cos(2)(
π+= xxf 4
π
)(xg )(xg
a b 3
π
2|| =a a b
α β α β
γ
)(xf R 2)1( =−f Rx ∈ )(' xf )(xf x2 4+
ABC∆ BA 2=
b
a
a b 1|| =a 10|2| =− ba || b
1 1 1 1ABCD A B C D−
1D C 1 1A ABB 1 1A D 1BCD
1D DB 1BCD 1 1A ABB
( ),b b− ( ) 1lg1 2
axf x x
+= − ( ), , 2a b R a∈ ≠ −且 ba
A B
CD
D1
A1 B1
C1
10. 已知 是锐角 的外接圆的圆心,且 ,若 ,
则 = ▲ .(用 表示)
11. 正三棱锥 中, , , 分别是棱 上的点, 为
边 的中点, ,则三角形 的面积为______▲_______.
12. 若函数 在区间 上有最大值 ,则 的值是 ▲ .
13. 设 是自然数集的一个非空子集,对于 ,如果 ,且 ,那么 是 的
一个“酷元”,给定 ,设集合 M 由集合 S 中的两个元素构成,且
集合 中的两个元素都是“酷元”,那么这样的集合 有 ▲ .
14. 某同学为研究函数 的性质,
构造了如图所示的两个边长为 的正方形 和 ,点 是边
上的一个动点,设 ,则 .则可推知函数
的零点的个数是 ▲ .
二、解答题
15.( 本 题 满 分 14 分 ) 已 知 集 合 , 集 合
,
集合 .
(1)求 ;
(2)若 ,求实数 的取值范围.
16.(本题满分 14 分)在 中,内角 对边的边长分别是 ,且满足
, .
(1) 时,若 ,求 的面积;
O ABC∆ A θ∠ = cos cos
sin sin
B CAB ACC B
+ = 2mAO
m θ
S ABC− 2BC = 3SB = D E、 SA SB、 Q
AB SQ CDE⊥ 平面 CDE
)0(22 ≠−= aaxaxy ]3,0[ 3 a
A k A∈ 2k A∉ k A∉ k A
{ }2lg(36 )S x N y x= ∈ = −
M M
( ) ( ) ( )221 1 1 0 1f x x x x= + + + − ≤ ≤
1 ABCD BEFC P
BC CP x= ( )f x AP PF= +
( ) ( )5 11g x f x= −
}145|{ 2 −−== xxyxA
)}127lg(|{ 2 −−−== xxyxB
}121|{ −≤≤+= mxmxC
A B
ACA = m
ABC△ A B C, , a b c, ,
2 2 4a b ab+ = +
3C
π=
2A
π≠ sin sin( ) 2sin 2C B A A+ − = ABC△
F
E
P
D C
BA
(2)求 的面积等于 的一个充要条件.
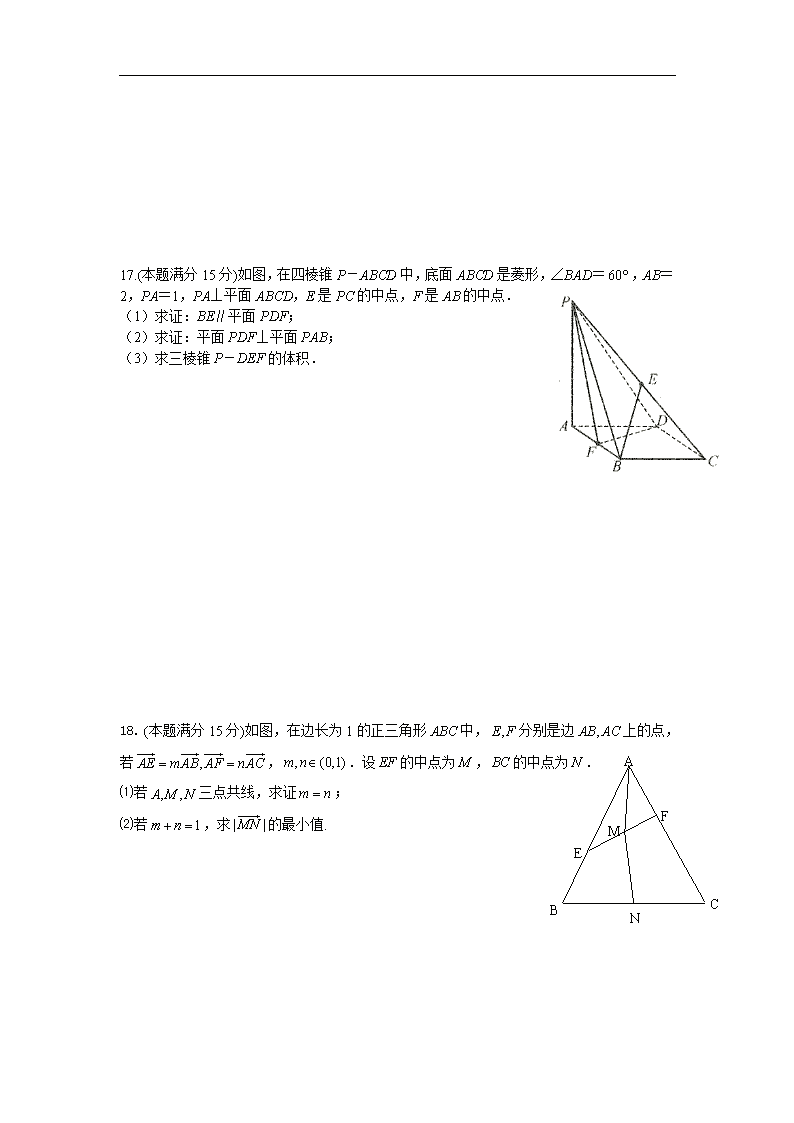
17.(本题满分 15 分)如图,在四棱锥 P-ABCD 中,底面 ABCD 是菱形,∠BAD= ,AB=
2,PA=1,PA⊥平面 ABCD,E 是 PC 的中点,F 是 AB 的中点.
(1)求证:BE∥平面 PDF;
(2)求证:平面 PDF⊥平面 PAB;
(3)求三棱锥 P-DEF 的体积.
18. (本题满分 15 分)如图,在边长为 1 的正三角形 中, 分别是边 上的点,
若 , .设 的中点为 , 的中点为 .
⑴若 三点共线,求证 ;
⑵若 ,求 的最小值.
ABC△ 3
60°
ABC ,E F ,AB AC
,AE mAB AF nAC= = , (0,1)m n∈ EF M BC N
, ,A M N m n=
1m n+ = | |MN
A
B C
E
F
M
N
19. (本题满分 16 分)已知 A、B、C 为△ABC 的三个内角,设
.
(1)当 取得最小值时,求 的大小;
(2)当 时,记 ,试求 的表达式及定义域;
(3)在(2)的条件下,是否存在向量 ,使得函数 的图象按向量 平移后得
到函数 的图象?若存在,求出向量 的坐标;若不存在,请说明理由.
20、(本题满分 16 分)已知函数 .
(1)若 时, 恒成立,求实数 的取值范围;
2 2( , ) sin 2 cos 2f A B A B= +
3 sin 2 cos 2 2A B− − +
( , )f A B C
2C π= ( ) ( , )h A f A B= ( )h A
p ( )h A p
( ) 2cos2g A A= p
ax
axaxxxf axx <
≥
×−
+−= − ,
,
244
1)(
2
ax < 1)( )2,0( at ∈
)2,0(,1)( attttg ∈−= 011)(' 2
>+=
ttg
tttg 1)( −= )2,0( a
a
aagtg 2
12)2()( −=<
a
a
a 2
122
4 −≥
a
a 22
5 ≥⇒ 5)2( 2 ≤⇒ a 52 ≤⇒ a
5log2≤⇒ a
ax ≥ 1)( 2 +−= axxxf 41)2()(
2
2 aaxxf −+−=
02
≥⇔≤ aaa )(xf ),[ +∞a
1)()( min == afxf
042
<≤−⇔> aaa )(xf )2,[ aa
),2( +∞a
41)2()(
2
min
aafxf −==
ax ≥
≥
<≤−−=
0,1
04,41)(
2
min
a
aa
xf
ax < axxxf −×−= 244)( tx =2 )2,0( at ∈
aaa tttth 4
4)2
2(2
4)( 22 −−=−=
2
12222
20 2 >⇔>⇔<< aaa
a )(th )2
2,0( a )2,2
2( a
a
aahth 4
4)2
2()( min −==
2
12222
2 2 ≤⇔≤⇔≥ aaa
a )(th )2,0( a
所以,此时, 在 上无最小值; ---------------------------------------------11 分.
所以由③④可得当 时有:当 时, ;
当 时,无最小值.----------------- -------------12 分.
所以,由①②③④可得:
当 时,因为 ,所以函数 ;---------------------------13 分.
当 时, 因为 ,函数 无最小值; --------------------------------14 分.
当 时, ,函数 无最小值.--------- ----------------15 分.
综上所述,当 时,函数 有最小值为 ;当 时,函数 无最
小值.
所以函数 在实数集 上有最小值时,实数 的取值范围为 .---------16 分.
)0,44())0(),2(()( −=∈ aa hhth
)(th )2,0( a
ax <
2
1>a athxf 4
4)()( minmin −==
2
1≤a
2
1>a 14
4 <−
a axf 4
4)( min −=
2
10 ≤≤ a 1044 <<−a )(xf
04 <≤− a 41344
2aa −≤−<− )(xf
2
1>a )(xf a4
4−
2
14 ≤≤− a )(xf
)(xf R a ),2
1( +∞