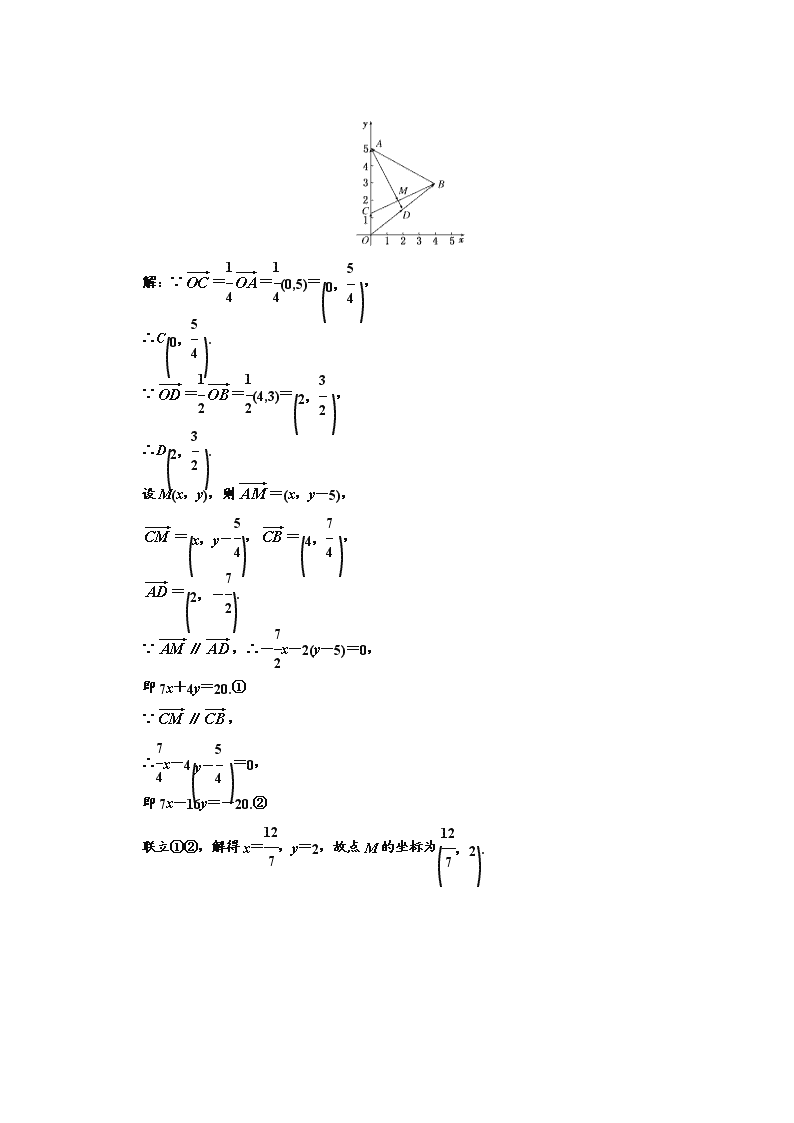- 178.50 KB
- 2021-02-26 发布
课时达标检测(二十一)平面向量共线的坐标表示
一、选择题
1.若 a=(6,6),b=(5,7),c=(2,4),则下列命题成立的是( )
A.a-c 与 b 共线 B.b+c 与 a 共线
C.a 与 b-c 共线 D.a+b 与 c 共线
答案:C
2.已知向量 a=(1,0),b=(0,1),c=ka+b(k∈R),d=a-b,如果 c∥d,那么( )
A.k=1 且 c 与 d 同向
B.k=1 且 c 与 d 反向
C.k=-1 且 c 与 d 同向
D.k=-1 且 c 与 d 反向
答案:D
3.已知向量 a=(2,3),b=(-1,2),若 ma+nb 与 a-2b 共线,则m
n
等于( )
A.-1
2 B.1
2
C.-2 D.2
答案:A
4.已知 a=(5,-2),b=(-4,-3),c=(x,y),且 2a+b-3c=0,则 c 等于( )
A.
-2,7
3 B. 2,7
3
C. 2,-7
3 D.
-2,-7
3
答案:C
5.已知 a=(-2,1-cos θ),b= 1+cos θ,-1
4 ,且 a∥b,则锐角θ等于( )
A.45° B.30°
C.60° D.30°或 60°
答案:A
二、填空题
6.已知 AB
=(6,1), BC
=(x,y),CD
=(-2,-3),若 BC
∥ DA
,则 x+2y 的值为
________.
答案:0
7.已知向量 a=(2,-1),b=(-1,m),c=(-1,2),若(a+b)∥c,则 m=________.
答案:-1
8.在△ABC 中,点 P 在 BC 上,且 BP
=2 PC
,点 Q 是 AC 的中点,若 PA
=(4,3),PQ
=(1,5),则 BC
=________.
答案:(-6,21)
三、解答题
9.平面内给定三个向量 a=(3,2),b=(-1,2),c=(4,1),回答下列问题:
(1)求 3a+b-2c;
(2)求满足 a=mb+nc 的实数 m,n;
(3)若(a+kc)∥(2b-a),求实数 k.
解:(1)3a+b-2c=3(3,2)+(-1,2)-2(4,1)
=(9,6)+(-1,2)-(8,2)
=(9-1-8,6+2-2)=(0,6).
(2)∵a=mb+nc,
∴(3,2)=m(-1,2)+n(4,1)=(-m+4n,2m+n).
∴-m+4n=3 且 2m+n=2,解得 m=5
9
,n=8
9.
(3)∵(a+kc)∥(2b-a),
又 a+kc=(3+4k,2+k),2b-a=(-5,2),
∴2×(3+4k)-(-5)×(2+k)=0.
∴k=-16
13.
10.已知 A(2,1),B(0,4),C(1,3),D(5,-3).判断 AB
与CD
是否共线?如果共线,它
们的方向相同还是相反?
解: AB
=(0,4)-(2,1)=(-2,3),
CD
=(5,-3)-(1,3)=(4,-6).
∵(-2)×(-6)-3×4=0,
∴ AB
与CD
共线且方向相反.
11.如图所示,已知△AOB 中,A(0,5),O(0,0),B(4,3), OC
=1
4 OA
, OD
=1
2 OB
,
AD 与 BC 相交于点 M,求点 M 的坐标.
解:∵OC
=1
4OA
=1
4(0,5)= 0,5
4 ,
∴C 0,5
4 .
∵OD
=1
2OB
=1
2(4,3)= 2,3
2 ,
∴D 2,3
2 .
设 M(x,y),则 AM
=(x,y-5),
CM
= x,y-5
4 ,CB
= 4,7
4 ,
AD
= 2,-7
2 .
∵ AM
∥ AD
,∴-7
2x-2(y-5)=0,
即 7x+4y=20.①
∵CM
∥CB
,
∴7
4x-4 y-5
4 =0,
即 7x-16y=-20.②
联立①②,解得 x=12
7
,y=2,故点 M 的坐标为
12
7
,2 .
相关文档
- 四年级上册数学单元测试- 第八单元2021-02-27 09:11:449页
- 2020春五年级数学下册2因数与倍数22021-02-27 09:11:4320页
- 四川省成都市成都外国语学校2019-22021-02-27 09:11:4220页
- 2014新版人教版小学六年级数学上册2021-02-27 09:11:411页
- 2020高中数学 第2章 平面解析几何2021-02-27 09:11:404页
- 数学文卷·2018届陕西省黄陵中学高2021-02-27 09:11:3811页
- 2014高考金钥匙数学解题技巧大揭秘2021-02-27 09:11:3812页
- 人教部编版一年级数学上册第八单元2021-02-27 09:11:3813页
- 眉山市2016年中考数学卷2021-02-27 09:11:384页
- 高一数学同步辅导教材(第9讲)2021-02-27 09:11:376页