2020高中数学 每日一题之快乐暑假 第19天 测量角度问题 理 新人教A版 4页

第19天 测量角度问题 高考频度：★★☆☆☆ 难易程度：★★☆☆☆‎ 典例在线 ‎（1）某观察站C与两灯塔A、B的距离分别为‎300 m和‎500 m，测得灯塔A在观察站C北偏东30°，灯塔B在观察站C正西方向，则两灯塔A、B间的距离为 A．‎500 m B．‎‎600 m C．‎700 m D．‎‎800 m ‎（2）一船以‎24 km/h的速度向正北方向航行，在点A处望见灯塔S在船的北偏东30°方向上，15 min后到点B处望见灯塔在船的北偏东65°方向上，则船在点B时与灯塔S的距离是_____________ km．(精确到 km，)‎ ‎【参考答案】（1）C；（2）． ‎ ‎ ‎ ‎（2）作出示意图如图所示．‎ ‎ ‎ 4‎ 由题意知，，由正弦定理，可得 km．‎ ‎【解题必备】（1）测量角度问题主要涉及海上、空中的追及与拦截，此时问题涉及方向角、方位角等概念，若是观察建筑物、山峰等，则会涉及俯角、仰角等概念．‎ ‎（2）解决此类问题的关键是根据题意和图形及有关概念，确定所求的角在哪个三角形中，该三角形中已知哪些量，需要求哪些量．解题时应认真审题，结合图形去选择正、余弦定理，这是最重要的一步．‎ 学霸推荐 ‎1．如图所示，从气球测得正前方的河流的两岸的俯角分别为，此时气球的高度是，则河流的宽度等于 ‎ ‎ ‎ A． B．‎ C． D．‎ ‎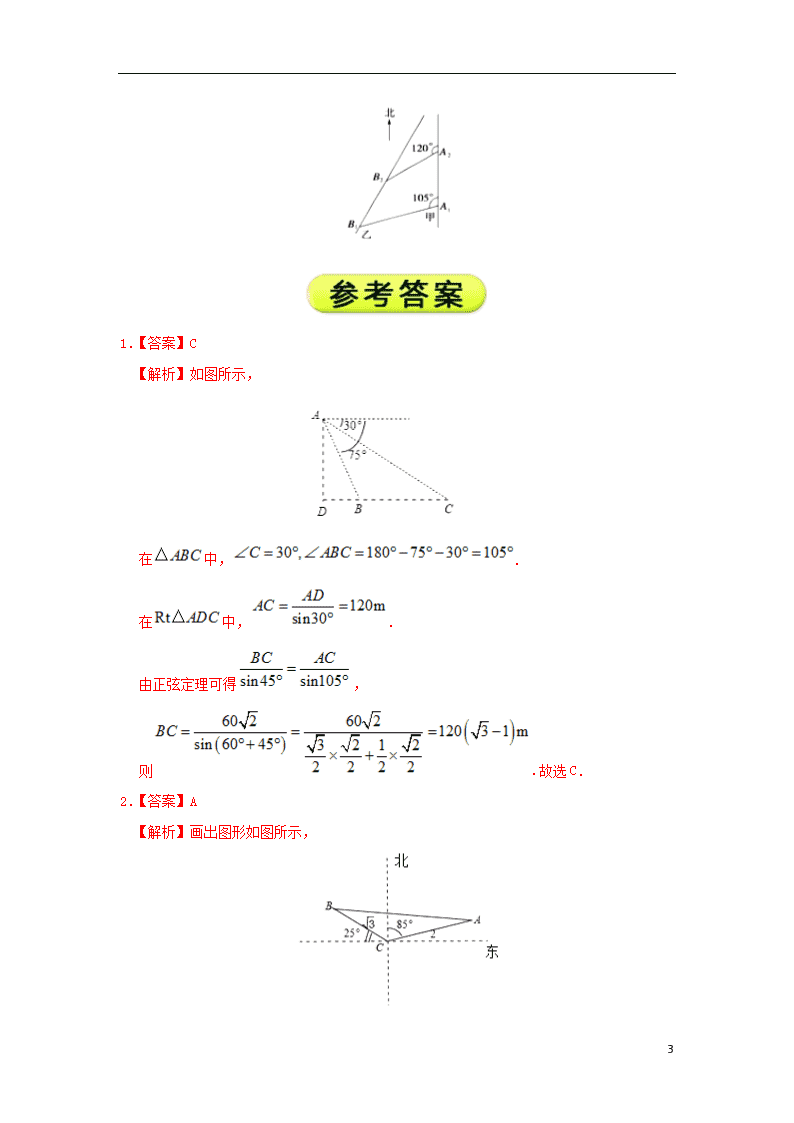2．已知船在灯塔北偏东且到的距离为，船在灯塔西偏北且到的距离为，则两船的距离为 A． B．‎ C． D．‎ ‎3．如图所示，甲船以每小时的速度向正北方向航行，乙船按固定方向匀速直线航行，当甲船位于处时，乙船位于甲船的北偏西方向的处，此时两船相距．当甲船航行到达处时，乙船航行到甲船的北偏西方向的处，此时两船相距，问乙船每小时航行多少？‎ 4‎ ‎ ‎ ‎ ‎ ‎1．【答案】C ‎【解析】如图所示，‎ ‎ ‎ 在中，.‎ 在中，.‎ 由正弦定理可得， ‎ 则.故选C．‎ ‎2．【答案】A ‎【解析】画出图形如图所示，‎ ‎ ‎ 4‎ 由题意可得，又，‎ 在中，由余弦定理可得，所以，‎ 则两船的距离为.选A. ‎ ‎ ‎ 在中，由余弦定理，得，所以.‎ 因此，乙船速度的大小为.‎ 答：乙船每小时航行.‎ ‎ ‎ 4‎