- 252.00 KB
- 2024-05-29 发布
康杰中学2017—2018学年度第一学期期中考试
高二数学(理)试题
2017.11
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若直线ax+2y+3a=0与直线3x+(a-1)y=-7+a平行,则实数a=( )
A.3 B.-2 C.-2或3 D.-3或2
2.直线ax-y+2a=0与圆x2+y2=9的位置关系是( )
A.相离 B.相切 C.相交 D.不确定
3. 如图是一几何体的直观图、正视图和俯视图.在正视图右侧,按照画三视图的要求画出的该几何体的侧视图是( )
4.已知l,m表示两条不同的直线,α表示平面,则下列说法正确的是( )
A.若l⊥α,m⊂α,则l⊥m B.若l⊥m,m⊂α,则l⊥α
C.若l∥m,m⊂α,则l∥α D.若l∥α,m⊂α,则l∥m
5. 已知圆C1:(x+1)2+(y-1)2=1,圆C2与圆C1关于直线l:x-y-1=0对称,则圆C2的方程为( )
A.(x-2)2+(y+2)2=1 B.(x+2)2+(y-2)2=1
C.(x-2)2+(y-2)2=1 D.(x-2)2+(y-1)2=1
6. 正六棱柱的底面边长为2,最长的一条对角线长为2,则它的表面积为( )
A.4(3+4) B.12(+2)
C.12(2+1) D.3(+8)
7. 过点(0,-1)的直线l与半圆C:x2+y2-4x+3=0(y≥0)有且只有一个交点,则直线l的斜率k的取值范围为( )
A. B.
C. D.
8. 直线l:ax+by=0和圆C:x2+y2+ax+by=0在同一坐标系的图形只能是( )
9. 已知四边形ABCD,ÐBAD=120º,ÐBCD=60º,AB=AD=2,则AC的最大值为( )
A. B.4 C. D.8
1
1
2
2
2
2
2
正视图
侧视图
俯视图
10. 已知直三棱柱ABCA1B1C1的6个顶点都在球O的球面上,若AB=3,AC=4,AB⊥AC,AA1=12,则球O的半径为( )
A. B.2 C. D.3
11. 已知一个几何体的三视图如图所示,则这个几何体的体积是( )
A. B. C. D.
12. 已知点P(x,y)是直线kx+y+4=0(k>0)上一动点,PA,PB是圆
C:x2+y2-2y=0的两条切线,A,B是切点,若四边形PACB的最小
面积是2,则k的值为( )
A.3 B. C.2 D.2
二、填空题(本大题共4小题,每小题5分,共20分)
13. 若圆C的半径为1,其圆心与点(1,0)关于直线y=x对称,则圆C的标准方程为________.
14.已知l1,l2是分别经过点A(1,1),B(0,-1)的两条平行直线,则当l1,l2间的距离最大时,直线l1的方程是________.
15.已知在直三棱柱ABCA1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是________.
16. 四棱锥底面是一个棱长为2的菱形,且ÐDAB=60º,各侧面和底面所成角均为60º,则此棱锥内切球体积为 .
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)
求与点P(4,3)的距离为5,且在两坐标轴的截距相等的直线方程.
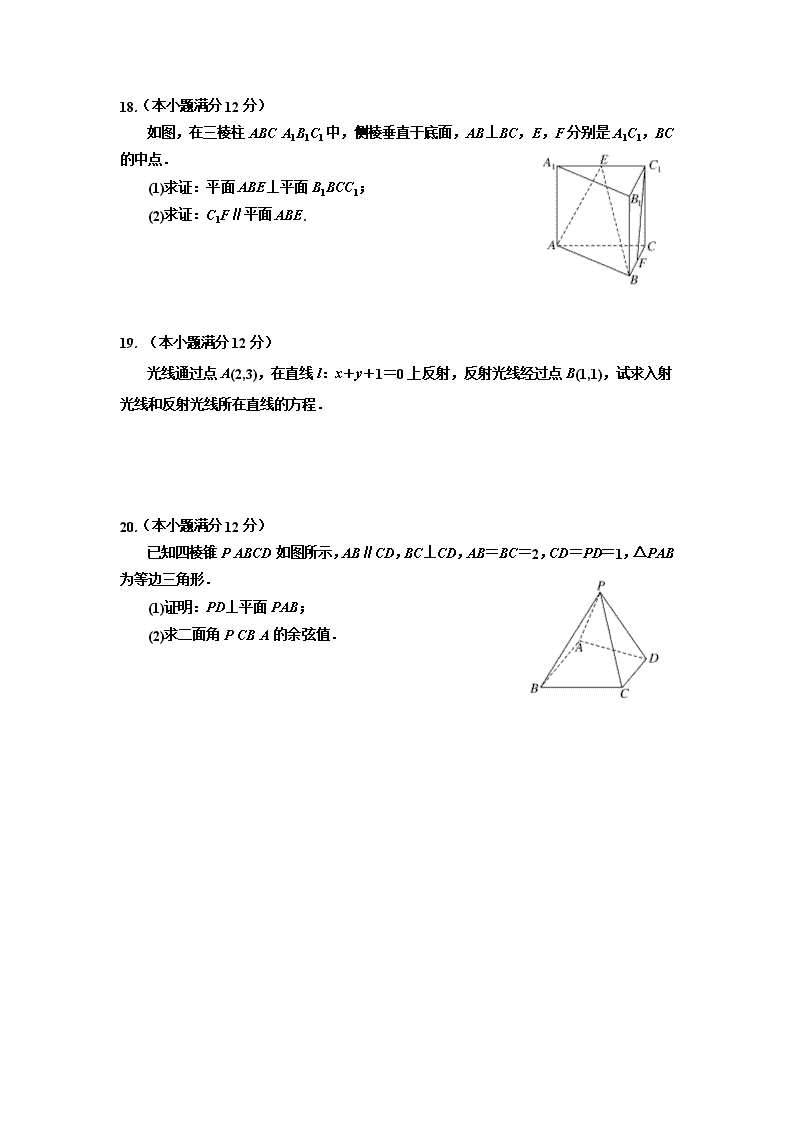
18.(本小题满分12分)
如图,在三棱柱ABCA1B1C1中,侧棱垂直于底面,AB⊥BC,E,F分别是A1C1,BC的中点.
(1)求证:平面ABE⊥平面B1BCC1;
(2)求证:C1F∥平面ABE.
19. (本小题满分12分)
光线通过点A(2,3),在直线l:x+y+1=0上反射,反射光线经过点B(1,1),试求入射光线和反射光线所在直线的方程.
20.(本小题满分12分)
已知四棱锥PABCD如图所示,AB∥CD,BC⊥CD,AB=BC=2,CD=PD=1,△PAB为等边三角形.
(1)证明:PD⊥平面PAB;
(2)求二面角PCBA的余弦值.
21.(本小题满分12分)
如图,在直角梯形ABCP中,CP∥AB,CP⊥CB,AB=BC=CP=2,D是CP中点,将△PAD沿AD折起,使得PD⊥面ABCD.
(1)求证:平面PAD⊥平面PCD;
(2)若E是PC的中点,求三棱锥APEB的体积.
22.(本小题满分12分)
已知P是直线3x+4y+8=0上的动点,PA,PB是圆C:x2+y2-2x-2y+1=0的两条切线,A,B是切点.
(1)求四边形PACB面积的最小值;
(2)直线上是否存在点P,使得∠APB=60°?若存在,求出P点的坐标;若不存在,请说明理由.
命题人:李康太
审题人:秦慧明
康杰中学2017—2018学年度第一学期期中考试
高二数学(理)试题答案
2017.11
一、 选择题:(5*12=60)
1
2
3
4
5
6
7
8
9
10
11
12
A
C
B
A
A
B
C
D
B
C
D
D
二、 填空:(5*4=20)
13. 14.
15. 16.
三、 解答题:
17:(本小题满分10分)
解:设所求直线方程为y=kx或+=1(a≠0).
对于y=kx,5=,9k2+24k+16=0,
解之得k=-.
对于x+y=a,5=,
解之得a=7+5或7-5.
故所求直线方程为y=-x或x+y-7-5=0或x+y-7+5=0.
18:(本小题满分12分)
证明:(1)由题设知,B1B⊥AB,
又AB⊥BC,B1B∩BC=B,所以AB⊥平面B1BCC1.
因为AB⊂平面ABE,
所以平面ABE⊥平面B1BCC1.
(2)取AB中点G,连接EG,FG.
因为E,F分别是A1C1,BC的中点,
所以FG∥AC,且FG=AC.
因为AC∥A1C1,且AC=A1C1,
所以FG∥EC1,且FG=EC1,
所以四边形FGEC1为平行四边形,
所以C1F∥EG.
又因为EG⊂平面ABE,所以C1F∥平面ABE.
19:(本小题满分12分)
解:设点A(2,3)关于直线l的对称点为A′(x0,y0),则
解得A′(-4,-3).
由于反射光线所在直线经过点A′(-4,-3)和B(1,1),所以反射光线所在直线的方程为y-1=(x-1)·,即4x-5y+1=0.
解方程组得反射点P.
所以入射光线所在直线的方程为
y-3=(x-2)·,即5x-4y+2=0.
20:(本小题满分12分)
(1)证明:如图,连接BD.
易知在梯形ABCD中,AD=,而PD=1,AP=2,
所以PD2+AP2=AD2,
则PD⊥PA,
同理PD⊥PB,
又PA∩PB=P,故PD⊥平面PAB.
(2)解:如图,取AB的中点M,连接PM,DM,作PN⊥DM,垂足为N,再作NH⊥BC,垂足为H,连接PH.
由(1),得AB⊥平面DPM,则
平面ABCD⊥平面DPM,所以PN⊥平面ABCD,所以PN⊥BC,PN⊥NH.
又NH⊥BC,PN∩NH=N,所以BC⊥平面NPH,
即∠NHP是二面角PCBA的平面角.
∴在Rt△HNP中,PN=,NH=1,
则PH=,cos∠NHP==,
即二面角PCBA的余弦值为.
21:(本小题满分12分)
(1) 证明:∵PD⊥底面ABCD,
∴PD⊥AD.
又由于CP∥AB,CP⊥CB,AB=BC,
∴ABCD是正方形,
∴AD⊥CD,
又PD∩CD=D,故AD⊥平面PCD,
∵AD⊂平面PAD,
∴平面PAD⊥平面PCD.
(2)解:∵AD∥BC,又BC⊂平面PBC,AD⊄平面PBC,
∴AD∥平面PBC,
∴点A到平面PBC的距离即为点D到平面PBC的距离.
又∵PD=DC,E是PC的中点,
∴DE⊥PC.
由(1)知有AD⊥平面PCD,∴AD⊥DE.
由题意得AD∥BC,故BC⊥DE.
于是,由BC∩PC=C,可得DE⊥平面PBC.
∴DE=,PC=2,
又∵AD⊥平面PCD,
∴AD⊥CP,
∵AD∥BC,∴CP⊥BC,
∴S△PEB=S△PBC=×=,
∴VAPEB=VDPEB=×DE×S△PEB=.
22:(本小题满分12分)
解:(1)如图,连接PC,由P点在直线3x+4y+8=0上,可设P点坐标为.
因为圆C的标准方程为(x-1)2+(y-1)2=1,
所以S四边形PACB=2S△PAC=2××|AP|×|AC|=|AP|.
因为|AP|2=|PC|2-|CA|2=|PC|2-1,所以当|PC|2最小时,|AP|最小.因为|PC|2=(1-x)2
+2=2+9.所以当x=-时,
|PC|=9.所以|AP|min==2,即四边形PACB面积的最小值为2.
(2)假设直线上存在点P满足题意.
因为∠APB=60°,|AC|=1,所以|PC|=2.
设P(x,y),则
整理可得25x2+40x+96=0,
所以Δ=402-4×25×96<0.
所以这样的点P是不存在的.