- 483.39 KB
- 2024-05-28 发布
5 月调研测试卷(文科数学)第 1页 共 8 页
2
0( )P K k≥ 0.050 0.010 0.005 0.001
0k 3.841 6.635 7.879 10.828
2020 年普通高等学校招生全国统一考试
5 月调研测试卷 文科数学
文科数学测试卷共 4 页。满分 150 分。考试时间 120 分钟。
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干
净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个备选项中,只有一项是符合题目要
求的。
1. 已知集合 {2 3 5 7}A , , , , 2{ | log ( 2) 1}B x x ,则 A B
A.{2} B.{3} C.{2 3}, D.{3 5},
2. 若复数 z 满足 ( i)i 2 iz ,则| |z
A. 2 B. 2 C. 10 D.10
3. 两条平行直线3 4 12 0x y 与 8 11 0ax y 之间的距离为
A. 23
10 B. 7
2 C. 23
5 D. 7
4. 下列说法正确的是
A.“若 2a ,则 2 4a ”的否命题为“若 2a ,则 2 4a ≤ ”
B.命题 p q 与 ( )p q 至少有一个为真命题
C.“ 20 2 2 0x x x , ≥ ”的否定为“ 20 2 2 0x x x , ”
D.“这次数学考试的题目真难”是一个命题
5. 为了判断英语词汇量与阅读水平是否相互独立,某语言培训机构随机抽取了 100 位英语学习者进行调查,经
过计算 2K 的观测值为 7 ,根据这一数据分析,下列说法正确的是
附:
A.有 99%以上的把握认为英语词汇量与阅读水平无关
B.有99.5%以上的把握认为英语词汇量与阅读水平有关
C.有99.9%以上的把握认为英语词汇量与阅读水平有关
D.在犯错误的概率不超过1% 的前提下,可以认为英语词汇量与阅读水平有关
6. 斐波那契数列,指的是这样一个数列:1 1 2 3 5 8 13 21 , , , , , , , , ,在数学上,斐波那契数列{ }na 定义如
下: 1 2 1 21 ( 3 )n n na a a a a n n Z , ≥ , .随着 n 的增大,
1
n
n
a
a
越来越逼近黄金分割 5 1 0.6182
,
故此数列也称黄金分割数列,而以 1na 、 na 为长和宽的长方形称为“最美长方形”,已知某“最美长方形”
5 月调研测试卷(文科数学)第 2页 共 8 页
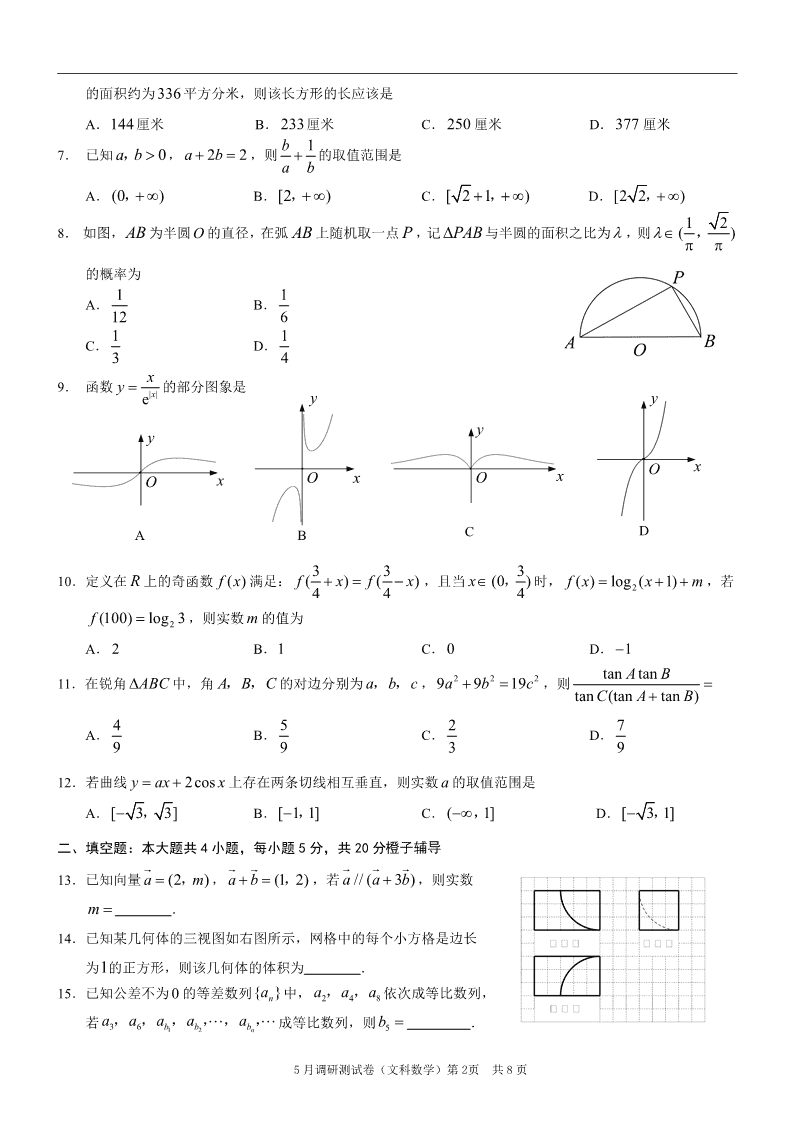
的面积约为336 平方分米,则该长方形的长应该是
A.144厘米 B. 233厘米 C. 250 厘米 D.377 厘米
7. 已知 0a b , , 2 2a b ,则 1b
a b
的取值范围是
A. (0 ) , B.[2 ) , C.[ 2 1 ) , D.[2 2 ) ,
8. 如图,AB 为半圆O 的直径,在弧 AB 上随机取一点 P ,记 PAB 与半圆的面积之比为 ,则 1 2( )
,
的概率为
A. 1
12
B. 1
6
C. 1
3 D. 1
4
9. 函数 | |e x
xy 的部分图象是
10.定义在 R 上的奇函数 ( )f x 满足: 3 3( ) ( )4 4f x f x ,且当 3(0 )4x , 时, 2( ) log ( 1)f x x m ,若
2(100) log 3f ,则实数 m 的值为
A. 2 B.1 C. 0 D. 1
11.在锐角 ABC 中,角 A B C, , 的对边分别为 a b c, , , 2 2 29 9 19a b c ,则 tan tan
tan (tan tan )
A B
C A B
A. 4
9
B. 5
9
C. 2
3
D. 7
9
12.若曲线 2cosy ax x 上存在两条切线相互垂直,则实数 a 的取值范围是
A.[ 3 3] , B.[ 1 1] , C. ( 1], D.[ 3 1] ,
13.已知向量 (2 )a m , , (1 2)a b , ,若 // ( 3 )a a b ,则实数
m .
14.已知某几何体的三视图如右图所示,网格中的每个小方格是边长
为1的正方形,则该几何体的体积为 .
15.已知公差不为 0 的等差数列{ }na 中, 2 4 8a a a, , 依次成等比数列,
若 1 23 6 nb b ba a a a a , , , , , , 成等比数列,则 5b .
O x
y
O x
y
O x
y
O x
y
A B C D
二、填空题:本大题共 4 小题,每小题 5 分,共 20 分橙子辅导
5 月调研测试卷(文科数学)第 3页 共 8 页
16.已知抛物线 2: 2 ( 0)E y px p 的焦点为 F ,以 F 为圆心、3p 为半径的圆交抛物线 E 于 P Q, 两点,以线
段 PF 为直径的圆经过点 (0 1), ,则点 F 到直线 PQ 的距离为 .
三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。第 17~21 题为必考题,每个试题考生都必
已知函数 2( ) cos( 2 ) 2 3 cos 32f x x x .
(1)求函数 ( )f x 的单调性;
(2)在 ABC 中,角 A B C, , 的对边分别为a b c, , ,且 ( ) 32
Af , 3a , 1c ,求 ABC 的面积.
18.(12 分)
今年 2 月份,我国武汉地区爆发了新冠肺炎疫情,为了预防疫情蔓延,全国各大医药厂商纷纷加紧生产口罩.
某医疗器械生产工厂为了解目前的生产力,统计了每个工人每小时生产的口罩数量(单位:箱),得到如图所示
的频率分布直方图,其中每个工人每小时的产量均落在区间[10 70], 内,数据分组为[10 20), 、[20 30), 、
[30 40), 、[40 50), 、[50 60), 、[60 70], ,已知前三组的频率成等差数列,第三组、第四组、第五组的频率
成等比数列,最后一组的频率为 1
15
.
(1)求实数 a 的值;
(2)在最后三组中采用分层抽样的方法随机抽取了 6 人,
现从这 6 人中随机抽出两人对其它小组的工人进行
生产指导,求这两人来自同一小组的概率.
19.(12 分)
如图,在三棱柱 1 1 1ABC A B C 中, 1AA 底面 ABC , 190 2ABC AB BC AA , , D E, 分别为
1BB 、 1AC 的中点.
(1)证明: DE 平面 1 1ACC A ;
(2)求点 E 到平面 ACD 的距离.
须作答。第 22、23 题为选考题,考生根据要求作答橙子辅导
。(一)必考题:共 60 分。
17.(12 分)
5 月调研测试卷(文科数学)第 4页 共 8 页
20.(12 分)
已知椭圆
2 2
2 2: 1( 0)x yC a ba b
的左、右焦点分别为 1 2F F、 ,点 2( 1 )2P , 在椭圆C 上,且 2
3 2| | 2PF .
(1)求椭圆C 的方程;
(2)过点 2F 的直线 l 与椭圆 C 交于 A B, 两点, M 为线段 AB 的中点,若椭圆 C 上存在点 N ,满足
3ON OM (O 为坐标原点),求直线l 的方程.
21.(12 分)
已知函数 2( ) 2 ln 1f x ax ax x a R , .
(1)当 1
4a 时,求 ( )f x 的单调区间及极值;
(2)若 a 为整数,且不等式 ( )f x x≥ 对任意 (0 )x , 恒成立,求 a 的最小值.
(二)选考题:共 10 分。请考生在第 22、23 题中任选一题作答。如果多做,则按所做的第一题计分。
22.[选修 4-4:坐标系与参数方程](10 分)
在直角坐标系 xOy 中,曲线 C 的参数方程为 2 2cos
3 2sin
x
y
( 为参数),以原点 O 为极点, x轴正半轴
为极轴建立极坐标系,直线 l 的极坐标方程为 (4sin 3cos ) a ,且直线 l 与曲线C 有两个不同的交点.
(1)求实数 a 的取值范围;
(2)已知 M 为曲线 C 上一点,且曲线C 在点 M 处的切线与直线 l 垂直,求点 M 的直角坐标.
23.[选修 4-5:不等式选讲](10 分)
已知函数 ( ) 2| | | 2|f x x x 的最小值为 m .
(1)求 m 的值;
(2)若实数 a b, 满足 2 2a b m ,求 2 2
1 1
1 2a b
的最小值.
5 月调研测试卷(文科数学)第 5页 共 8 页
2020 年普通高等学校招生全国统一考试
5 月调研测试卷 文科数学
参考答案
一、选择题
1~6 BCBBDB 7~12 CBABBA
第 7 题提示:由题知, 2 1 2 1 2 12 2 2
b a b b a b a
a b a b a b
≥ ,当且仅当
2
b a
a b
即 2 2 2 2 2a b , 时等号成立,故选 C.
第 8 题提示:不妨设 2AB ,则 2sin cos
2
1 2( )
, , 1 2sin 2 ( )2 2
, ,
故 3 5( ) ( )6 4 4 6
, , ,故 16
6P
,故选 B.
第 9 题提示:由 | |x
xy e
为奇函数可排除 C 选项,当 0x 时, 1
x
xy e
,故 x
xy e
在 (0 1), 上单增,(1 ) ,
上单减,故选 A.
第 10 题提示:由 ( )f x 为奇函数知 3 3( ) ( )4 4f x f x , 3 3( ) ( )4 4f x f x ,即 3( ) ( )2f x f x ,
3( 3) ( ) ( )2f x f x f x , ( )f x 是周期为 3 的周期函数,
故 2
1 3(100) (1) ( ) log2 2f f f m ,即 2 2
3log log 32 m , 1m ,故选 B.
第 11 题提示:原式 2 2
sin sin
sin sin cos sin sin cos coscos cos
sin sin sin sin sin( ) sin( )cos cos cos
A B
A B C A B C ab CA B
C A B C A B C c
C A B
,
又 2 2 29 9 19a b c , 2 2 2 2102 cos 9ab C a b c c ,故原式 5
9
,故选 B.
第 12 题提示: 2sin [ 2 2]y a x a a , ,由题知在区间 [ 2 2]a a , 内存在两数之积为 1 ,故只需
( 2)( 2) 1a a ≤ ,即 3 3a- ≤ ≤ ,故选 A.
二、填空题
13. 4 14. 945 2
15.192 16. 4 5
5
第 14 题提示:由三视图可知该几何体是一个长方体中挖去一个 1
8
球,
如图所示, 31 4 93 3 5 3 458 3 2V .
第 15 题提示:设公差为 d ,由题知 2
4 4 4( 2 )( 4 )a a d a d ,
即 4 4a d ,故 1a d , na nd , 3 63 6a d a d , ,
故此等比数列首项为3d 、公比为 2 ,
5 月调研测试卷(文科数学)第 6页 共 8 页
因此
5
63 2 192ba d d ,故 5 192b .
第 16 题提示:由题知| | 32P
pFP x p , 5
2Px p ,设点 (0 1)A , ,由题知 AP AF ,
即 11 = 15
2 2
Py
p p
- , 5Py p - , 2 5
5p ,故所求距离为 5 4 5
2 2 5
p p .
三、解答题
17.(12 分)
解:(1) ( ) sin 2 3(1 cos2 ) 3 2sin(2 )3f x x x x , ……2 分
由 2 2 22 3 2k x k ≤ ≤ 得 5
12 12k x k ≤ ≤ , ……4 分
故 ( )f x 在 5[ ]12 12k k , 上单增,在 5 11[ ]12 12k k , 上单减, k Z ;……6 分
(2) ( ) 2sin( ) 32 3
Af A ,则 3sin( )3 2A , (0 )A , ,
3 3A ,即 2
3A ,…8 分
由正弦定理得 1 3
sin 3
2
C
, 1sin 2C ,
6C ,故
6B ,
1 3sin2 4ABCS ac B . ……12 分
18.(12 分)
解:(1)由题知,第二、四组的频率均为 0.2 ,第三组频率为10a ,则第五组的频率为 1 21 3 0.2 0.2 15 15
,
故 2 20.2 10 15a ,解得 0.03a ; ……6 分
(2)由(1)知最后三组的频率分别为 1 2 1
5 15 15
, , ,故所抽取的 6 人中最后三组分别有 3 人、 2 人、1人,
从中随机抽出 2 人,有 15 种不同结果,其中两人来自同一组的结果有 4 种,所求概率为 4
15 . …12 分
19.(12 分)
解:(1)取 AC 的中点 F ,连接 BF EF, ,则 1/ /EF AA 且 1
1
2EF AA ,
/ /EF DB 且 EF DB ,故 / /DE BF ,
由 ABC 为等腰三角形知 BF AC ,
又 1AA 面 ABC , 1A A BF ,
BF 面 1 1ACC A ,
DE 平面 1 1ACC A ;……6 分
(2) 5AD CD , 2 2AC , 6ACDS , 2ACES , 2DE BF ,
设点 E 到平面 ACD 的距离为 h ,由 E ACD D ACEV V 得 1 16 2 23 3h ,
6
3h ,即点 E 到平面 ACD 的距离为 6
3 . ……12 分
1B1A
C
BA
E D
1C
F
5 月调研测试卷(文科数学)第 7页 共 8 页
20.(12 分)
解:(1)由题知 2
2
1 3 2| | ( 1) 2 2PF c ,故 1c ,又 2 2
1 1 12a b
, 2 2a , 2 1b ,
所以椭圆C 的方程为
2
2 12
x y ; ……4 分
(2)设 1 1 2 2 0 0( ) ( ) ( )A x y B x y M x y, , , , , ,则
2
21
1 12
x y ,
2
22
2 12
x y ,
相减得 1 2
1 2( ) 02 AB
x x y y k ,由(1)知 2 (1 0)F , ,故 0 0
0
0
02 1
x yy x
,
即 2 2
0 0 02 0x x y ①, ……7 分
由 3ON OM 得 0 0(3 3 )N x y, ,由点 N 在椭圆C 上得
2
20
0
9 9 12
x y ②,
由①②得 0 0
2 7
9 9x y , ……10 分
7
9: ( 1)2 19
l y x
即 7 ( 1)7y x . ……12 分
21.(12 分)
解:(1) 21 1( ) ln 14 2f x x x x , 1 1 1 ( 1)( 2)( ) 2 2 2
x xf x x x x
( 0x ), ( ) 0 1f x x ,故
( )f x 在 (0 1), 上单减,在 (1 ) , 上单增, ( )f x 在 1x 处取得极小值 1
4
,无极大值;…4 分
(2) 2( ) (2 1) ln 1 0f x x ax a x x ≥ ≥ ,设 2( ) (2 1) ln 1g x ax a x x ,
( ) 0g x ≥ 在 (0 )x , 上恒成立, (1) 3 2 0g a ≥ ,即 2
3a≥ ,
1 (2 1)( 1)( ) 2 (2 1) ax xg x ax a x x
,
故 ( )g x 在 1(0 )2a
, 上单减,在 1( )2a
, 上单增, 1 1 1( ) ( ) ln2 4 2g x g a a a
≥ , ……8 分
由题得 1 1ln 04 2a a
≥ ,即 1ln 2 04a a
≥ ,设 1( ) ln 2h x x x
,则 2
1 1( ) 02h x x x
,
( )h x 单增,又 1(1) 02h , 1(2) ln 2 04h ,则存在 0 (1 2)x , 使得 0( ) 0h x ,故
0(2 ) 0 2h a a x≥ ≥ ,即 0
1
2a x≥ ,所以整数 a 的最小值为1. ……12 分
22.(10 分)
解:(1)曲线C 的普通方程为 2 2( 2) ( 3) 4x y ,直线l 的直角坐标方程为 4 3y x a ,由直线l 与圆C 有
两个交点知 | 6 12 | 25
a ,解得8 28a ; ……5 分
(2)设圆C 的圆心为 1O ,由圆C 的参数方程可设点 0 0(2 2cos 3 2sin )M , ,由题知 1 / /O M l ,
0 0
4 3cos sin5 5
, ,或 0 0
4 3cos sin5 5
, ,故点 2 21( )5 5M , ,或 18 9( )5 5
, . ……10 分
5 月调研测试卷(文科数学)第 8页 共 8 页
23.(10 分)
解:(1) ( ) | | | | | 2 | | | | ( 2) | | | 2 2f x x x x x x x x ≥ ≥ ,当且仅当 0x 时等号成立,
故 2m ; ……5 分
(2) 2 2 2a b ,由柯西不等式得 2 2 2
2 2
1 1( )(1 2 ) (1 1)1 2 a ba b
≥ ,
当且仅当 2 23 1
2 2a b , 时等号成立, 2 2 2 2
1 1 4 4
1 2 3 5a b a b
≥ ,
故 2 2
1 1
1 2a b
的最小值为 4
5 . ……10 分