- 822.00 KB
- 2024-05-26 发布
福建省闽侯第六中学 8 2017-2018 学年高二上学期期末考试
试题数学(理)
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.抛物线的准线方程为( )
A. B. C. D.
2.设等差数列的前项和为,已知,则( )=
A.-27 B.27 C.-54 D.54
3.焦点在轴上,虚轴长为12,离心率为的双曲线标准方程是( )
A. B. C. D.
4.已知双曲线的一条渐近线方程为,则该双曲线的离心率是( )
A. B. C. D.
5.直三棱柱中,分别是,的中点,,则与所成角的余弦值为( )
A. B. C. D.
6.已知等比数列中,,则其前三项的和的取值范围是( )
A. B. C. D.
7.展开式中的系数为( )
A.92 B.576 C. 192 D.384
8. 60° 的二面角的棱上有两点,直线
分别在这个二面角的两个半平面内,且都垂直于,已知,则的长为( )
A. B. C. D.
9.已知不等式对任意恒成立,则实数 的取值范围是( )
A. B. C. D.
10.设椭圆与函数的图象相交于两点,点为椭圆上异于的动点,若直线的斜率取值范围是,则直线的斜率取值范围是( )
A. B. C. D.
11.设数列的前项和,若,且,则等于( )
A.5048 B.5050 C.10098 D.10100
12.已知双曲线的上焦点为,是双曲线下支上的一点,线段与圆相切于点,且,则双曲线的渐近线方程为( )
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13.已知命题:,使,则是 .
14.已知正项等比数列的公比为2,若,则的最小值等于 .
15.已知是抛物线上一点,为其焦点,点在圆上,则的最小值是 .
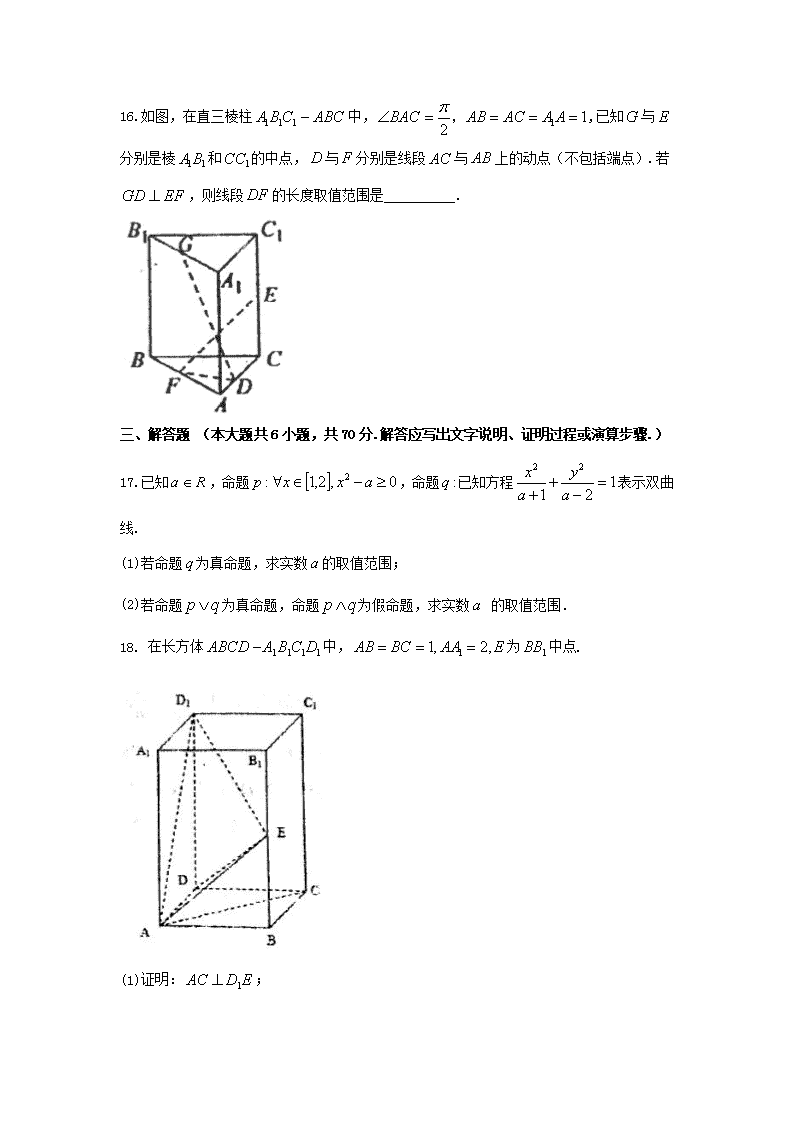
16.如图,在直三棱柱中,,已知与分别是棱和的中点,与分别是线段与上的动点(不包括端点).若,则线段的长度取值范围是 .
三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17. 已知,命题,命题已知方程表示双曲线.
(1)若命题为真命题,求实数的取值范围;
(2)若命题为真命题,命题为假命题,求实数 的取值范围.
18. 在长方体中,为中点.
(1)证明:;
(2)求与平面所成角的正弦值.
19. 已知数列满足,.
(1)求证:数列是等比数列;
(2)若数列是单调递增数列,求实数的取值范围.
20. 如图,四棱锥中,底面为矩形,侧面为正三角形,且平面平面,为中点,.
(1)求证:平面平面;
(2)若二面角的平面角大小满足,求四棱锥的体积.
21. 已知过抛物线的焦点,斜率为的直线交抛物线于两点,且.
(1)求该抛物线的方程;
(2)过点任意作互相垂直的两条直线,分别交曲线于点和.设线段的中点分别为,求证:直线恒过一个定点.
22.已知椭圆的中心在原点,焦点在轴上,左右焦点分别为,且,点在椭圆上.
(1)求椭圆的方程;
(2)过的直线与椭圆相较于两点,且的面积为,求直线的方程.
试卷答案
一、选择题
1-5: DADAA 6-10:DBBBD 11、12:CB
二、填空题
13. 14. 15.6 16.
三、解答题
17.解:(1)若为真命题时:,,;
(2)若为真命题时:,,
为真命题,为假命题,则一真一假,即
或,
解得或,的范围为 .
18.(1)证明:连结
∵是长方体,∴平面
又平面中,
在长方形中,
又,∴平面,
而平面,∴
(2)如图,以为坐标原点,以所在的直线为轴建立空间直角坐标系,则
,
设平面的法向量为,则
令,则
∴
所以与平面所成角的正弦值为.
19.解(1)因为数列满足,所以,
即,又,所以,
所以数列是以 2 为首项,公比为 2 的等比数列.
(2)由(1)可得,所以,
因为符合,所以.
因为数列是单调递增数列,所以,即,
化为,所以.
20.证明:(1)取中点为,中点为,
由侧面为正三角形,且平面平面,得平面,故,
又,则平面,
又,则,
又是中点,则,
由线面垂直的判定定平面.
又平面,故平面平面.
(2)如图,以为坐标原点,以所在的直线为轴建立空间直角坐标系,则令,则
由(1)知为平面的法向量,
令为平面的法向量,由于,
故即,解得,故,
由,解得.
故四棱锥的体积.
21.解:(1)抛物线的焦点,∴直线的方程为:
联立方程组,消元得:
,解得.
∵,∴抛物线的方程为:.
(2)设 两点坐标分别为,则点的坐标为
由题意可设直线的方程为.
由,得.
因为直线与曲线于两点,所以.
所以点得坐标为.
由题知,直线的斜率为,同理可得点的坐标为.
当时,有,此时直线的斜率.
所以,直线的方程为,整理得.
于是,直线恒过定点;
当时,直线的方程为,也过点.
综上所述,直线恒过定点.
22.解:(1)
(2)设代入,得
,∴,∴
,故所求直线方程为: