- 680.50 KB
- 2024-05-17 发布
泰安长城中学2016—2017学年第二学期期中考试
高二数学文科试卷
说明:1.本试卷分卷Ⅰ和卷Ⅱ两部分,卷Ⅰ为选择题,卷Ⅱ为非选择题,考试时间为120
分钟,满分为150分。
2.将卷Ⅰ答案用2B铅涂在答题卡上,卷Ⅱ用蓝黑钢笔或圆珠笔答在答题纸上。
卷Ⅰ(选择题 共60分)
一. 选择题:本大题共12小题,每小题5分,共60分.
1.如果集合,那么( )
A、 B、 C、 D、
2.命题“且,”的否定是( )
A、且, B、且,
C、且, D、且,
3.下列函数中,既不是奇函数,也不是偶函数的是( )
A. B. C. D.
4.设为虚数单位,复数,,则复数在复平面上对应的点在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5. 用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是( )。
(A)假设三内角都不大于60度; (B) 假设三内角都大于60度;
(C) 假设三内角至多有一个大于60度; (D) 假设三内角至多有两个大于60度。
6.已知x与y之间的一组数据:则y与x的线性回归方程为y=bx+a必过( )
x
0
1
2
3
y
1
3
5
7
A、(1.5,4)点 B、(1.5,0)点 C、(1,2)点 D、(2,2)点
7.要证成立,只需证
A. B.
C. D.
8.“”是“函数在区间上为增函数”的( )
A充分不必要条件 B 必要不充分条件 C 充要条件 D 既不充分也不必要条件
9.定义在R上的偶函数,满足,且在区间上为递增,则( )
A. B.
C. D.
10. 已知函数的导函数为,且满足,则=( )
A. B. C. D.
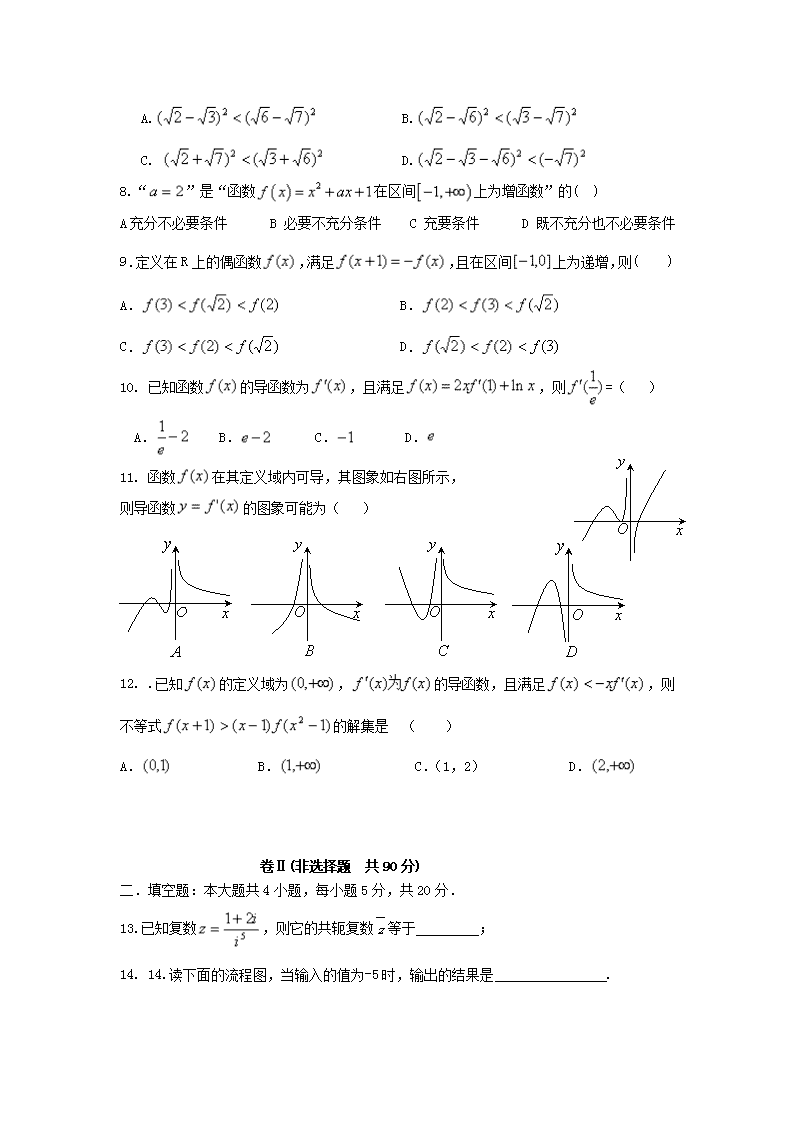
11. 函数在其定义域内可导,其图象如右图所示,
则导函数的图象可能为( )
12. .已知的定义域为,的导函数,且满足,则不等式的解集是 ( )
A. B. C.(1,2) D.
卷Ⅱ(非选择题 共90分)
二.填空题:本大题共4小题,每小题5分,共20分.
13.已知复数,则它的共轭复数等于 ;
14. 14.读下面的流程图,当输入的值为-5时,输出的结果是 .
16.如图给出了一个“直角三角形数阵”:满足每一列成等差数列,从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N*),则a88= .
16.已知函数f(x)=4x3+ax2+bx+5在x=-1与x=处有极值, 则函数的单调递减区间为______________
三. 解答题:本大题共6小题,共70分.
17. (10分)已知复数
(1) 求复数 (2)若求实数的值
18.(12分)已知命题,命题
(1)若是的充分条件,求实数的取值范围
(2)若,为真命题,为假命题,求实数的取值范围
19..(12分)为调查某地区老人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别
是否需要志愿者
男
女
需要
40
30
不需要
160
270
(1) 估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(1) 请根据上面的数据分析该地区的老年人需要志愿者提供帮助与性别有关吗?
0.10
0.05
0.010
2.706
3.841
6.635
20.(12分)已知函数满足①;②。
(1)求函数的解析表达式;
(2)若对任意,都有成立,求实数的取值范围。
21.某厂生产某种产品的固定成本(固定投入)为2500元,已知每生产x件这样的产品需要再增加可变成本C(x)=200x+x3(元),若生产出的产品都能以每件500元售出,要使利润最大,该厂应生产多少件这种产品?最大利润是多少?
22.设,函数.
(1)若,求曲线在点处的切线方程;
(2)求函数的单调区间;
(3)当时,求函数在上的最小值.
泰安长城中学2016—2017学年第二学期期中考试
高二数学文科试卷(参考答案)
一.选择题(每小题5分,共60分)
1
2
3
4
5
6
7
8
9
10
11
12
D
D
D
A
B
A
C
A
A
B
C
D
二.填空题(每小题5分,共20分)
13. 2+i 14. 2 15. 16. (-1,)
三.17.(10分)
解:(1)==
(2)把代入已知方程,得
整理,得,
18.(12分)
(1)对于,对于
由已知,,,
(2)若真:,若真:
由已知,、一真一假
①若真假,则,无解;
②若假真,则,的取值范围为
19.(12分)解:(1)调查的500位老年人中有70位需要志愿者提供帮助,因此该地区老年人中,需要帮助的老年人的比例的估算值为
(2)根据表中数据计算得:。
由于9.967>6.635,所以有99%的把握认为该地区的老年人是否需要帮助与性别有关。
20.(12分)解:(1)即,又,又,。
所以
(2)法一:设,则由已知得:
当即时,,此时;
当即时,,解得:无解;
当即时,,此时无解。
综上所述,的取值范围为。
法二:由已知得,在上恒成立。由于在上单调递增,所以,故即。
21.(12分)解:设该厂生产x件这种产品利润为L(x)
则L(x)=500x-2 500-C(x)
=500x-2 500-
=300x-x3-2 500(x∈N)
令L′(x)=300-x2=0,得x=60(件)
又当0≤x<60时,L′(x)>0
x>60时, L′(x)<0
所以x=60是L(x)的极大值点,也是最大值点.
所以当x=60时,L(x)=9 500元.
答:要使利润最大,该厂应生产60件这种产品,最大利润为9 500元.
22.(12分)解:在区间上,,
(1)当时,,则切线方程为,即;
(2)①当时,,故函数为增函数,即函数的单调递增区间为;
②当时,令,可得,
当时,;当,,
故函数的单调递增区间为,单调递减区间为;
(3)①当时,即当时,函数在区间上是减函数,
的最小值是;
②当时,即当时,函数在区间上是增函数,
的最小值是;
③当时,即当时,函数在上是增函数,在上是减函数,
所以的最小值产生于与之间,又,
当时,最小值为;
当时,最小值为,
综上所述,当时,函数的最小值是,
当时,函数的最小值是.