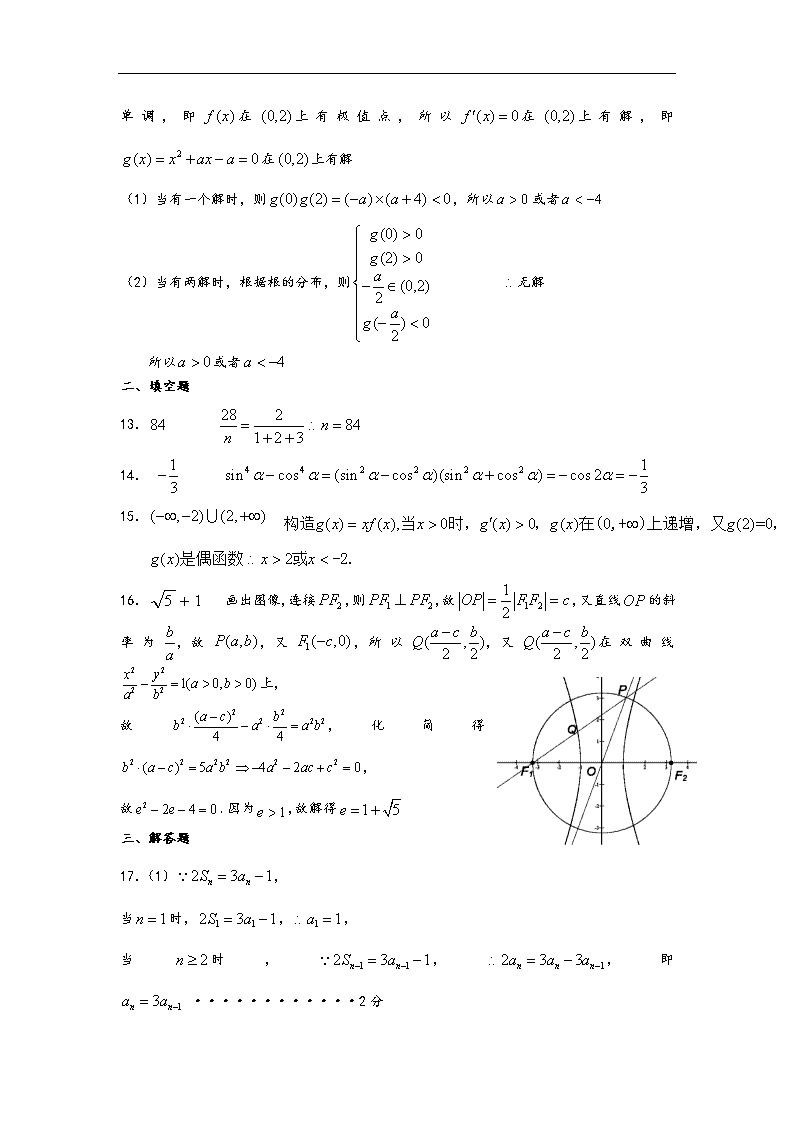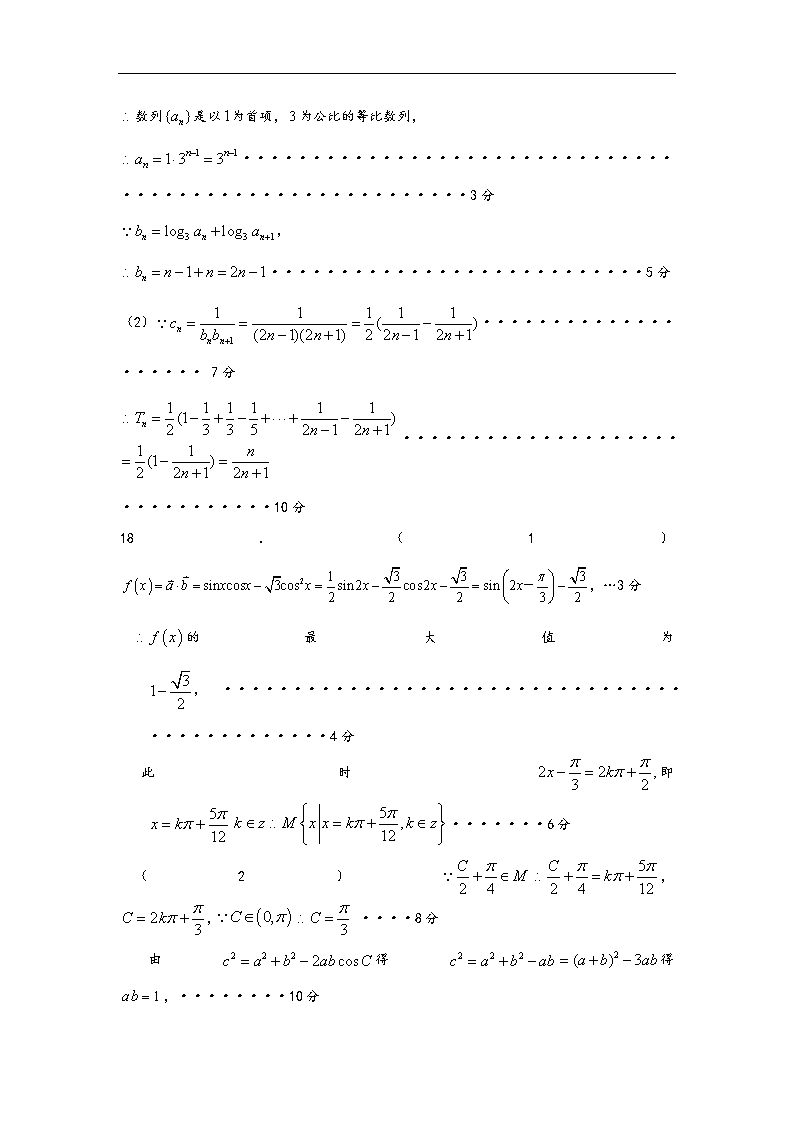A佳经典联考2019-2020学年高二1月期末联考数学参考答案 9页

A佳经典•高二期末考试试题 数学 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ D A B C A B C D B A C B 一、选择题 ‎1．D ，，则 ‎2．A ‎ ‎3．B ，‎ ‎4．C ‎ ‎5．A ‎ ‎6．B ‎ ‎7．C ‎8．D ‎ ‎9．B ‎ ‎ ‎ ‎10．A 的周期，在同一坐标系下分别画出和的图像 ‎11.C 是的中点，由中位线可知，‎ 又， ‎ ‎12．B ，在 上不单调，即在上有极值点，所以在上有解，即在上有解 （1） 当有一个解时，则，所以或者 （2） 当有两解时，根据根的分布，则 无解 所以或者 二、 填空题 ‎13． ‎ ‎14． ‎ ‎15．‎ ‎16． 画出图像,连接,则,故,又直线的斜率为,故,又,所以,又在双曲线上,‎ 故,化简得,‎ 故.因为,故解得 ‎ 三、 解答题 ‎17．（1），‎ 当时，，， ‎ 当时，，，即 ············2分 数列是以为首项，为公比的等比数列，‎ ‎························································3分 ‎，···························5分 （2） ‎···················· 7分 ‎·······························10分 ‎18．（1），…3分 的最大值为， ··············································4分 ‎ 此时即·······6分 ‎（2），, ····8分 由得得，········10分 故 ·············································· 12分 ‎19．解法一：（1）为矩形，且平面平面，‎ 平面平面，在中，，‎ 在梯形中，，从而．‎ 在中，，可知，‎ 在中，，可知，‎ 又，平面··································6分 ‎（2）取的中点，连接，由知，‎ 由知，为二面角的平面角．······9分 由（1）知平面，，又，‎ ‎ ，···············11分 ‎ ············12分 解法二：（2）为矩形，且平面平面，平面，‎ 又，所以可以以为原点建立如图所示空间直角坐标系，则 ‎，‎ ‎，‎ 设平面的法向量为，则 ，‎ 令，得．·················································8分 设平面的法向量为，则，‎ 令，得．··················································10分 ‎，·········································11分 ‎ 所以二面角的正弦值为． ·································12分 ‎20．（1）设“从学习时间的6个数据中随机选取2个数据，求这2个数据不相邻”为事件，‎ 这6个数据为 抽取2个数据的基本事件有，共种，‎ 其中相邻的有，共种，‎ ‎··········································3分 所以······················································5分 ‎（2）前四组数据为：‎ 学习时间（第天）‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 当天得分 ‎17‎ ‎20‎ ‎19‎ ‎24‎ ‎ ······6分 ‎ ·······························8分 ‎ ···························10分 当时，，此时成立 当时，，此时成立 为恰当回归方程.···········································12分 ‎21．（1） ····················································4分 ‎（2）若直线斜率不存在，则直线方程为，‎ 此时，·························································5分 若直线斜率存在，设直线方程为，，‎ 联立，得：‎ ‎∴ ······································7分 ‎∴∴···················8分 ‎∵直线与圆相切，∴，即·····················9分 ‎∴‎ 当时，‎ 当时，，·······························11分 当且仅当时，等号成立 ∴·······················12分 ‎22． （1），定义域为 ····································1分 当时，，所以在区间上为减函数，‎ 当时，，所以在区间上为增函数，··················2分 所以，无极小值 ； ‎ 的递减区间，递增区间 ·······························4分 ‎（2）因为，所以················· 6分 ① 当时，，在上单调递减，‎ 由, 所以，即，得 ····················8分 ① 当时，，在上单调递增，‎ 所以，即，得 ·································10分 ‎③ 当时，‎ 在，，在上单调递减，在，，在上单调递增 ‎ 所以 即 （） ‎ 由（Ⅰ）知在上单调递减 故，而，所以不等式（）无解 ‎ 综上所述，． ·····································12分 ‎