- 1.23 MB
- 2024-05-03 发布
宜昌市部分重点中学2016-2017学年第一学期
高二年级期末考试试卷 数 学(文) 试 卷
考试时间:120分钟 满分:150分
一、选择题(本大题共12小题,每小题5分,共60分)
1.复数的共轭复数是( )
A B C D
2.命题:“,”的否定为:( )
A., B.,
C., D.,
3.在长为3的线段上任取一点,则点与线段两端点的距离都大于1的概率等于( )
A. B. C. D.
4. 经过点并且在两个坐标轴上的截距的绝对值相等的直线方程为( )
A.或 B.,
C.,或 D.,或,或
5.某产品的广告费用与销售额的不完整统计数据如下表:
广告费用(万元)
3
4
5
销售额(万元)
22
28
m
若已知回归直线方程为,则表中的值为
A. B.39 C.38 D.37
6.已知约束条件,若目标函数在且只在点处取得最大值,则的取值范围为( )
A. B. C. D.
7.已知直线mx+4y-2=0和2x-5y+n=0互相垂直,且垂足为(1,p),则m-n+p的值是( )
A.24 B.20 C.0 D.-4
8.如图,给出的是计算的值的程序框图,其中判
断框内不能填入( ).
A. i≤2017? B.i<2018? C. i≤2015? D.i≤2016?
9.“m=1”是“直线与直线平行”的( )
1
2
2
正视图
侧视图
俯视图
1
1
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
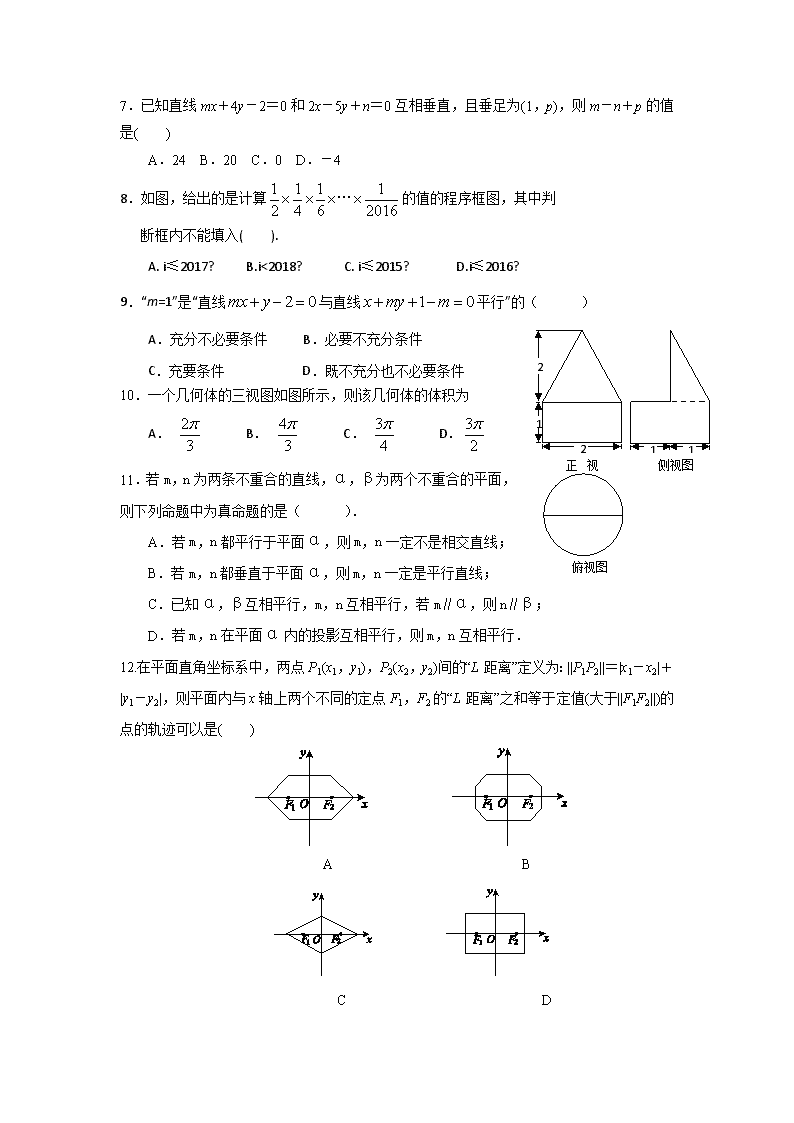
10.一个几何体的三视图如图所示,则该几何体的体积为
A. B. C. D.
11.若m,n为两条不重合的直线,α,β为两个不重合的平面,
则下列命题中为真命题的是( ).
A.若m,n都平行于平面α,则m,n一定不是相交直线;
B.若m,n都垂直于平面α,则m,n一定是平行直线;
C.已知α,β互相平行,m,n互相平行,若m∥α,则n∥β;
D.若m,n在平面α内的投影互相平行,则m,n互相平行.
12.在平面直角坐标系中,两点P1(x1,y1),P2(x2,y2)间的“L距离”定义为:||P1P2||=|x1-x2|+|y1-y2|,则平面内与x轴上两个不同的定点F1,F2的“L距离”之和等于定值(大于||F1F2||)的点的轨迹可以是( )
A B
C D
二、填空题(本大题共4小题,每小题5分,共20分)
13. 在空间直角坐标系中,点A(1,3,﹣2),B(﹣2,3,2),则A,B两点间的距离为
14. 为了对某课题进行研究,用分层抽样方法从三所高校A,B,C的相关人员中,抽取若干人组成研究小组,有关数据见表(单位:人).则x= ,y= ;
高校
相关人数
抽取人数
A
18
x
B
36
2
C
54
y
若从高校B,C抽取的人中选2人作专题发言,则这2人都来自高校C的概率P= .
15. 将某选手的6个得分去掉1个最高分,去掉一个最低分,4个剩余分数的平均分为91.现场作的6个分数的茎叶图后来有1个数据模糊,无法辨认,在图中以表示:
8 7
9 3 0 0 1
则4个剩余分数的方差为 .
16. 已知双曲线 (,)的一条渐近线为,一个焦点为,则 ;
三、解答题(17小题 10分,18—22小题每题12分;共70分)
17. (本小题10分)我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5), [0.5,1),……[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(I)求直方图中的a值;
(II)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数.说明理由;
(Ⅲ)估计居民月均用水量的中位数.
18. (本小题12分)已知命题:,不等式恒成立,命题:椭圆的焦点在轴上.若命题p∨q为真命题,求实数m的取值范围
19. (本小题满分12分) 的内角A,B,C的对边分别为a,b,c,已知
(I)求C;
(II)若的面积为,求的周长
20. (本小题满分l2分)如图,四棱锥中,平面,,,,为线段上一点,,为
的中点.
(I)证明平面;
(II)求四面体的体积.
21.(本小题满分l2分) 已知袋子中放有大小和形状相同的小球若干,其中标号为0的小球1个,标号为1的小球1个,标号为2的小球个.若从袋子中随机抽取1个小球,取到标号为2的小球的概率是
(1)求的值
(2)从袋子中不放回地随机抽取2个小球,记第一次取出的小球标号为,第二次取出的小球标号为
(i)记“”为事件,求事件的概率;
(ii)在区间[0,2]内任取2个实数,求事件“恒成立”的概率
22.(本小题满分12分)已知椭圆的左右焦点分别为F1和F2,由4个点M(-a,b)、N(a,b)、F2和F1组成了一个高为,面积为的等腰梯形.
(1)求椭圆的方程;
(2)过点F1的直线和椭圆交于两点A、B,求F2AB面积的最大值.
数学试卷参考答案
1.D2.B 3. D 4. D 5. A 6. A 7. B 8.C 9.C 10 .B 11. B 12. A
13.5 14.1(1分),3(1分),(3分) 15.
16.. a=1(2分) b=2(3分 )
17. 答案】(Ⅰ);(Ⅱ)36000;(Ⅲ)2.04.
【解析】(Ⅰ)由高×组距=频率,计算每组中的频率,因为所有频率之和为1,计算出a的值;(Ⅱ)利用高×组距=频率,先计算出每人月均用水量不低于3吨的频率,再利用频率×样本总数=频数,计算所求人数;(Ⅲ)将前5组的频率之和与前4组的频率之和进行比较,得出2≤x<2.5,再进行计算.
试题解析:(Ⅰ)由频率分布直方图,可知:月用水量在[0,0.5]的频率为0.08×0.5=0.04.(1分)
同理,在[0.5,1),(1.5,2],[2,2.5),[3,3.5),[3.5,4),[4,4.5)等组的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.(3分)
由1–(0.04+0.08+0.21+.025+0.06+0.04+0.02)=0.5×a+0.5×a,(4分)
解得a=0.30.(5分)
(12分)
(11分)
(10分)
(9分)
第2问(8分)
考点:频率分布直方图、频率、频数的计算公式
18. .解:p真:, ∴ ……3分
q真: ∴ ……6分
若p∨q为假命题 ,则 ……11分
∴ 实数m的取值范围是 ……12分
19(1)
由正弦定理得:
∵,
∴
∴,
∵
∴
⑵ 由余弦定理得:
∴
∴
∴周长为
20【答案】(Ⅰ)见解析;(Ⅱ).
【解析】
(Ⅱ)因为平面,为的中点,
所以到平面的距离为. ....9分
取的中点,连结.由得,.
由得到的距离为,故,
所以四面体的体积. .....12分
21.解:(1)依题意,得. ……3分
(2)(i)记标号为0的小球为,标号为1的小球为,标号为2的小球为,则取出2个小球的可能情况有:
,
共12种,其中满足“”的有4种;,
∴ 所求概率为 …… 7分
(ii)记“恒成立”为事件B,则事件B “恒成立”
…8分
则全部结果所构成的区域为=, ……9分
而事件B构成区域 ,
∴ 所求的概率为 ……12分
22解:(1)由条件,得b=,且,所以a+c=3. ……………2分
又,解得a=2,c=1.所以椭圆的方程. ………4分
(2)显然,直线的斜率不能为0,设直线方程为x=my-1,直线与椭圆交于A(x1,y1),B(x2,y2).
联立方程,消去x得, ,
因为直线过椭圆内的点,无论m为何值,直线和椭圆总相交.
…………………6分
=………………8分
……10分
令,设,易知时,函数单调递减,函数单调递增,所以当t==1即m=0时,
取最大值3.…………………12分