- 1.21 MB
- 2024-04-18 发布
中山市第一中学2017-2018学年高二年级第二次统测
理科数学试卷
命题人: 审题人:
一、选择题(本大题共12小题,共60分)
1.下列说法正确的是( )
A.由归纳推理得到的结论一定正确
B.由类比推理得到的结论一定正确
C.由合情推理得到的结论一定正确
D. 演绎推理在前提和推理形式都正确的前提下,得到的结论一定正确
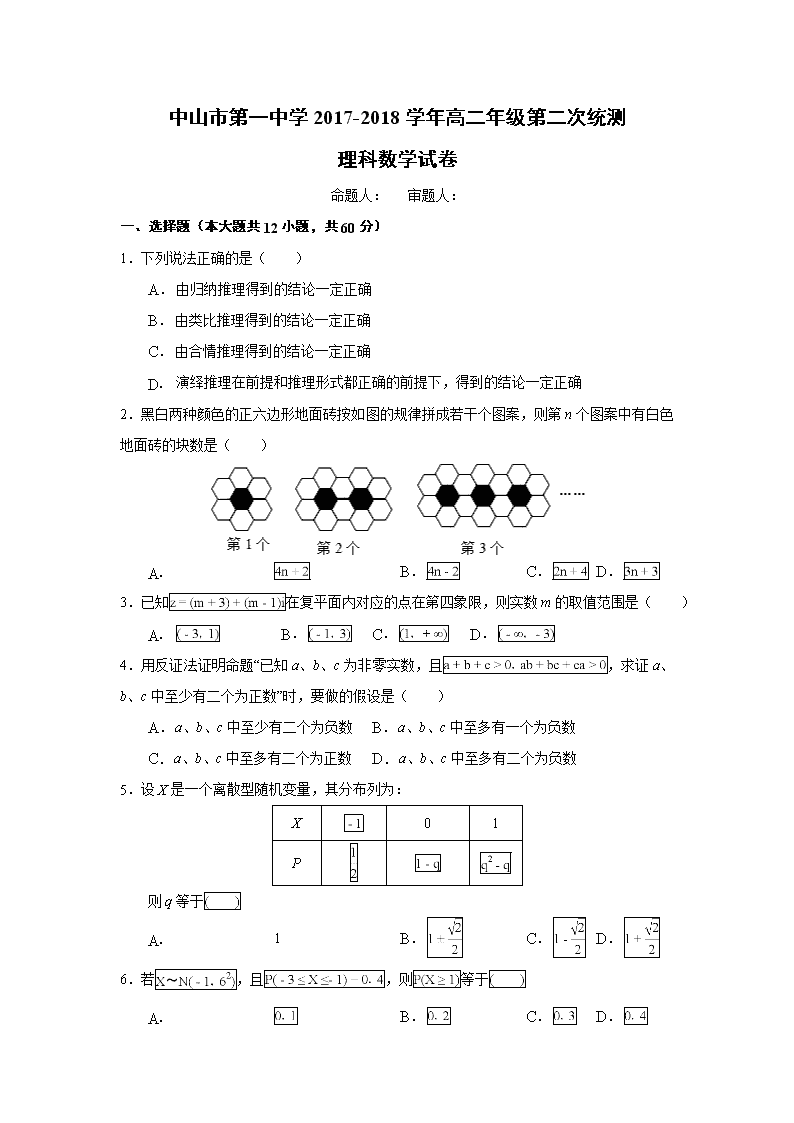
2.黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案,则第n个图案中有白色地面砖的块数是( )
A. B. C. D.
3.已知在复平面内对应的点在第四象限,则实数m的取值范围是( )
A. B. C. D.
4.用反证法证明命题“已知a、b、c为非零实数,且,求证a、b、c中至少有二个为正数”时,要做的假设是( )
A.a、b、c中至少有二个为负数 B.a、b、c中至多有一个为负数
C.a、b、c中至多有二个为正数 D.a、b、c中至多有二个为负数
5.设X是一个离散型随机变量,其分布列为:
X
0
1
P
则q等于
A. 1 B. C. D.
6.若,且,则等于
A. B. C. D.
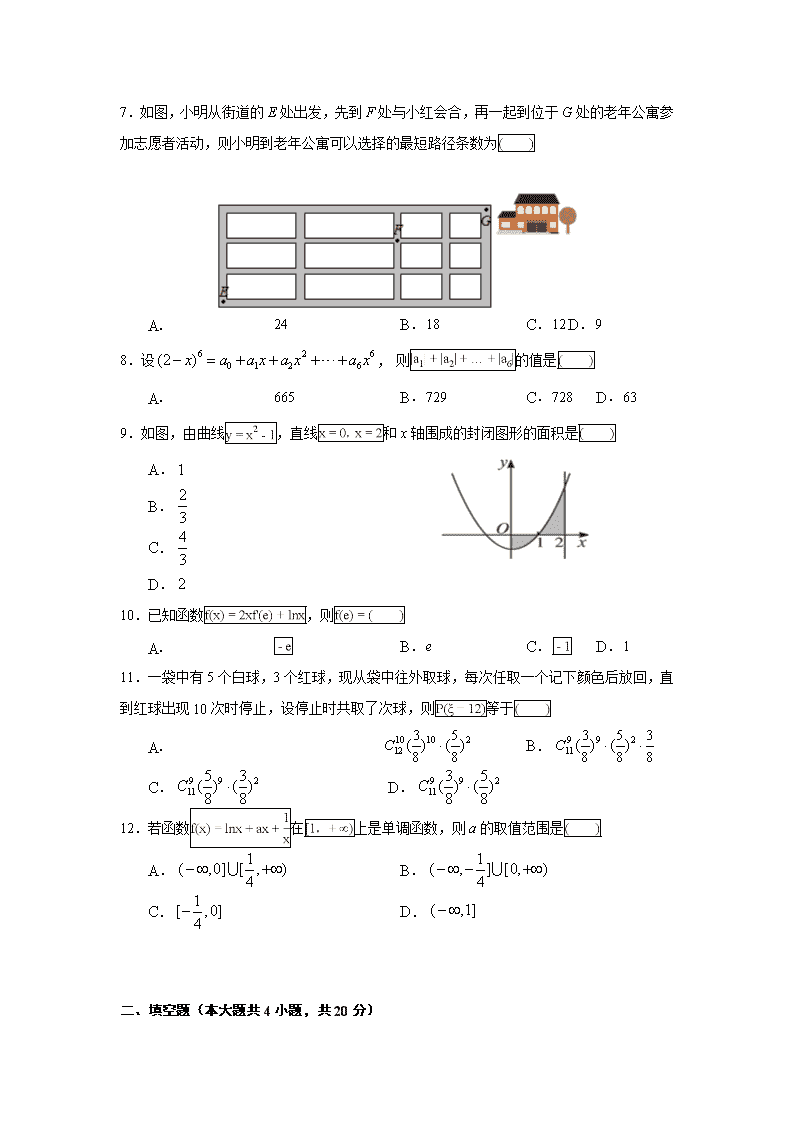
7.如图,小明从街道的E处出发,先到F处与小红会合,再一起到位于G处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为
A. 24 B.18 C.12 D.9
8.设,则的值是
A. 665 B.729 C.728 D.63
9.如图,由曲线,直线和x轴围成的封闭图形的面积是
A.
B.
C.
D.
10.已知函数,则
A. B.e C. D.1
11.一袋中有5个白球,3个红球,现从袋中往外取球,每次任取一个记下颜色后放回,直到红球出现10次时停止,设停止时共取了次球,则等于
A. B.
C. D.
12.若函数在上是单调函数,则a的取值范围是
A. B.
C. D.
二、填空题(本大题共4小题,共20分)
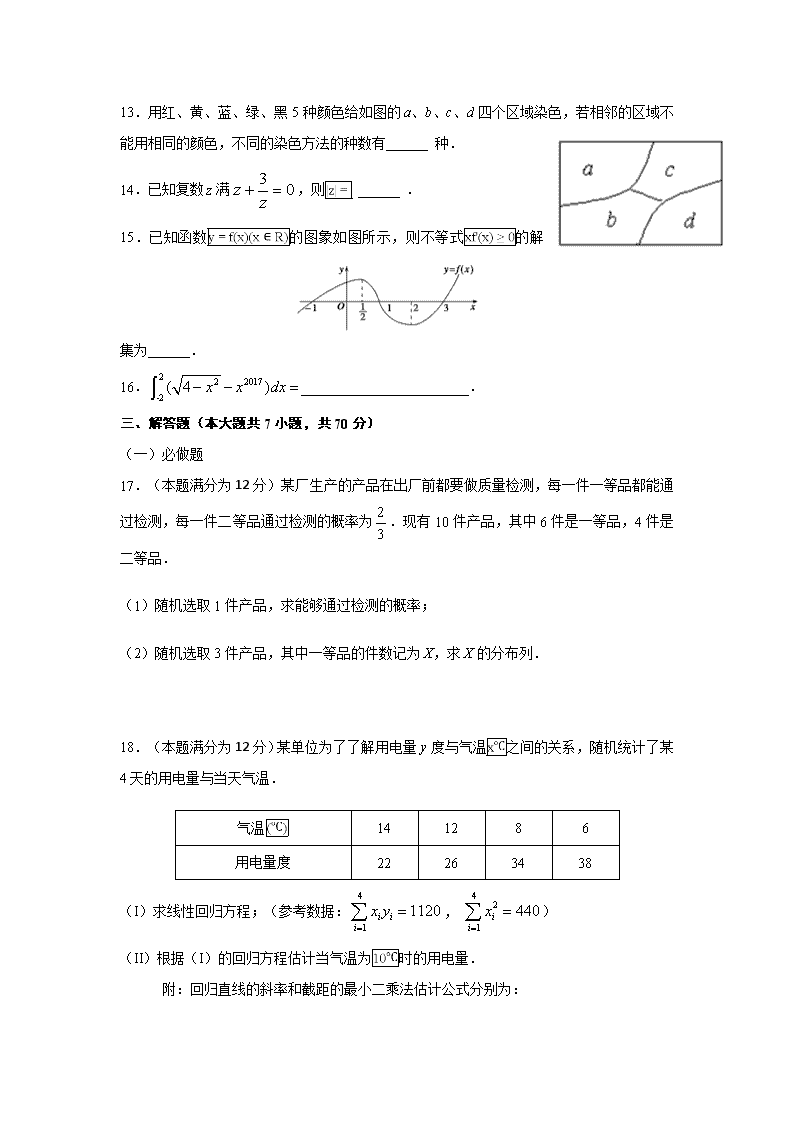
13.用红、黄、蓝、绿、黑5种颜色给如图的a、b、c、d四个区域染色,若相邻的区域不能用相同的颜色,不同的染色方法的种数有______ 种.
14.已知复数z满,则 ______ .
15.已知函数的图象如图所示,则不等式的解集为______.
16. .
三、解答题(本大题共7小题,共70分)
(一)必做题
17.(本题满分为12分)某厂生产的产品在出厂前都要做质量检测,每一件一等品都能通过检测,每一件二等品通过检测的概率为.现有10件产品,其中6件是一等品,4件是二等品.
(1)随机选取1件产品,求能够通过检测的概率;
(2)随机选取3件产品,其中一等品的件数记为X,求X的分布列.
18.(本题满分为12分)某单位为了了解用电量y度与气温之间的关系,随机统计了某4天的用电量与当天气温.
气温
14
12
8
6
用电量度
22
26
34
38
(I)求线性回归方程;(参考数据:,)
(II)根据(I)的回归方程估计当气温为时的用电量.
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
,.
19.(本题满分为12分)已知,().
(1)求并由此猜想数列的通项公式的表达式;
(2)用数学归纳法证明你的猜想.
20.(本题满分为12分)已知的展开式中,某一项的系数是它前一项系数的2倍,而等于它后一项的系数的.
(1)求该展开式中二项式系数最大的项;
(2)求展开式中系数最大的项.
21.(本题满分为12分)设函数,记.
(I)求曲线在处的切线方程;
(II)求函数的单调区间;
(III)当时,若函数没有零点,求a的取值范围.
(二)选做题(请考生从给出的22、23两题中任选一题作答,并用2B铅笔在答题卡上把所选的题号涂黑,注意所做题目必须与所涂题号一致,如果多做,则按所做的第一题计分。)
22.(本题满分为10分)已知直线l的参数方程为(为参数)
,以原点为极点,x轴的正半轴为极轴,建立极坐标系,曲线C的极坐标方程为
(1)求直线l的普通方程及曲线C的直角坐标方程;
(2)设直线l与曲线C交于两点,求.
23.(本题满分为10分)求证:
(1);
(2).
中山市第一中学2017-2018学年高二年级第二次统测
理科数学参考答案
【答案】
1. D 2. A 3. A 4. A 5. C 6. A 7. B
8. A 9. D 10. C 11. B 12. B
13. 180 14. 15. 16.
17. 解:设随机选取一件产品,能够通过检测的事件为A,事件A包括两种情况,一是抽到的是一个一等品,二是抽到的是一个二等品,这两种情况是互斥的,
事件“选取一等品都通过检测或者是选取二等品通过检测”;
由题可知X可能取值为.
,
的分布列是:
18. 解:
把代入回归方程得,解得.
回归方程为;
当时,,估计当气温为时的用电量为30度.
19. 解:因为
所以
由此猜想数列的通项公式
下面用数学归纳法证明
当时,,猜想成立
假设当 时,猜想成立,即
那么.
即当时,猜想也成立;
综合可知,对猜想都成立,即
20. 解:第项系数为,第r项系数为,第项系数为依题意得到,即,解得,
所以二项式系数最大的项是第4项和第5项.
所以.
设第项的系数最大,则
解得
又因为,所以
展开式中系数最大的项为
21. 解:,则函数在处的切线的斜率为.
又,
所以函数在处的切线方程为,即
Ⅱ.
当时,在区间上单调递增;
当时,令,解得;
令,解得.
综上所述,当时,函数的增区间是;
当时,函数的增区间是,减区间是.
Ⅲ依题意,函数没有零点,
即无解.
由Ⅱ知,当时,函数在区间上为增函数,区间上为减函数,
由于,只需,
解得.
所以实数a的取值范围为
22. 解:直线l的参数方程为为参数,
消去t得到:,
即:.
曲线C的极坐标方程为
转化为:,
整理得:.
将l的参数方程为参数,代入曲线C:,
整理得:,
所以:,
则:.
23. 证明:,
;
要证,
只要证,
只要证,
只要证,
只要证,
显然成立,
故.