高考文科数学复习：夯基提能作业本 (50) 9页

第七节　抛物线 A组　基础题组 ‎1.以x轴为对称轴,原点为顶点的抛物线上的一点P(1,m)到焦点的距离为3,则抛物线的方程是(　　)‎ A.y=4x2 B.y=8x2‎ C.y2=4x D.y2=8x ‎2.(2016课标全国Ⅱ,5,5分)设F为抛物线C:y2=4x的焦点,曲线y=kx(k>0)与C交于点P,PF⊥x轴,则k=(　　)‎ A.‎1‎‎2‎ B.1 C.‎3‎‎2‎ D.2‎ ‎3.(2016课标全国Ⅰ,10,5分)以抛物线C的顶点为圆心的圆交C于A,B两点,交C的准线于D,E两点.已知|AB|=4‎2‎,|DE|=2‎5‎,则C的焦点到准线的距离为(　　)‎ A.2 B.4 C.6 D.8‎ ‎4.已知抛物线y2=2px(p>0),过其焦点且斜率为-1的直线交抛物线于A,B两点,若线段AB的中点的横坐标为3,则该抛物线的准线方程为(　　)‎ A.x=1 B.x=2 C.x=-1 D.x=-2‎ ‎5.设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则C的方程为(　　)‎ A.y2=4x或y2=8x B.y2=2x或y2=8x C.y2=4x或y2=16x D.y2=2x或y2=16x ‎6.抛物线y2=2px(p>0)上横坐标为6的点到此抛物线焦点的距离为10,则该抛物线的焦点到准线的距离为　　　　. ‎ ‎7.已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4,且位于x轴上方的点,A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M.‎ ‎(1)求抛物线的方程;‎ ‎(2)若过M作MN⊥FA,垂足为N,求点N的坐标.‎ ‎8.已知圆C过定点F‎-‎1‎‎4‎,0‎,且与直线x=‎1‎‎4‎相切,圆心C的轨迹为E,曲线E与直线l:y=k(x+1)(k∈R)相交于A,B两点.‎ ‎(1)求曲线E的方程;‎ ‎(2)当△OAB的面积等于‎10‎时,求k的值.‎ B组　提升题组 ‎9.设F为抛物线y2=2x的焦点,A、B、C为抛物线上三点,若F为△ABC的重心,则|FA|+|FB|+|FC|的值为(　　)‎ A.1 B.2 C.3 D.4‎ ‎10.已知抛物线C:y2=8x的焦点为F,准线为l,P是l上一点,Q是直线PF与C的一个交点.若FP=4FQ,则|QF|=(　　)‎ A.‎7‎‎2‎ B.3 C.‎5‎‎2‎ D.2‎ ‎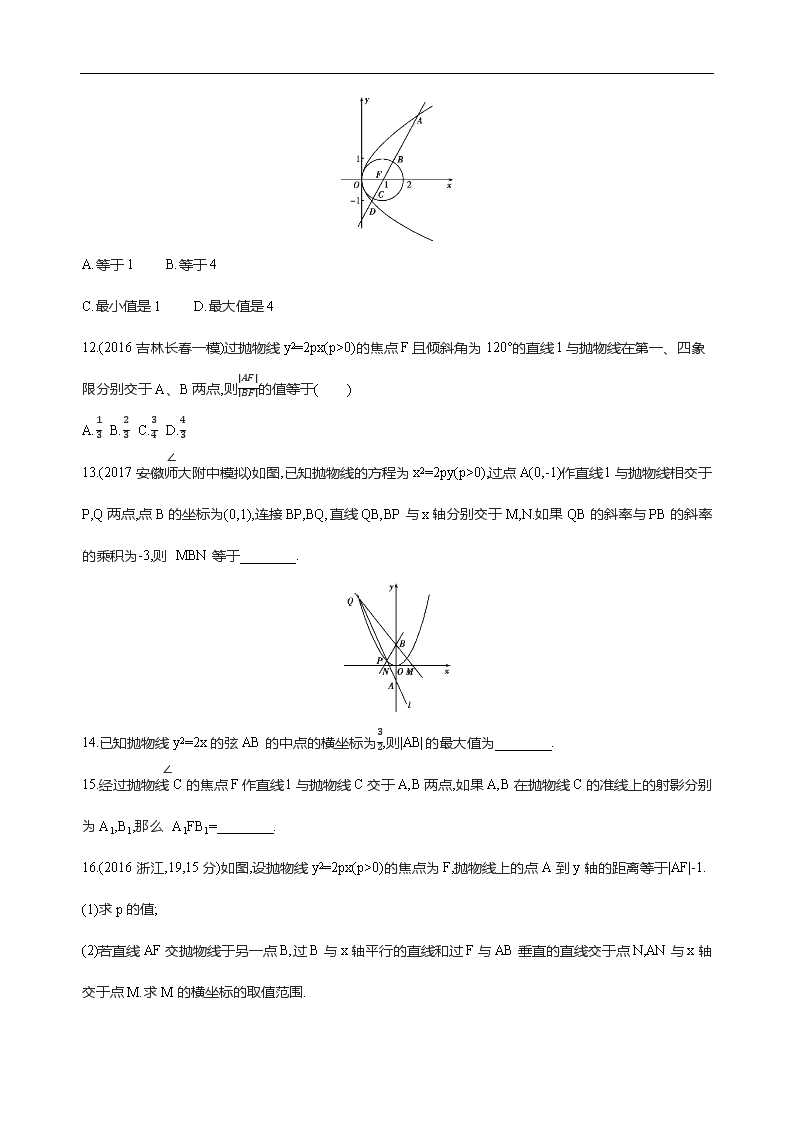11.已知抛物线y2=4x,圆F:(x-1)2+y2=1,过点F作直线l,自上而下顺次与上述两曲线交于点A,B,C,D(如图所示),则下列关于|AB|·|CD|的值的说法中,正确的是(　　)‎ A.等于1 B.等于4‎ C.最小值是1 D.最大值是4‎ ‎12.(2016吉林长春一模)过抛物线y2=2px(p>0)的焦点F且倾斜角为120°的直线l与抛物线在第一、四象限分别交于A、B两点,则‎|AF|‎‎|BF|‎的值等于(　　)‎ A.‎1‎‎3‎ B.‎2‎‎3‎ C.‎3‎‎4‎ D.‎‎4‎‎3‎ ‎13.(2017安徽师大附中模拟)如图,已知抛物线的方程为x2=2py(p>0),过点A(0,-1)作直线l与抛物线相交于P,Q两点,点B的坐标为(0,1),连接BP,BQ,直线QB,BP与x轴分别交于M,N.如果QB的斜率与PB的斜率的乘积为-3,则∠MBN等于　　　　. ‎ ‎14.已知抛物线y2=2x的弦AB的中点的横坐标为‎3‎‎2‎,则|AB|的最大值为　　　　. ‎ ‎15.经过抛物线C的焦点F作直线l与抛物线C交于A,B两点,如果A,B在抛物线C的准线上的射影分别为A1,B1,那么∠A1FB1=　　　　. ‎ ‎16.(2016浙江,19,15分)如图,设抛物线y2=2px(p>0)的焦点为F,抛物线上的点A到y轴的距离等于|AF|-1.‎ ‎(1)求p的值;‎ ‎(2)若直线AF交抛物线于另一点B,过B与x轴平行的直线和过F与AB垂直的直线交于点N,AN与x轴交于点M.求M的横坐标的取值范围.‎ 答案全解全析 A组　基础题组 ‎1.D　设抛物线的方程为y2=2px(p>0),则由抛物线的定义知1+p‎2‎=3,即p=4,所以抛物线方程为y2=8x.‎ ‎2.D　由题意得点P的坐标为(1,2).把点P的坐标代入y=kx(k>0)得k=1×2=2,故选D.‎ ‎3.B　不妨设C:y2=2px(p>0),A(x1,2‎2‎),则x1=‎(2‎‎2‎‎)‎‎2‎‎2p=‎4‎p,由题意可知|OA|=|OD|,得‎4‎p‎2‎+8=p‎2‎‎2‎+5,解得p=4(舍负).故选B.‎ ‎4.C　由题可知焦点为p‎2‎‎,0‎,∴直线AB的方程为y=-x-‎p‎2‎,与抛物线方程联立得y=-x-‎p‎2‎,‎y‎2‎‎=2px,‎消去y得4x2-12px+p2=0,设A(x1,y1),B(x2,y2),则x1+x2=3p.∵线段AB的中点的横坐标为3,∴‎3p‎2‎=3,∴p=2,∴抛物线的准线方程为x=-1.‎ ‎5.C　∵以MF为直径的圆过点(0,2),‎ ‎∴点M在第一象限.‎ 由|MF|=xM+p‎2‎=5可得M5-p‎2‎,‎2p‎5-‎p‎2‎.‎ 从而以MF为直径的圆的圆心N的坐标为‎5‎‎2‎‎,‎‎1‎‎2‎‎2p‎5-‎p‎2‎,‎ ‎∵点N的横坐标恰好等于圆的半径,‎ ‎∴圆与y轴切于点(0,2),‎ 从而2=‎1‎‎2‎‎2p‎5-‎p‎2‎,‎ 即p2-10p+16=0,解得p=2或p=8,‎ ‎∴抛物线方程为y2=4x或y2=16x.故选C.‎ ‎6.答案　8‎ 解析　由题意知,抛物线的准线方程为x=-p‎2‎(p>0),则根据抛物线的性质有p‎2‎+6=10,解得p=8,所以抛物线的焦点到准线的距离为8.‎ ‎7.解析　(1)抛物线y2=2px的准线为x=-p‎2‎,于是4+p‎2‎=5,∴p=2,‎ ‎∴抛物线方程为y2=4x.‎ ‎(2)由(1)知点A的坐标是(4,4),由题意得B(0,4),M(0,2).‎ 又∵F(1,0),∴kFA=‎4‎‎3‎.‎ ‎∵MN⊥FA,∴kMN=-‎3‎‎4‎,‎ ‎∴FA的方程为y=‎4‎‎3‎(x-1),①‎ MN的方程为y=-‎3‎‎4‎x+2,②‎ 由①②联立得x=‎8‎‎5‎,y=‎4‎‎5‎,‎ ‎∴N的坐标为‎8‎‎5‎‎,‎‎4‎‎5‎.‎ ‎8.解析　(1)设圆心C的坐标为(x,y),由题意,知圆心C到定点F‎-‎1‎‎4‎,0‎和直线x=‎1‎‎4‎的距离相等,‎ 故圆心C的轨迹E的方程为y2=-x.‎ ‎(2)由方程组y‎2‎‎=-x,‎y=k(x+1)‎消去x,并整理得ky2+y-k=0.‎ 设A(x1,y1),B(x2,y2),‎ 则y1+y2=-‎1‎k,y1y2=-1.‎ 设直线l与x轴交于点N,则N(-1,0).‎ ‎∴S△OAB=S△OAN+S△OBN=‎1‎‎2‎|ON||y1|+‎1‎‎2‎|ON||y2|=‎1‎‎2‎|ON||y1-y2|=‎1‎‎2‎×1×‎(y‎1‎+y‎2‎‎)‎‎2‎-4‎y‎1‎y‎2‎=‎1‎‎2‎‎1‎k‎2‎‎+4‎.‎ ‎∵S△OAB=‎10‎,∴‎1‎‎2‎‎1‎k‎2‎‎+4‎=‎10‎,‎ 解得k=±‎1‎‎6‎.‎ 经检验,k=±‎1‎‎6‎均符合题意,∴k=±‎1‎‎6‎.‎ ‎ ‎ B组　提升题组 ‎9.C　设点A(x1,y1)、B(x2,y2)、C(x3,y3),又焦点F‎1‎‎2‎‎,0‎,x1+x2+x3=3×‎1‎‎2‎=‎3‎‎2‎,则|FA|+|FB|+|FC|=x‎1‎‎+‎‎1‎‎2‎+x‎2‎‎+‎‎1‎‎2‎+x‎3‎‎+‎‎1‎‎2‎=(x1+x2+x3)+‎3‎‎2‎=‎3‎‎2‎+‎3‎‎2‎=3.‎ ‎10.B　∵FP=4FQ,‎ ‎∴点Q在线段PF上,且在两端点之间,过Q作QM⊥l,垂足为M,‎ 由抛物线定义知|QF|=|QM|,‎ 设抛物线的准线l与x轴的交点为N,‎ 则|FN|=4,又易知△PQM∽△PFN,则‎|QM|‎‎|FN|‎=‎|PQ|‎‎|PF|‎,‎ 即‎|QM|‎‎4‎=‎3‎‎4‎.∴|QM|=3,即|QF|=3.故选B.‎ ‎11.A　设直线l:x=ty+1,代入抛物线方程,得y2-4ty-4=0.设A(x1,y1),D(x2,y2),根据抛物线的定义知,|AF|=x1+1,|DF|=x2+1,故|AB|=x1,|CD|=x2,所以|AB|·|CD|=x1x2=y‎1‎‎2‎‎4‎·y‎2‎‎2‎‎4‎=‎(‎y‎1‎y‎2‎‎)‎‎2‎‎16‎.而y1y2=-4,故|AB|·|CD|=1.‎ ‎12.A　记抛物线y2=2px的准线为l',如图,作AA1⊥l',BB1⊥l',AC⊥BB1,垂足分别是A1,B1,C,则有cos∠ABB1=‎|BC|‎‎|AB|‎=‎|BB‎1‎|-|AA‎1‎|‎‎|AF|+|BF|‎=‎|BF|-|AF|‎‎|AF|+|BF|‎,‎ 即cos 60°=‎|BF|-|AF|‎‎|AF|+|BF|‎=‎1‎‎2‎,因此得‎|AF|‎‎|BF|‎=‎1‎‎3‎.‎ ‎13.答案　‎π‎3‎ 解析　易知直线PQ的斜率存在,设直线PQ的方程为y=kx-1,P(x1,y1),Q(x2,y2),‎ 由y=kx-1,‎x‎2‎‎=2py得x2-2pkx+2p=0,‎ 则x1+x2=2pk,x1x2=2p,‎ kBP=y‎1‎‎-1‎x‎1‎,kBQ=y‎2‎‎-1‎x‎2‎,‎ kBP+kBQ=kx‎1‎-2‎x‎1‎+‎kx‎2‎-2‎x‎2‎ ‎=‎‎2kx‎1‎x‎2‎-2(x‎1‎+x‎2‎)‎x‎1‎x‎2‎ ‎=‎2k·2p-2·2pk‎2p=0,即kBP+kBQ=0,①‎ 又kBP·kBQ=-3,②‎ 联立①②解得kBP=‎3‎,kBQ=-‎3‎,‎ 所以∠BNM=π‎3‎,∠BMN=π‎3‎,‎ 故∠MBN=π-∠BNM-∠BMN=π‎3‎.‎ ‎14.答案　4‎ 解析　设A(x1,y1),B(x2,y2),由题意得x1+x2=3,利用抛物线的定义可知,|AF|+|BF|=x1+x2+1=4,由图可知|AF|+|BF|≥|AB|⇒|AB|≤4,当且仅当直线AB过焦点F时,|AB|取得最大值4.‎ ‎15.答案　‎π‎2‎ 解析　由抛物线定义可知|BF|=|BB1|,|AF|=|AA1|,‎ 故∠BFB1=∠BB1F,∠AFA1=∠AA1F.‎ 又∠OFB1=∠BB1F,∠OFA1=∠AA1F,‎ 故∠BFB1=∠OFB1,∠AFA1=∠OFA1,‎ 又∠AFA1+∠OFA1+∠OFB1+∠BFB1=π,‎ 所以∠OFA1+∠OFB1=‎1‎‎2‎×π=π‎2‎,‎ 即∠A1FB1=π‎2‎.‎ ‎16.解析　(1)由题意可得,抛物线上点A到焦点F的距离等于点A到直线x=-1的距离,由抛物线的定义得p‎2‎=1,即p=2.‎ ‎(2)由(1)得,抛物线方程为y2=4x,F(1,0),可设A(t2,2t),t≠0,t≠±1.‎ 因为AF不垂直于y轴,可设直线AF:x=sy+1(s≠0),由y‎2‎‎=4x,‎x=sy+1‎消去x得y2-4sy-4=0,‎ 故y1y2=-4,所以B‎1‎t‎2‎‎,-‎‎2‎t.‎ 又直线AB的斜率为‎2tt‎2‎‎-1‎,故直线FN的斜率为-t‎2‎‎-1‎‎2t.‎ 从而得直线FN:y=-t‎2‎‎-1‎‎2t(x-1),直线BN:y=-‎2‎t.‎ 所以Nt‎2‎‎+3‎t‎2‎‎-1‎‎,-‎‎2‎t.‎ 设M(m,0),由A,M,N三点共线得 ‎2tt‎2‎‎-m‎=‎2t+‎‎2‎tt‎2‎‎-‎t‎2‎‎+3‎t‎2‎‎-1‎,‎ 于是m=‎2‎t‎2‎t‎2‎‎-1‎.‎ 所以m<0或m>2.‎ 经检验,m<0或m>2满足题意.‎ 综上,点M的横坐标的取值范围是(-∞,0)∪(2,+∞).‎