数学卷·2018届河北省定州中学高二上学期（承智班）周练（10-16）数学试题 （解析版） 16页

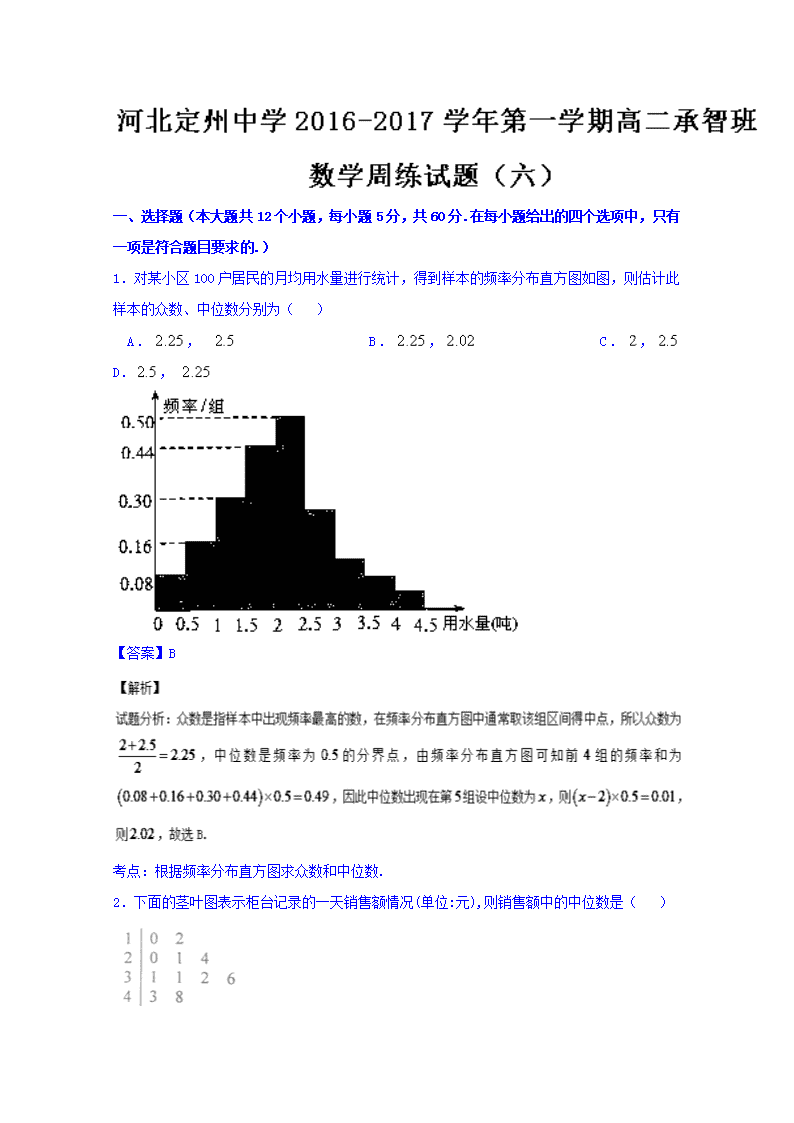
一、选择题（本大题共 12 个小题，每小题 5 分，共 60 分.在每小题给出的四个选项中，只有 一项是符合题目要求的.） 1．对某小区 100 户居民的月均用水量进行统计，得到样本的频率分布直方图如图，则估计此 样本的众数、中位数分别为（ ） A ． ， B ． ， C ． ， D． ， 【答案】B 考点：根据频率分布直方图求众数和中位数. 2．下面的茎叶图表示柜台记录的一天销售额情况(单位:元),则销售额中的中位数是（ ） 2.25 2.5 2.25 2.02 2 2.5 2.5 2.25 A.30.5 B.31 C.31.5 D.32 【答案】B 【解析】 试题分析：由茎叶图可知，样本中共有 个数，所以中位数为由小到大排列后的第 个数， 所以中位数为 ，故选 B. 考点：由茎叶图求中位数. 3．为了了解我校今年准备报考飞行员的学生的体重情况，将所得的数据整理后，画出了频率 分布 直方图(如图)，已知图中从左到右的前 3 个小组的频率之比为 1∶2∶3，第 2 小组的频数为 12，则抽取 的学生总人数是（ ） A.12 B.24 C.48 D.56 【答案】C 考点：频率分布直方图与频数． 4．在样本的频率分布直方图中，共有 n 个小矩形，若中间一个小矩形的面积等于其余(n－1) 个小 矩形面积的 ，且样本容量为 300，则中间一组的频数为（ ） A.30 B.40 C.50 11 6 31 1 5 D.60 【答案】C 【解析】 试题分析：因为中间一个小矩形的面积等于其余 个小矩形面积的 ，所以中间一组的面 积为所有矩形面积和的 ，因此中间一组的频数为 ，故选 C. 考点：频率分布直方图与频数. 5．某校开展“爱我海西、爱我家乡”摄影比赛，9 位评委为参赛作品 A 给出的分数如下图所 示．记 分员在去掉一个最高分和一个最低分后，算得平均分为 91.复核员在复核时，发现有一个数 字(茎叶图中 的 x)无法看清．若记分员计算无误，则数字 x 应该是（ ） A.1 B.2 C.3 D.4 【答案】A 【解析】 试题分析：由题意可知 ，解得 ，所以 ， 故选 A. 考点：茎叶图与平均数． 6．某学校从高三甲、乙两个班中各选 6 名同掌参加数学竞赛，他们取得的成绩（满分 100 分） 的 茎叶图如右图所示，其中甲班学生成绩的众数是 85，乙班学生成绩的平均分为 81，则 x+y 的值为（ ） 1n − 1 5 1 6 1300 506 × = ( )1 89 89 92 93 92 91 917 m+ + + + + + = 91x = 1x = A.6 B. 7 C.8 D.9 【答案】D 考点：茎叶图、众数、平均数． 7．从某小学随机抽取 100 名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图 （如 图）．若要从身高在三组内的学生中，用分层抽样的方法选取 18 人参加一项活动，则从身高在内的学生中选取的人数应为（ ） A ． B ． C ． D． 【答案】B 【解析】 试题分析：由频率分布直方图可知 ， ，所以后 组的频数比为 ，即 ，所以身高在 内 的学生中选取的人数应为 ，故选 B. 考点：分层抽样与频率分布直方图． 8．某商场在国庆黄金周的促销活动中，对 10 月 1 日 9 时至 14 时的销售额进行统计，其频率 分布 直方图如图所示.已知 9 时至 10 时的销售额为 3 万元，则 11 时至 12 时的销售额为（ ） 2 3 4 5 ( )10 1 0.005 0.01 0.02 0.035 10 0.3a× = − + + + × = 0.030a∴ = 3 0.03:0.02:0.01 3: 2:1 [ ]140,150 118 36 × = A. 8 万 元 B. 10 万 元 C. 12 万 元 D. 15 万 【答案】C 考点：由频率分布直方图求频数． 9．甲乙两位歌手在“中国好声音”选拔赛中,5 次得分情况如茎叶图所示,记甲、乙两人的平 均得分 分别为 、 ,则下列判断正确的是（ ） A. ，乙比甲成绩稳定 B. ，甲比乙成绩稳定 C. ，甲比乙成绩稳定 D. ，乙比甲成绩稳定 【答案】A 14 0.20 0.25 0.30 0.35 0.40 0.15 0.10 0 时间 0.05 9 10 11 12 13 频率／组距 x甲 x乙 6 7 7 5 8 8 8 6 8 4 0 9 3 甲 乙 x x<甲 乙 x x<甲 乙 x x>甲 乙 x x>甲 乙 考点：茎叶图、平均数、方差． 【方法点睛】本题主要考查了茎叶图，样本平均数与方差及其数学意义.解题的关键是根据茎 叶图和平均数的公式 ，求出两人的平均数，为方便计算可根据样本数 据特点先都减去 再计算平均数，方差体现了样本数据的稳定程度，方差越小，样本数据越 稳定，根据方差公式求出两组的方差即可两人成绩的稳定性. 10．为监测幼儿身体发育状况，某幼儿园对“大班”的 100 名幼儿的体重做了测量，并根据 所得数 据画出了频率分布直方图，如图所示.则体重在 （单位 kg）的幼儿人数为（ ） A.10 B.15 C.30 D.75 【答案】B 【解析】 试题分析：由频率分布直方图可知体重在 之间的频率为 ，所以频数 为 ，故选 B. 考点：频率与频数. 11．为了了解某校九年级 1600 名学生的体能情况，随机抽查了部分学生，测试 1 分钟仰卧起 坐的 成绩（次数），将数据整理后绘制成如图所示的频率分布直方图，根据统计图的数据，下列 结论错误的是 （ ） [ )18,20 [ )18,20 ( )1 2 1 nx x x xn = + + + 80 0.075 2 0.15× = 100 0.15 15× = A．该校九年级学生 1 分钟仰卧起坐的次数的中位数为 26.25 次 B．该校九年级学生 1 分钟仰卧起坐的次数的众数为 27.5 次 C．该校九年级学生 1 分钟仰卧起坐的次数超过 30 次的人数约有 320 人 D．该校九年级学生 1 分钟仰卧起坐的次数少于 20 次的人数约有 32 人 【答案】D 考点：频率分布直方图、频率、频数、众数、中位数. 【方法点晴】本题主要考查了频率分布直方图、频率、频数、众数、中位数，属于基础题.频 率分布直方图中，中位数是频率为 的横坐标的分界点，众数是指样本中出现频率最高的数， 在频率分布直方图中通常取纵坐标最高的一组区间的中点，某一小组的频数就是该组的频率 （矩形面积）乘以样本容量，把握好这些技巧即可顺利完成由频率分布直方图对样本的分析. 12．某企业开展职工技能比赛，并从参赛职工中选 1 人参加该行业全国技能大赛.经过 6 轮选 拔， 甲、乙两人成绩突出，得分情况如茎叶图所示. 若甲乙两人的平均成绩分别是 ， ，则下列说法正确的是（ ） （A） ，乙比甲成绩稳定，应该选乙参加比赛 （B） ，甲比乙成绩稳定，应该选甲参加比赛 0.5 x甲 x乙 x x>甲 乙 x x>甲 乙 （C） ，甲比乙成绩稳定，应该选甲参加比赛 （D） ，乙比甲成绩稳定，应该选乙参加比赛 【答案】D 考点：茎叶图、平均数、方差的数学意义. 【方法点睛】本题主要考查了茎叶图，样本平均数与方差及其数学意义.解题的关键是根据茎 叶图和平均数的公式 ，求出两人的平均数，为方便计算可根据样本数 据特点先都减去 再计算平均数，方差体现了样本数据的稳定程度，方差越小，样本数据越 稳定，根据方差公式求出两组的方差即可两人成绩的稳定性. 第Ⅱ卷（非选择题共 90 分） 二、填空题（本大题共 4 小题，每题 5 分，满分 20 分．） 13．从高三年级随机抽取 100 名学生，将他们的某次考试数学成绩绘制成频率分布直方图．由 图中 数据可知成绩在的人数分别为 6 人和 3 人 所以抽取的 3 人中分数在的人有 （人） 8 分 （3）由（2）知：抽取的 3 人中分数在的人有 1 人，记为 ，从中随机抽取 2 人 总的情形有 三种． 而分数在各 1 人的情形有 两种 故所求概率 12 分 考点：频率分布直方图、分层抽样与古典概型中某事件的概率. 19．城市公交车的数量若太多则容易造成资源的浪费；若太少又难以满足乘客需求.某市公交 公司 在某站台的 60 名候车乘客中随机抽取 15 人，将他们的候车时间作为样本分成 5 组，如下 表所示（单位： 分钟）： x x<甲 乙 x x<甲 乙 ( )1 2 1 nx x x xn = + + + 80 33 19 × = c ( , ),( , ),( , )a b a c b c ( , ),( , )a c b c 2 3P = 组别 候车时间 人数 一 2 二 6 三 4 四 2 五 1 （1）估计这 60 名乘客中候车时间少于 10 分钟的人数； （2）若从上表第三、四组的 6 人中任选 2 人作进一步的调查，求抽到的两人恰好来自不同 组的概率． 【答案】（1） ；（2） ． （2）将第三组乘客编号为 ，第四组乘客编号为 ．从 人中任选两人有包含 以下基本事件： ， ， ， ， 共 个基本事件， 10 分 其中两人恰好来自不同组包含 个基本事件，所以所求概率为 ． 12 分 考点：样本频率与总体频率、古典概型中某事件的概率. 20．对某电子元件进行寿命追踪调查，所得样本数据的频率分布直方图如下. [0,5) [5,10) [10,15) [15,20) [20,25] 32 8 15 1 2 3 4, , ,a a a a 1 2,b b 6 1 2 1 3 1 4 1 1 1 2( , ),( , ),( , ),( , ),( , )a a a a a a a b a b 2 3 2 4 2 1 2 2( , ),( , ),( , ),( , )a a a a a b a b 3 4 3 1 3 2( , ),( , ),( , )a a a b a b 4 1 4 2( , ),( , )a b a b 1 2( , )b b 15 8 8 15 （1）求 ，并根据图中的数据，用分层抽样的方法抽取 个元件，元件寿命落在 之间 的应抽取几个？ （2）从（1）中抽出的寿命落在 之间的元件中任取 个元件，求事件“恰好有一 个元件寿命落 在 之间，一个元件寿命落在 之间”的概率. 【答案】（1） ， ；（2） ． 【解析】 试题分析：（1）由各矩形面积和为 ，求出第二组的面积即频率，根据矩形面积公式可求得 ，根据前两组的频率可得其在总体中所占比例，乘以样本容量可得寿命落在 之 间的元件个数；（2）记“寿命落在 之间的 个元件”，分别 ，“落在 之间的 个元件有”，分别记为： ，从中任取 个元件，列举出所有的基本事件，找出 满足条件的基本事件，即可求得概率. （2）记“恰好有一个寿命落在 之间，一个寿命为 之间”为事件 ，易 知，寿命落在 之间的元件有 个，分别记 ，落在 之间的元件有 个，分别记为： ，从中任取 个元件，有如下基本事件： ， ，共有 个基本事件. 9 分 事件 “恰好有一个寿命落在 之间，一个寿命为 之间”有： 0y 20 100 ~ 300 100 ~ 300 2 0 0.0015y = 5 3 5 0y 100 ~ 300 100 ~ 200 2 1 2,a a 200 ~ 300 3 1 2 3, ,b b b 2 100 ~ 200 200 ~ 300 A 100 ~ 200 2 1 2,a a 200 ~ 300 3 1 2 3, ,b b b 2 ( ) ( ) ( ) ( )1 2 1 1 1 2 1 3, , , , , , ,a a a b a b a b ( ) ( ) ( )2 1 2 2 2 3, , , , ,a b a b a b ( ) ( ) ( )1 2 1 3 2 3, , , , ,b b b b b b 10 A 100 ~ 200 200 ~ 300 100 ~ 200 200 ~ 300 1 ， ，共有 个基本事件 10 分 ∴ 11 分 ∴事件“恰好有一个寿命落在 之间，一个寿命为 之间”的概率为 12 分 考点：频率分布直方图与古典概型． 21．某班主任对全班 50 名学生进行了作业量多少的调查．数据如下表： 认为作业多 认为作业不多 合计 喜欢玩游戏 18 9 不喜欢玩游戏 8 15 合计 （1）请完善上表中所缺的有关数据； （2）试通过计算说明在犯错误的概率不超过多少的前提下认为喜欢玩游戏与作业量的多少 有关系？ 附： P(K2≥K0) 0.05 0.025 0.010 0.005 0.001 K0 3.841 5.024 6.635 7.879 10.828 【答案】（1）列联表见解析；（2）在犯错误的概率不超过 的前提下认为喜欢玩游戏与 作业量的多少有关系． 试题解析：(1) 认为作业多 认为作业不多 合计 喜欢玩游戏 18 9 27 不喜欢玩游戏 8 15 23 合计 26 24 50 ( ) ( ) ( )1 1 1 2 1 3, , , , ,a b a b a b ( ) ( ) ( )2 1 2 2 2 3, , , , ,a b a b a b 6 6 3( ) 10 5P A∴ = = 100 ~ 200 200 ~ 300 3 5 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d −= + + + + 0.025 (2) 将 表 中 的 数 据 代 入 公 式 得 到 的 观 测 值 ≈ 5.059>5.024， 查表知 P(K2≥5.024)＝0.025，即说明在犯错误的概率不超过 0.025 的前提下认为喜欢玩游戏 与作业量的多少有关系． 考点： 列联表与相关性检验． 22．某校高一（1）班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损， 可 见部分如下图． （1）求分数在 的频率及全班人数； （2）求分数在 之间的频数，并计算频率分布直方图中 间矩形的高； （3）若要从分数在 之间的试卷中任取两份分析学生失分情况，求在抽取的试卷中， 至少有一份 分数在 之间的概率． 【答案】（1） ， ；（2） ， ；（3） ． 分数 频率 组距 0.044 0.028 0.012 0.008 10090807060500 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d −= + + + + 2K 2 2× [50 60)， [80 90)， [80 90)， [80 100)， [90 100)， 0.08 25 3 0.012 0.7 （2）分数在 之间的频数为 ； 频率分布直方图中 间的矩形的高为 .7 分 （3）将 之间的 个分数编号为 , 之间的 个分数编号为 ， 8 分 在 之 间 的 试 卷 中 任 取 两 份 的 基 本 事 件 为 ： 共 个， 10 分 其中，至少有一个在 之间的基本事件有 个， 故至少有一份分数在 之间的概率是 . 13 分 考点：频率分布直方图与茎叶图、古典概型中某事件的概率. 23．随机抽取某中学高一级学生的一次数学统测成绩得到一样本，其分组区间和频数是： ， 2； ，7； ，10； ，x；，2.其频率分布直方图受到破坏，可见部分如 下 图所示，据此解答如下问题. [ )60,50 [ )70,60 [ )80,70 [ )90,80 [ )80,90 25 22 3− = [ )80,90 3 10 0.01225 ÷ = [ )80,90 3 1 2 3a a a， ， [ )90,100 2 1 2b b， [ )80,100 1 2 1 3 1 1 1 2 2 3( ) ( ) ( ) ( ) ( )a a a a a b a b a a， ， ， ， ， ， ， ， ， ， 2 1 2 2 3 1 3 2 1 2( ) ( ) ( ) ( ) ( )a b a b a b a b b b， ， ， ， ， ， ， ， ， 10 [ )90,100 7 [ )90,100 7 0.710 = （1）求样本的人数及 x 的值； （2）估计样本的众数，并计算频率分布直方图中 的矩形的高； （3）从成绩不低于 80 分的样本中随机选取 2 人，该 2 人中成绩在 90 分以上（含 90 分）的 人数记为 ， 求 的数学期望. 【答案】(1) ， ；(2) ；(3) ． 试题解析：（1）由题意得，分数在 之间的频数为 2，频率为 ，（1 分） 所以样本人数为 （人） （2 分） 的值为 （人）. （4 分） （2）从分组区间和频数可知，样本众数的估计值为 . （6 分） 由（1）知分数在 之间的频数为 4，频率为 （7 分） 所以频率分布直方图中 的矩形的高为 （8 分） （3）成绩不低于 80 分的样本人数为 4+2=6（人），成绩在 90 分以上(含 90 分)的人数为 人， [80,90) ξ ξ 4x = 2 3 [50,60) 0.008 10 0.08× = 2 250.08n = = x 25 (2 7 10 2) 4x = − + + + = 75 [80,90) 4 0.1625 = [80,90) 0.16 0.01610 = 2 25 75,0.016 所以 的取值为 0，1，2. （9 分） ， ， ，（10 分） 所以 的分布列为： 0 1 2 （11 分） 所以 的数学期望为 （13 分） 考点：频率分布直方图、众数、频率与频数及离散型随机变量的分布列. 【方法点晴】本题主要考查了频率分布直方图、众数、频率与频数及离散型随机变量的分布 列等，属于基础题.本题解答时从 组的频率和频数入手求出样本容量，即可求得 组的频数，结合该组的频率求出矩形的高，求离散性随机变量的分布列首先找出其可 能的取值，结合其取每个值对应的意义求出概率，数学期望就容易解答了. 24．为了比较两种治疗失眠症的药(分别称为 A 药，B 药)的疗效，随机地选取 20 位患者服用 A 药， 20 位患者服用 B 药，这 40 位患者在服用一段时间后，记录他们日平均增加的睡眠时间(单 位：h)．试验 的观测结果如下： 服用 A 药的 20 位患者日平均增加的睡眠时间： 0.6 1.2 2.7 1.5 2.8 1.8 2.2 2.3 3.2 3.5 2.5 2.6 1.2 2.7 1.5 2.9 3.0 3.1 2.3 2.4 服用 B 药的 20 位患者日平均增加的睡眠时间： 3.2 1.7 1.9 0.8 0.9 2.4 1.2 2.6 1.3 1.4 1.6 0.5 1.8 0.6 2.1 1.1 2.5 1.2 2.7 0.5 (1) 分别计算两组数据的平均数，从计算结果看，哪种药的疗效更好？ (2) 根据两组数据完成下面茎叶图，从茎叶图看，哪种药的疗效更好？ ξ  15 6)0( 2 6 2 4 === C CP ξ 1 1 4 2 2 6 8( 1) 15 C CP C ξ = = = 2 2 2 6 1( 2) 15 CP C ξ = = = ξ ξ ( )P ξ 6 15 8 15 1 15 ξ 6 8 1 20 1 215 15 15 3Eξ = × + × + × = [50,60) [80,90) A 药 B 药 0. 1. 2. 3. 【答案】（1） 药的疗效更好；（2） 药的疗效更好． 【解析】 试题分析：（1）根据样本数据平均数的公式分别求出两组的平均数，即可比较它们的疗效； （2）完成茎叶图，根据两组数据的集中位置即可判断它们的疗效差别. (2) 由观测结果可绘制如下茎叶图： 从以上茎叶图可以看出，A 药疗效的试验结果有 的叶集中在茎 2、3 上，而 B 药疗效的试验 结果有 的叶集中在茎 0、1 上，由此可看出 A 药的疗效更好． 考点：样本平均数与茎叶图. 【方法点晴】本题主要考查了样本平均数与茎叶图，根据样本的数字特征和茎叶图估计整体， 属于基础题.本题中，求样本平均数时，因数据众多容易计算错误，可分别求出所有小数的和 的平均数，来简化计算；用茎叶图估计样本数据分布情况时，主要看数据集中的区域取值水 平，相对数字特征，茎叶图更直观，在要求不太高的情况下，比平均数更方便. A A 7 10 7 10