2019年高考数学高分突破复习课件考前冲刺三 第三类 13页

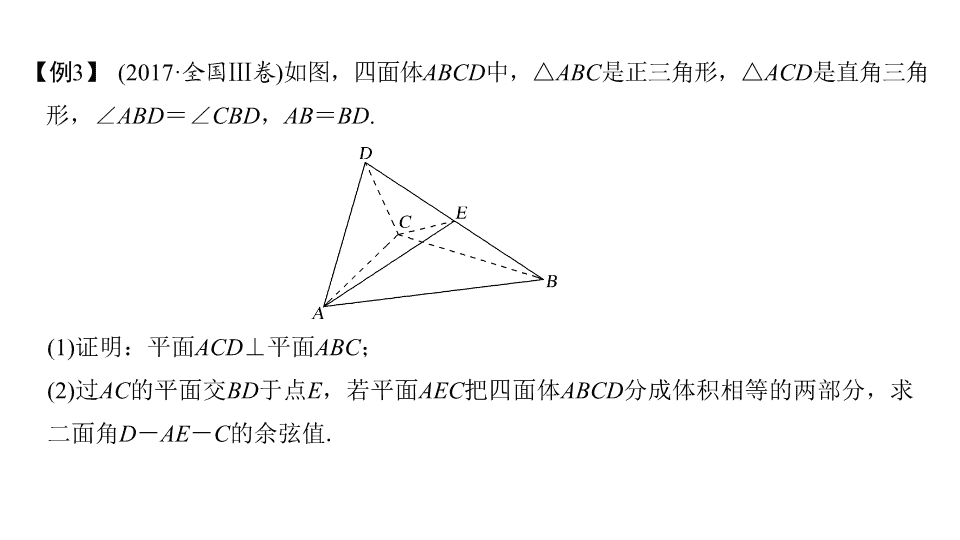
第三类　立体几何问题重在 “ 建 ” —— 建模、建系 立体几何解答题的基本模式是论证推理与计算相结合，以某个几何体为依托，分步设问，逐层加深，解决这类题目的原则是建模、建系 . 建模 —— 将问题转化为平行模型、垂直模型及平面化模型；建系 —— 依托于题中的垂直条件，建立空间直角坐标系，利用空间向量求解 . 【例 3 】 (2017· 全国 Ⅲ 卷 ) 如图，四面体 ABCD 中， △ ABC 是正三角形， △ ACD 是直角三角形， ∠ ABD ＝ ∠ CBD ， AB ＝ BD . (1) 证明：平面 ACD ⊥ 平面 ABC ； (2) 过 AC 的平面交 BD 于点 E ，若平面 AEC 把四面体 ABCD 分成体积相等的两部分，求二面角 D － AE － C 的余弦值 . (1) 证明 　由题设可得， △ ABD ≌△ CBD . 从而 AD ＝ DC ，又 △ ACD 为直角三角形， 所以 ∠ ADC ＝ 90° ， 取 AC 的中点 O ，连接 DO ， BO ，则 DO ⊥ AC ， DO ＝ AO ， 又由于 △ ABC 是正三角形，故 BO ⊥ AC ， 所以 ∠ DOB 为二面角 D － AC － B 的平面角 . ( 建模 ) 在 Rt △ AOB 中， BO 2 ＋ OA 2 ＝ AB 2 ， 又 AB ＝ BD ，所以 BO 2 ＋ DO 2 ＝ BO 2 ＋ AO 2 ＝ AB 2 ＝ BD 2 ，故 ∠ DOB ＝ 90° ， 所以 平面 ACD ⊥ 平面 ABC . (2) 解 　由题设及 (1) 知， OA ， OB ， OD 两两垂直，以 O 为坐标原点， 设平面 AED 的一个法向量为 n 1 ＝ ( x 1 ， y 1 ， z 1 ) ，平面 AEC 的一个法向量为 n 2 ＝ ( x 2 ， y 2 ， z 2 ) ， 探究提高 　 1.(1) 建模：构建二面角的平面角模型 . (2) 建系：以两两垂直的直线为坐标轴 . 2 . 破解策略：立体几何的内容在高考中的考查情况总体上比较稳定，因此，复习备考时往往有 “ 纲 ” 可循，有 “ 题 ” 可依 . 在平时的学习中，要加强 “ 一题两法 ( 几何法与向量法 ) ” 的训练，切勿顾此失彼；要重视识图训练，能正确确定关键点或线的位置，将局部空间问题转化为平面问题；能依托于题中的垂直条件，建立适当的空间直角坐标系，将几何问题化归为代数问题 . 【训练 3 】 ( 2018· 日照一模 ) 如图所示的几何体 ABCDE 中， DA ⊥ 平面 EAB ， CB ∥ DA ， EA ＝ DA ＝ AB ＝ 2 CB ， EA ⊥ AB ， M 是线段 EC 上的点 ( 不与端点重合 ) ， F 为线段 DA 上的点， N 为线段 BE 的中点 . (1) 证明　 如图 1 ，连接 MN ，因 M ， N 分别是线段 EC ，线段 BE 的中点， 又 CB ∥ DA ， ∴ MN ∥ DA ， ∴ MN ∥ FD . 所以四边形 MNFD 为平行四边形， ∴ FN ∥ MD . 又 FN  平面 MBD ， MD  平面 MBD ，所以 FN ∥ 平面 MBD . 图 1 (2) 解　 由已知，分别以 AE ， AB ， AD 所在直线为 x 轴、 y 轴、 z 轴建立空间直角坐标系 A － xyz ，如图 2 ，设 CB ＝ 1 ，则 A (0 ， 0 ， 0) ， B (0 ， 2 ， 0) ， C (0 ， 2 ， 1) ， D (0 ， 0 ， 2) ， E (2 ， 0 ， 0) ， 图 2 由已知，平面 ABD 的一个法向量为 n 1 ＝ (1 ， 0 ， 0) ， 设平面 MBD 的法向量为 n ＝ ( x ， y ， z ) ， 解之得， λ ＝ 1 或 λ ＝ 3. 又因为平面 ABD 与平面 MBD 所成二面角为锐角， 所以 λ ＝ 1.