- 353.50 KB
- 2024-03-26 发布
绝密★启用前
磐安县第二中学高二数学10月月考试卷卷
考试时间:120分钟;总分:150分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、 选择题:本大题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。
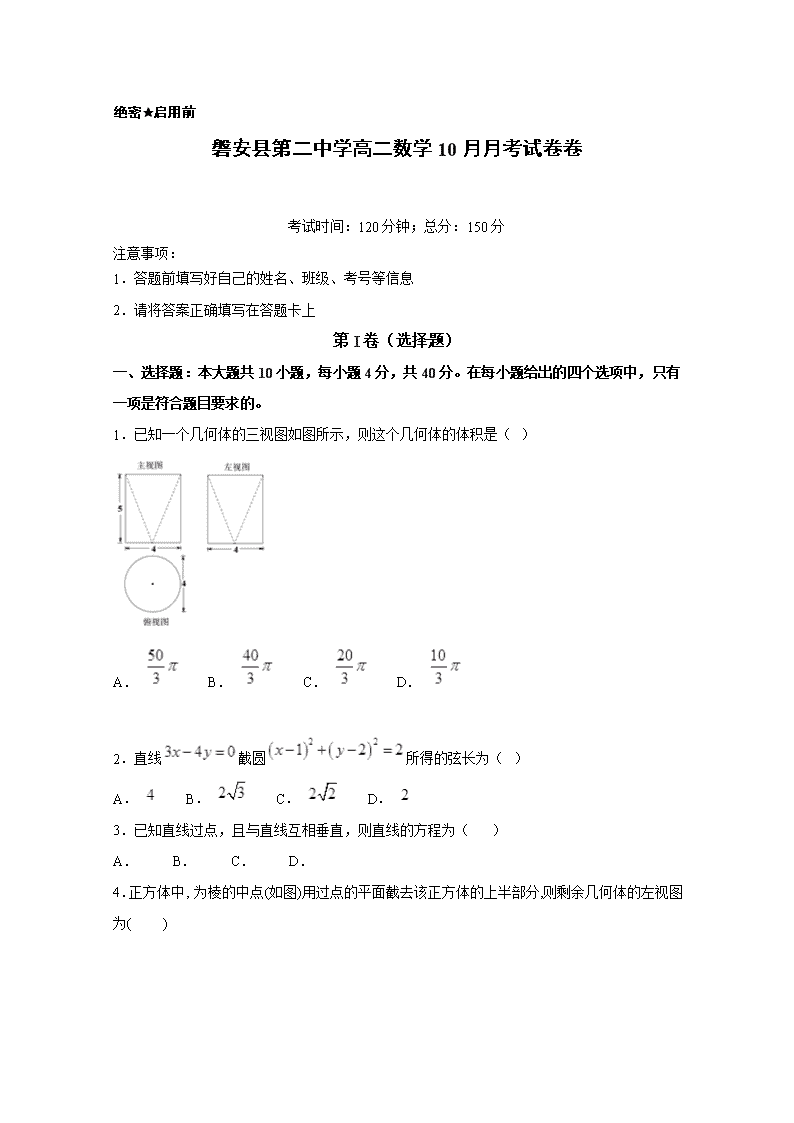
1.已知一个几何体的三视图如图所示,则这个几何体的体积是( )
A. B. C. D.
2.直线截圆所得的弦长为( )
A. B. C. D.
3.已知直线过点,且与直线互相垂直,则直线的方程为( )
A. B. C. D.
4.正方体中, 为棱的中点(如图)用过点的平面截去该正方体的上半部分,则剩余几何体的左视图为( )
A. B.
C. D.
5.下列命题中,正确的是( ).
①若一平面内有两条直线都与另一平面平行,则这两个平面平行;
②若一平面内有无数条直线与另一平面平行,则这两个平面平行;
③若一平面内任何一条直线都平行于另一平面,则这两个平面平行;
④若一平面内的两条相交直线分别与另一平面平行,则这两个平面平行.
A. ①③ B. ②④ C. ③④ D. ②③④
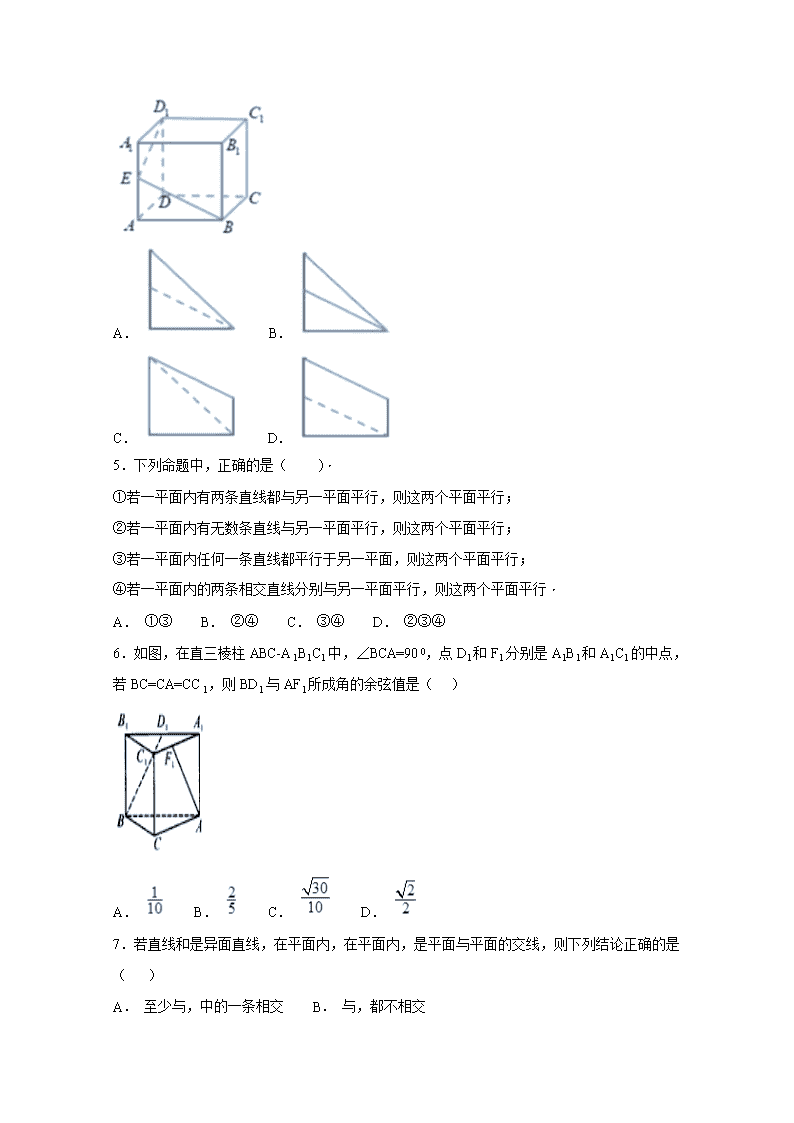
6.如图,在直三棱柱ABC-A1B1C1中,∠BCA=900,点D1和F1分别是A1B1和A1C1的中点,若BC=CA=CC1,则BD1与AF1所成角的余弦值是( )
A. B. C. D.
7.若直线和是异面直线,在平面内,在平面内,是平面与平面的交线,则下列结论正确的是( )
A. 至少与,中的一条相交 B. 与,都不相交
C. 与,都相交 D. 至多与,中的一条相交
8.如图,在正方体中,分别是的中点,则下列命题正确的是( )
A. B. C. 平面 D. 平面
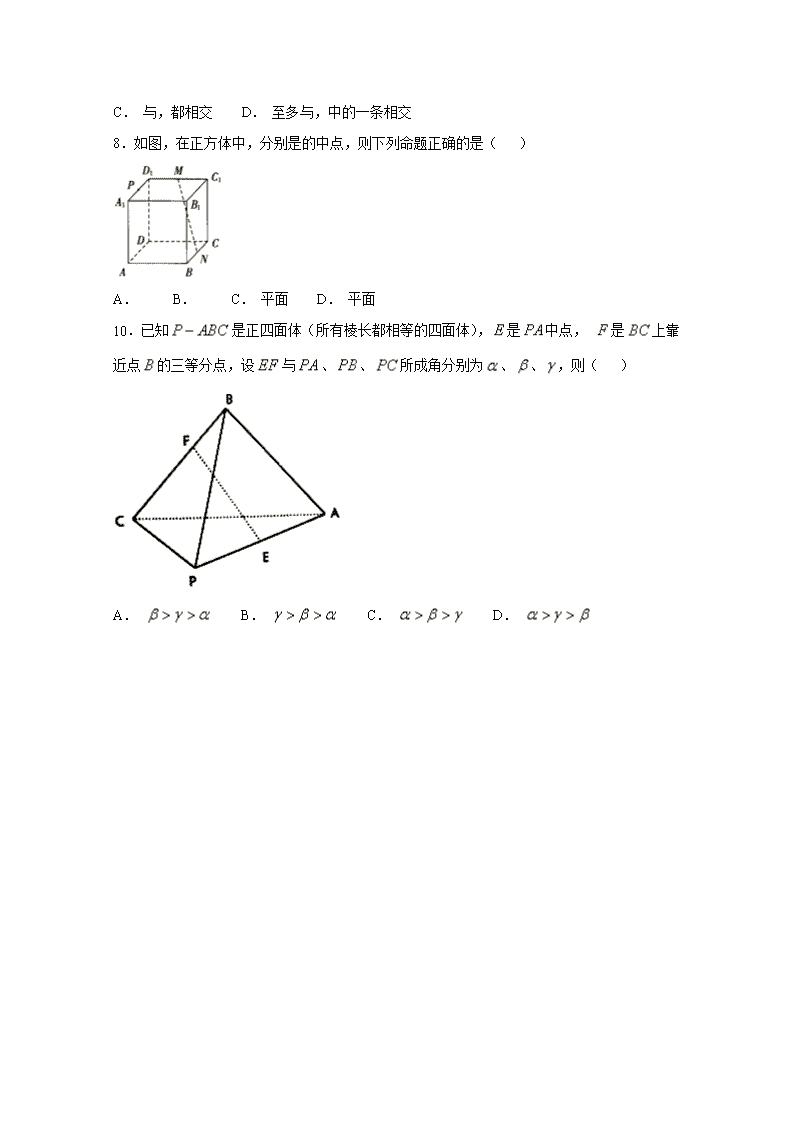
10.已知是正四面体(所有棱长都相等的四面体),是中点, 是上靠近点的三等分点,设与、、所成角分别为、、,则( )
A. B. C. D.
第II卷(非选择题)
二、填空题:本大题共7个小题,多空题每小题6分,单空题每小题4分,共36分。
11.已知直线与直线互相垂直,则=_______;若互相平行,则=_______。
12.一个棱长为2的正方体被一个平面截去一部分后,剩下部分的三视图如下图所示,则该几何体的表面积为____________,体积为_________.
13.在平面直角坐标系中,为坐标原点,点,动点满足,则点轨迹方程为_________________________;若动点在圆上,则的取值范围为______________ .
14.如图,棱长为2的正方体中,M是棱AA1的中点,过C,M,D1作正方体的截面,则截面的面积是________.
15.一个正方体纸盒展开后如图所示,在原正方体纸盒中有如下结论
①AB⊥EF;
②AB与CM所成的角为60°;
③EF与MN是异面直线;
④MN∥CD.
以上四个命题中,正确命题的序号是 _________
16.如图,在三棱柱中,底面,,,是的中点,则直线与所成角的余弦值为__________.直线与所成角的余弦值为__________
17.在下列四个命题中,正确的命题的有__________________.
①已知直线ax+by+c-1=0(bc>0)经过圆x2+y2-2y-5=0的圆心,则的最小值是10;
②若圆上有且只有两个点到直线的距离为1,则 ;
③若实数满足的取值范围为 ;
④点M在圆上运动,点为定点,则|MN|的最大值是7.
三.解答题:本大题共5小题。满分74分。解答应写出文字说明,证明过程和演算步骤。
18.如图所示,正方体ABCD-A1B1C1D1中,E、F分别是AB和AA1的中点.
求证:(1)E、C、D1、F四点共面;
(2) CE、D1F、DA三线共点.
19.如图,四边形是平行四边形,点, , 分别为线段, , 的中点.
()证明平面;
()证明平面平面;
()在线段上找一点,使得平面,并说明理由
20.如图,四棱锥的底面是边长为1的正方形,侧棱底面,且, 是侧棱上的动点.
(Ⅰ)求四棱锥的体积;
(Ⅱ)如果是的中点,求证平面;
(Ⅲ)是否不论点在侧棱的任何位置,都有?证明你的结论.
21.已知直线l:
1证明直线l经过定点并求此点的坐标;
2若直线l不经过第四象限,求k的取值范围;
3若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设的面积为S,求S的最小值及此时直线l的方程.
22.已知关于的方程.
(Ⅰ)若方程表示圆,求的取值范围;
(Ⅱ)若圆与圆外切,求的值;
(Ⅲ)若圆与直线相交于两点,且,求的值.