2014年高考试题——数学理（北京卷）解析版 11页

2014 年北京高考数学（理科）试题解析 一、选择题 1. [2014•北京理卷] 1.已知集合 2{ | 2 0}, {0,1,2}A x x x B    ，则 AB ( ) .{0}A .{0,1}B .{0,2}C .{0,1,2}D 【答案】C 【解析】∵  }2,0A ，∴      2,02,1,02,0   BA . 2.[2014•北京理卷] 下列函数中，在区间(0, ) 上为增函数的是（ ） .1A y x 2. ( 1)B y x .2xCy  0.5. log ( 1)D y x 【答案】A 【解析】由初等函数的性质得选项 B 在 1,0 上递减，选项 C、D 在 ,0 为减函数，所以 排除 B、C、D. 3.[2014•北京理卷] 曲线 1 cos 2 sin x y        （ 为参数）的对称中心（ ） .A 在直线 2yx 上 .B 在直线 2yx 上 .C 在直线 1yx上 .D 在直线 1yx上 【答案】B 【解析】曲线方程消参化为    121 22  yx ，其对称中心为  2,1 ，验证知其满足 xy 2 . 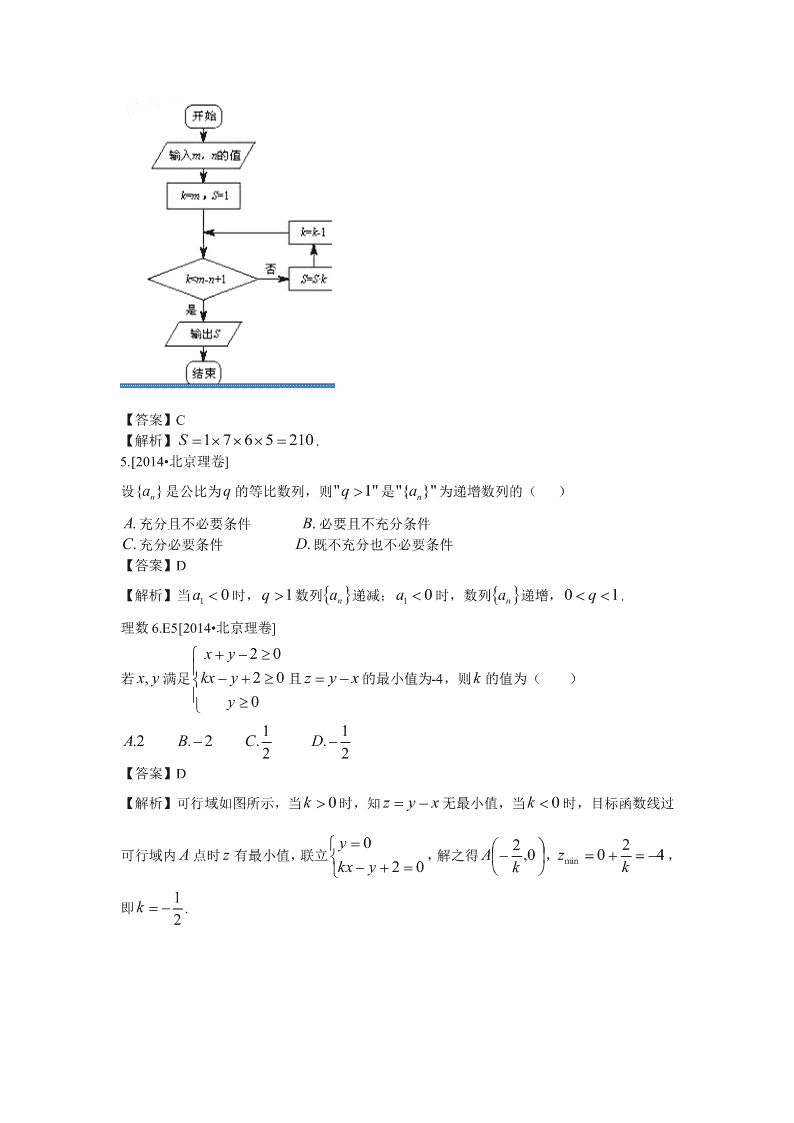4.[2014•北京理卷] 当 7, 3mn时，执行如图所示的程序框图，输出的 S 值为（ ） .7A .42B .210C .840D 【答案】C 【解析】 2105671 S . 5.[2014•北京理卷] 设{}na 是公比为 q 的等比数列，则" 1"q  是"{ }"na 为递增数列的（ ） .A 充分且不必要条件 .B 必要且不充分条件 .C 充分必要条件 .D 既不充分也不必要条件 【答案】D 【解析】当 01 a 时， 1q 数列 na 递减； 时，数列 na 递增， 10  q . 理数 6.E5[2014•北京理卷] 若 ,xy满足 20 20 0 xy kx y y          且 z y x的最小值为-4，则 k 的值为（ ） .2A .2B  1.2C 1. 2D 【答案】D 【解析】可行域如图所示，当 0k 时，知 xyz  无最小值，当 0k 时，目标函数线过 可行域内 A 点时 z 有最小值，联立      02 0 ykx y ，解之得    0,2 kA ， 420min  kz ， 即 2 1k . 7.[2014•北京理卷] 在空间直角坐标系Oxyz 中，已知  2,0,0A ，  2,2,0B ，  0,2,0C ，  1,1, 2D ，若 1S ， 2S ， 3S 分别表示三棱锥 D ABC 在 xOy ， yOz ， zOx 坐标平面上的正投影图形的 面积，则（ ） （A） 1 2 3S S S （B） 12SS 且 31SS （C） 13SS 且 32SS （D） 23SS 且 13SS 【答案】D 【解析】设顶点 D 在三个坐标面 xoy 、 yoz 、 zox 的正投影分为  1D 、  2D 、  3D ，则 211  BDAD ， 2AB ，∴ 22222 1 1 S ， 2222 1 2 2  OCD SS ， 2222 1 3 3  OAD SS . 8.[2014•北京理卷] 有语文、数学两学科，成绩评定为“优秀”“合格”“不合格”三种.若 A 同学每科成绩不 低于 B 同学，且至少有一科成绩比 高，则称“ 同学比 同学成绩好.”现有若干同学， 他们之间没有一个人比另一个成绩好，且没有任意两个人语文成绩一样，数学成绩也一样 的.问满足条件的最多有多少学生（ ） （A） 2 （B）3 （C） 4 （D）5 【答案】B 【解析】假设 AB 两个同学的数学成绩一样，由题意知他们语文成绩不一样，这样他们的语 文成绩总有人比另一个人高，语文成绩较高的同学比另一个同学“成绩好”，与已知条件“他 们之中没有一个比另一个成绩好”相矛盾.因此，没有任意两个同学数学成绩是相同的.因为数 学成绩只有 3 种，因而同学数量最大为 3.即 3 位同学成绩分别为（优秀，不合格）、（合格， 合格）、（不合格，优秀）时满足条件. 二、填空题 9.[2014•北京理卷] 02  yx 02  ykx A 0 xy 复数 21 1 i i  ________. 【答案】 1 【解析】      12 2 11 1 1 1 2222               i ii i i i . 10.[2014•北京理卷] 已知向量 a 、b 满足 1a  ，  2,1b  ，且  0a b R   ，则   ________. 【答案】 5 【解析】∵ 0 ba ，∴ ba  ，∴ 51 5 || ||||  a b . 11.[2014•北京理卷] 设双曲线C 经过点 2,2 ，且与 2 2 14 y x具有相同渐近线，则 的方程为________； 渐近线方程为________. 【答案】 1123 22  yx ； xy 2 【解析】设双曲线C 的方程为  2 2 4 xy ，将 2,2 代入  324 2 2 2 ，∴双曲线方 程为 .令 04 2 2  xy 得渐近线方程为 . 12.[2014•北京理卷] 若等差数列 na 满足 7 8 9 0a a a   ， 7 10 0aa，则当 n  ________时 的前 n 项和最大. 【答案】8 【解析】∵ 03 8987  aaaa ， 098107  aaaa ，∴ 0,0 98  aa ，∴ 8n 时 数列 na 前 n 和最大. 13.[2014•北京理卷] 把 5 件不同产品摆成一排，若产品 A 与产品 B 相邻，且产品 A 与产品 C 不相邻，则不同的 摆法有 种 【答案】36 【解析】 363261 3 2 2 3 3 AAA . 14.[2014•北京理卷] 设函数 )sin()(   xxf ， 0,0  A ，若 )(xf 在区间 ]2,6[  上具有单调性，且              63 2 2  fff ，则 )(xf 的最小正周期为________. 【答案】 【解析】结合图象得 2 62 2 3 2 2 4     T ，即 T . 15.[2014•北京理卷] 如图，在 ABC 中， 8,3  ABB  ，点 D 在 BC 边上，且 7 1cos,2  ADCCD （1）求 BADsin （2）求 ACBD, 的长 解：（I）在 ADC 中，因为 1 7COS ADC，所以 43sin 7ADC. 所以sin sin( )BAD ADC B    sin cos cos sinADC B ADC B    = 14 33 2 3 7 1 2 1 7 34  . （Ⅱ）在 ABD 中，由正弦定理得 A A 6  2  3 2 338sin 14 3sin 43 7 AB BADBD ADB    ， 在 ABC 中，由余弦定理得 2 2 2 2 cosAC AB BC AB BC B     22 18 5 2 8 5 492       , 所以 7AC  . 16.[2014•北京理卷] 李明在 10 场篮球比赛中的投篮情况如下（假设各场比赛互相独立）： （1）从上述比赛中随机选择一场，求李明在该场比赛中投篮命中率超过 6.0 的概率. （2）从上述比赛中选择一个主场和一个客场，求李明的投篮命中率一场超过 6.0 ，一 场不超过 的概率. （3）记 x 是表中 10 个命中次数的平均数，从上述比赛中随机选择一场，记 X 为李明 在这比赛中的命中次数，比较 )(XE 与 的大小（只需写出结论）. 解：(I)根据投篮统计数据，在 10 场比赛中，李明投篮命中率超过 0.6 的场次有 5 场，分别 是主场 2，主场 3，主场 5，客场 2，客场 4. 所以在随机选择的一场比赛中，李明的投篮命中率超过 0.6 的概率是 05. （Ⅱ）设事件 A 为“在随机选择的一场主场比赛中李明的投篮命中率超过 0.6”， 事件 B 为“在随机选择的一场客场比赛中李明的投篮命中率超过 0.6”， 事件 C 为“在随机选择的一个主场和一个客场中，李明的投篮命中率一场超过 0.6， 一场不超过 0.6”。 则 C= AB AB ，A,B 独立。 根据投篮统计数据， 32( ) , ( )55P A P B. ( ) ( ) ( )P C P AB P AB 3 3 2 2 5 5 5 5    13 25 ， 所以，在随机选择的一个主场和一个客场中，李明的投篮命中率一场超过 0.6，一场不超过 0.6 的概率为 13 25 . （Ⅲ） EX x . 17.[2014•北京理卷] 如图，正方形 AMDE 的边长为 2， CB, 分别为 MDAM , 的中点，在五棱锥 ABCDEP 中， F 为棱 PE 的中点，平面 ABF 与棱 PCPD, 分别交于点 HG, . （1）求证： FGAB // ； （2）若 PA 底面 ABCDE ，且 PEAF  ，求直线 BC 与平面 ABF 所成角的大小，并 求线段 PH 的长. 解：（I）在正方形中，因为 B 是 AM 的中点，所以 AB ∥ DE 。 又因为 AB  平面 PDE， 所以 ∥平面 PDE， 因为  平面 ABF，且平面 ABF 平面 PDF FG ， 所以 ∥ FG . （Ⅱ）因为 PA 底面 ABCDE,所以 PA AB ， PA AE . 如图建立空间直角坐标系 Axyz ，则 (0,0,0)A ， (1,0,0)B , (2,1,0)C , (0,0,2)P , (0,1,1)F , BC (1,1,0) . 设平面 ABF 的法向量为 ( , , )n x y z ，则 0, 0, n AB n AF    即 0, 0. x yz    令 1,z  ，则 1y 。所以 (0, 1,1)n ， 设 直 线 BC 与 平 面 ABF 所 成 角 为 a,则 1sin cos , 2 n BCa n BC n BC    . 因此直线 BC 与平面 ABF 所成角的大小为 6 π . 设点 H 的坐标为( , , ).u v w 因为点 H 在棱 PC 上，所以可设 (0 1),PH PC 即 ( , , 2) (2,1, 2).u v w    。所以 2 , , 2 2u v w      . 因为 n 是平面 ABF 的法向量，所以 0n AB，即(0, 1,1) (2 , ,2 2 ) 0      。 解得 2 3  ，所以点 H 的坐标为 422( , , ).333 所以 2 2 24 2 4( ) ( ) ( ) 23 3 3PH      . 18.[2014•北京理卷] 已知函数 ( ) cos sin , [0, ]2f x x x x x    ， （1）求证： ( ) 0fx ； （2）若 sin xabx在(0, )2  上恒成立，求 a 的最大值与b 的最小值. 解：（I）由 ( ) cos sinf x x x x得 '( ) cos sin cos sinf x x x x x x x     。 因为在区间 (0, )2  上 '( )fx sin 0xx ，所以 ()fx在区间 0, 2   上单调递 减。 从而 (0) 0f。 （Ⅱ）当 0x 时，“ sin x ax ”等价于“sin 0x ax ”“ sin x bx ”等价于“sin 0x bx ”。 令 ()gx sin x cx，则 '( )gx cosxc， 当 0c  时， ( ) 0gx 对任意 (0, )2x  恒成立。 当 1c  时，因为对任意 ， 0，所以 在区间 0, 2   上单调递减。从而 (0) 0g  对任意 恒成立。 当01c 时，存在唯一的 0 (0, )2x  使得 0'( )gx 0cos xc0 。 与 在区间(0, )2  上的情况如下： x 0(0, )x 0x 0( , )2x  → 0 → ()gx ↗ ↘ 因为 在区间 00, x 上是增函数，所以 0( ) (0) 0g x g  。进一步，“ ( ) 0gx 对 任意 恒成立”当且仅当 ( ) 1 022gc   ，即 20 c  ， 综上所述，当且仅当 2c  时， ( ) 0gx 对任意 恒成立；当且仅当 时， ( ) 0gx 对任意 恒成立. 所以，若 sin xabx 对任意 恒成立，则 a 最大值为 2  ，b 的最小值为 1. 19. [2014•北京理卷] 已知椭圆 22:24C x y， （1）求椭圆C 的离心率. （2）设O 为原点，若点 A在椭圆 上，点 B 在直线 2y  上，且OA OB ，求直线 AB 与圆 222xy的位置关系，并证明你的结论. 解：（I）由题意，椭圆 C 的标准方程为 22 142 xy。 所以 224, 2ab，从而 2 2 2 2c a b   。因此 2, 2ac。 故椭圆 C 的离心率 2 2 ce a 。 （Ⅱ） 直线 AB 与圆 222xy相切。证明如下： 设点 A,B 的坐标分别为 00( , )xy， ( ,2)t ，其中 0 0x  。 因为OA OB ，所以 0OA OB，即 0020tx y，解得 0 0 2yt x 。 当 0xt 时， 2 0 2 ty  ，代入椭圆 C 的方程，得 2t  ， 故直线 AB 的方程为 2x  。圆心 O 到直线 AB 的距离 2d  。 此时直线 AB 与圆 相切。 当 0xt 时，直线 AB 的方程为 0 0 22 ( )yy x txt    ， 即 0 0 0 0( 2) ( ) 2 0y x x t y x ty      ， 圆心 0 到直线 AB 的距离 00 22 00 2 ( 2) ( ) x tyd y x t     ，又 22 0024xy， 0 0 2yt x 故 2 0 0 0 2 22 0 00 2 0 22 4 4 yx xd yxy x      0 0 42 00 2 0 4 2 8 16 2 x x xx x    此时直线 AB 与圆 相切. 20. [2014•北京理卷] 对于数对序列 1 1 2 2( , ),( , ), ,( , )nnP a b a b a b ，记 1 1 1()T P a b， 1 1 2( ) max{ ( ), }(2 )k k k kT P b T P a a a k n       ，其中 1 1 2max{ ( ), }kkT P a a a    表示 1()kTP 和 12 ka a a   两个数中最大的数， （1）对于数对序列 (2,5), (4,1)PP，求 12( ), ( )T P T P 的值. （2）记 m 为 , , ,a b c d 四个数中最小值，对于由两个数对 ( , ),( , )a b c d 组成的数对序列 ( , ),( , )P a b c d 和 '( , ),( , )P a b c d ，试分别对 ma 和 md 的两种情况比较 2 ()TP和 2 ( ')TP的大小. （3）在由 5 个数对(11,8),(5,2),(16,11),(11,11),(4,6)组成的所有数对序列中，写出一个 数对序列 P 使 5 ()TP最小，并写出 的值.（只需写出结论）. 解：（I） 1( ) 2 5 7TP    11( ) 1 max ( ),2 4T P T P    1 max 7,6 =8 （Ⅱ） 2 ()TP  max ,a b d a c d     2 ( ')TP  max ,c d b c a b    . 当 m=a 时， 2 ( ')TP= = c d b 因为c d b c b d     ，且 a c d c b d     ，所以 ≤ 2 ( ')TP 当 m=d 时，  max ,c d b c a b     c a b   因为 a b d ≤ c a b，且 a c d c a b     所以 ≤ 。 所以无论 m=a 还是 m=d， ≤ 都成立。 （Ⅲ）数对序列 :P （4,6），（11,11），（16,11），（11,8），（ 5,2）的 5 ()TP值最小， 1()TP=10， 2 ()TP=26， 3()TP=42， 4 ()TP=50， =52