- 399.00 KB
- 2024-03-19 发布
高二数学文科试卷
评卷人
得分
一、单项选择(每小题5分,共60分)
1、下列说法中正确的是( )
A.有两个面平行,其余各面都是三角形的几何体叫棱柱
B.有两个面平行,其余各面都是梯形的几何体叫棱台
C.有一个面是多边形,其余各面都是五边形的几何体叫棱锥
D.棱台各侧棱的延长线交于一点
2、将一个等腰梯形绕着它的较长的底边所在直线旋转一周,所得的几何体包括( )
A.一个圆台、两个圆锥 B.两个圆台、一个圆柱
C.两个圆台、一个圆锥 D.一个圆柱、两个圆锥
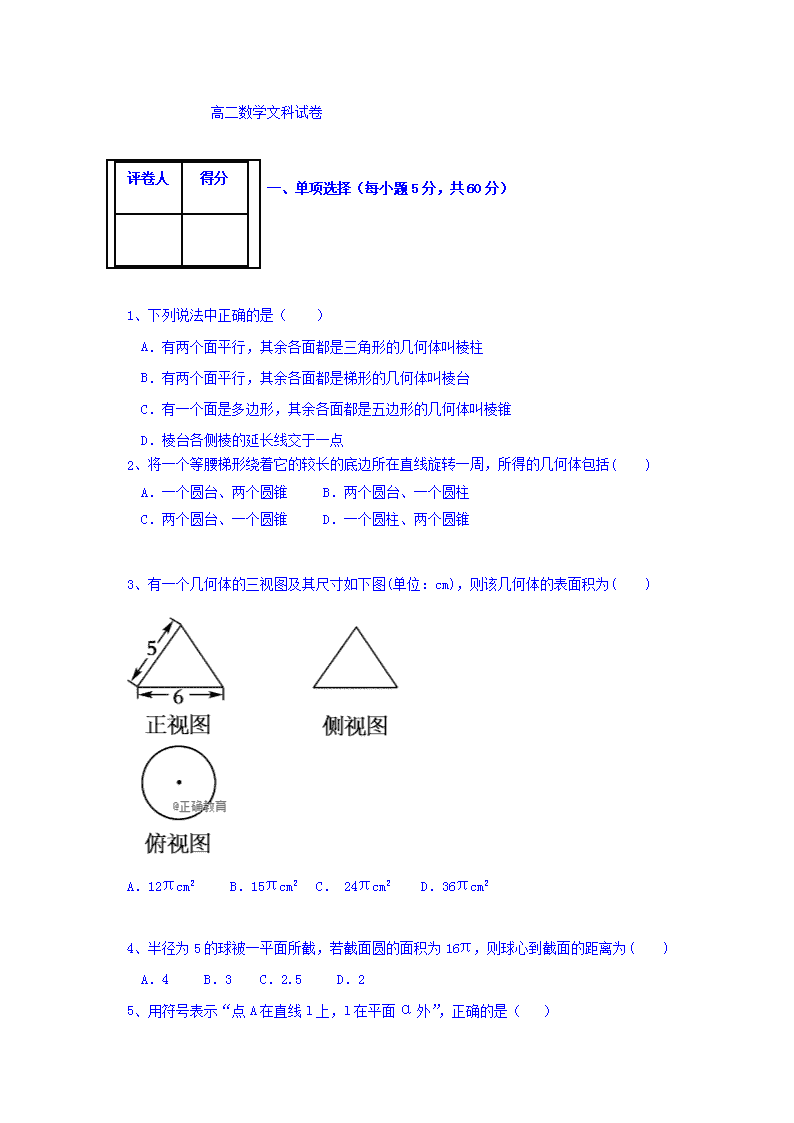
3、有一个几何体的三视图及其尺寸如下图(单位:cm),则该几何体的表面积为( )
A.12πcm2 B.15πcm2 C. 24πcm2 D.36πcm2
4、半径为5的球被一平面所截,若截面圆的面积为16π,则球心到截面的距离为( )
A.4 B.3 C.2.5 D.2
5、用符号表示“点A在直线l上,l在平面α外”,正确的是( )
A. B. C. D.
6、已知直线//平面,直线平面,则( ).
A.// B.与异面 C.与相交 D.与无公共点
7、如图,是水平放置的的直观图,则的面积为
A. 6 B. C. 12 D.
8、长方体的一个顶点上三条棱长分别是,且它的个顶点都在同一球面上,则这个球的表面积是( )
A. B. C. D.都不对
9、已知是两条不同的直线,是两个不同的平面,则下列命题正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
10.空间四边形的两条对角线互相垂直,顺次连接四边中点的四边形一定是( )
A.空间四边形 B.矩形 C.菱形 D.正方形
11、点分别是正方体的棱和的中点,则和所成角的大小为( )
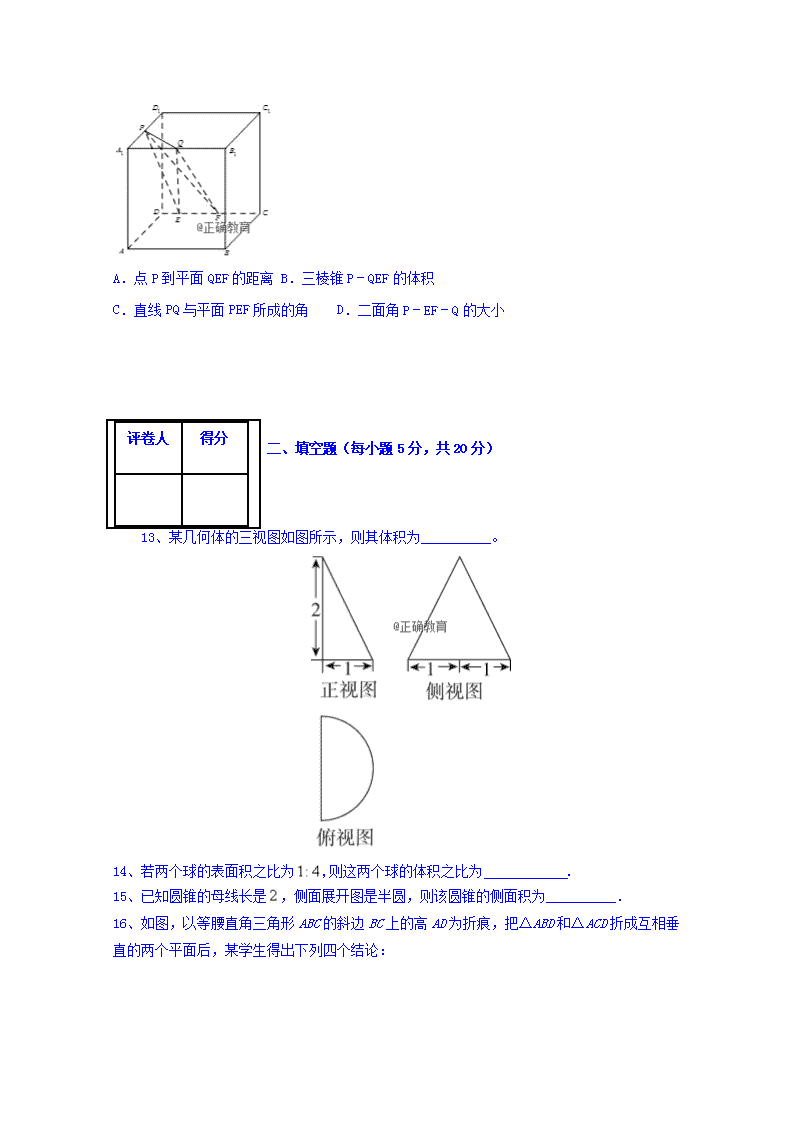
A. B. C. D.
12、如图,在棱长为a的正方体ABCD﹣A1B1C1D1中,P为A1D1的中点,Q为A1B1上任意一点,E,F为CD上任意两点,且EF的长为定值b,则下面的四个值中不为定值的是( )
A.点P到平面QEF的距离 B.三棱锥P﹣QEF的体积
C.直线PQ与平面PEF所成的角 D.二面角P﹣EF﹣Q的大小
评卷人
得分
二、填空题(每小题5分,共20分)
13、某几何体的三视图如图所示,则其体积为__________。
14、若两个球的表面积之比为,则这两个球的体积之比为 .
15、已知圆锥的母线长是,侧面展开图是半圆,则该圆锥的侧面积为__________.
16、如图,以等腰直角三角形ABC的斜边BC上的高AD为折痕,把△ABD和△ACD折成互相垂直的两个平面后,某学生得出下列四个结论:
①BD⊥AC; ②△BAC是等边三角形;
③三棱锥D-ABC是正三棱锥; ④平面ADC⊥平面ABC。
其中正确的是___________
评卷人
得分
三、解答题(每题10分)
17、(12分)如图1,在四棱锥P-ABCD中,底面为正方形,PC与底面ABCD垂直,图2为该四棱锥的正视图和侧视图,它们是腰长为6 cm的全等的等腰直角三角形.
(1) 根据图2所给的正视图、侧视图,画出相应的俯视图,并求出该俯视图的面积;
(2)求侧棱PA的长.
18、(10分)球的两个平行截面的面积分别是5π,8π,两截面间的距离为1,求球的半径.
19、(12分)已知圆锥的正视图是边长为2的正三角形,O是底面圆心.
(Ⅰ)求圆锥的侧面积;
(Ⅱ)经过圆锥的高AO的中点O¢作平行于圆锥底面的截面,求截得的两部分几何体的体积比.
C
11
11
A
D
B
20、(12分)如图,已知在直三棱柱中(侧棱垂直于底面),,,,点是的中点.
求证:;求证:平面.
21、(12分)如图,在四棱锥中,底面是直角梯形,,,,平面,为中点.
(Ⅰ)证明:平面;(Ⅱ)设,,,求点到平面的距离.
22.(12分)如图,在三棱柱中,平面,为正三角形,,为的中点.
(Ⅰ)求证:平面平面;(Ⅱ)求三棱锥的体积.
高二数学文科试卷答案
一. 选择题
1--5 DDCBB 6--10 DCBBB 11--12 BC
二. 填空题
13. 14. 15. 16.①②③
三、解答题
17、解(1)该四棱锥的俯视图为内含对角线,边长为6 cm的正方形,如图,其面积为36 cm2.
(2)由侧视图可求得
由正视图可知AD=6且AD⊥PD,
所以在Rt△APD中,
18、解。设两个平行截面圆的半径分别为r1,r2,球半径为R,则由πr=5π,得r1=.由πr=8π,得r2=2.
(1)如图所示,当两个截面位于球心O的同侧时,有-=1,所以=1+,解得R=3.
(2) 当两个截面位于球心O的异侧时,有+=1.此方程无解.
所以球的半径是3
19、解:(Ⅰ)由题意得∴
(Ⅱ)设圆锥的高为h,则h=,r=1,
∴小圆锥的高h¢=,小圆锥的底面半径r¢=,
∴
∴.∴
20.解:证明:(1)在中,∵,,,
∴为直角三角形,∴ …………2分
又∵平面,∴, …………3分
, ∴平面,…………5分 (没有相交扣1分)
,∴. …………6分(没有线在面上扣1分)
(2)设与交于点,则为的中点, 连结, ……8分
∵D为AB的中点,∴在△中,,…………10分
又, ……12分 ,……11分
∴平面. ……12分
21.解:(I)作中点,连结、,∴且.
∵且,∴,.
∴四边形是平行四边形.∴.
∵平面,平面,∴平面.
(II)作的中点,连结、.
∵,∴.
又∵,∴四边形是正方形.
∴.
∴中,.
∵,.∴.
∵平面,平面,∴,.
∴平面.∴.
设点到平面的距离为,∴.
∴.∴.
22、解:(Ⅰ)证明:因为底面,所以
因为底面正三角形,是的中点,所以
因为,所以平面
因为平面平面,所以平面平面
(Ⅱ)由(Ⅰ)知中,,
所以
所以