- 697.00 KB
- 2024-03-19 发布
全*品*高*考*网, 用后离不了!2016-2017学年江西省抚州市临川十中高二(上)期中数学试卷(理科)
一、选择题(本大题共12小题,共60分)
1.已知命题P:“∀x∈R,x2+2x+3≥0”,则命题P的否定为( )
A.∀x∈R,x2+2x+3<0 B.∃x∈R,x2+2x+3≥0
C.∃x∈R,x2+2x+3<0 D.∃x∈R,x2+2x+3≤0
2.设抛物线y2=2px的焦点在直线2x+3y﹣8=0上,则该抛物线的准线方程为( )
A.x=﹣4 B.x=﹣3 C.x=﹣2 D.x=﹣1
3.与向量=(12,5)平行的单位向量为( )
A. B.
C.或 D.或
4.对于直线m、n和平面α,下面命题中的真命题是( )
A.如果m⊂α,n⊄α,m、n是异面直线,那么n∥α
B.如果m⊂α,n与α相交,那么m、n是异面直线
C.如果m⊂α,n∥α,m、n共面,那么m∥n
D.如果m∥α,n∥α,m、n共面,那么m∥n
5.下列各命题中正确的是( )
①若命题“p或q”为真命题,则命题“p”和命题“q”均为真命题;
②命题“∃x∈R,x2+1>3x”的否定是“∀x∈R,x2+1≤3x”;
③“x=4”是“x2﹣3x﹣4=0”的充分不必要条件;
④命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0且n≠0”.
A.②③ B.①②③ C.①②④ D.③④
6.如图,AB是平面a的斜线段,A为斜足,若点P在平面a内运动,使得△ABP的面积为定值,则动点P的轨迹是( )
A.圆 B.椭圆 C.一条直线 D.两条平行直线
7.已知二面角α﹣AB﹣β是直二面角,P为棱AB上一点,PQ、PR分别在平面α、β内,且∠QPB=∠RPB=45°,则∠QPR为( )
A.45° B.60° C.120° D.150°
8.设抛物线y2=4x的焦点为F,过点F的直线与抛物线交于A,B两点,过AB的中点M作准线的垂线与抛物线交于点P,若,则弦长|AB|等于( )
A.2 B.4 C.6 D.8
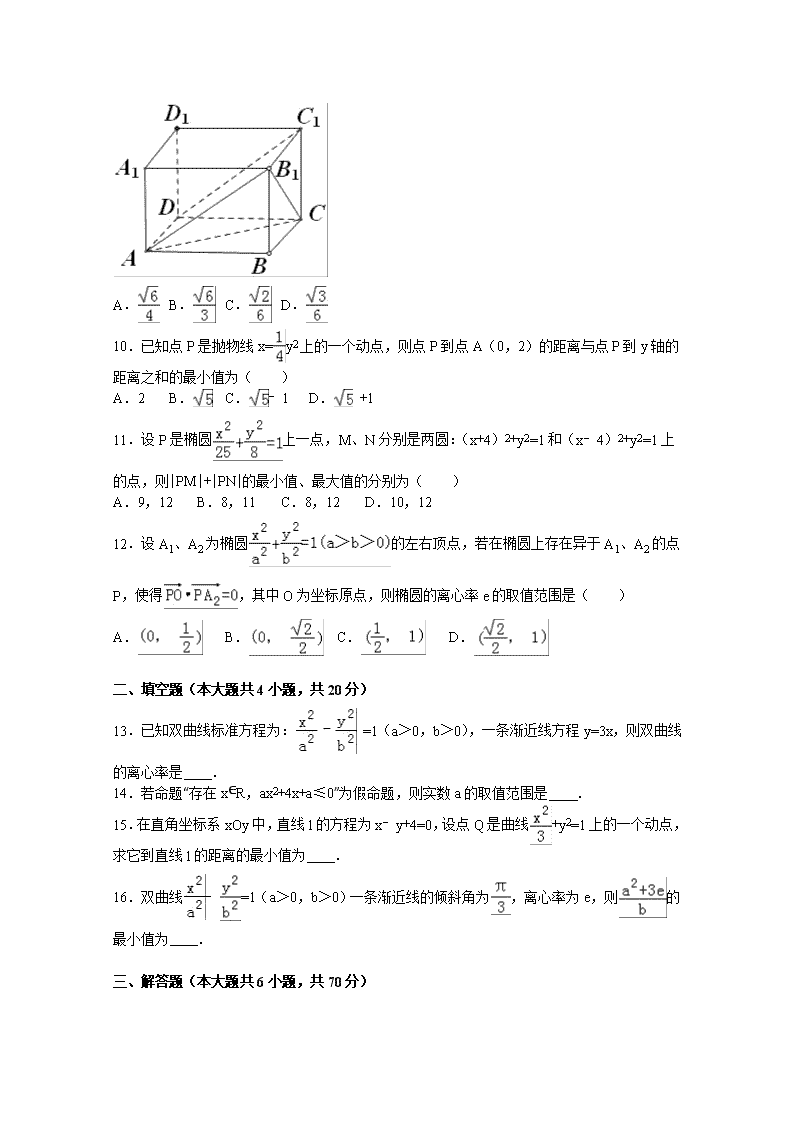
9.在长方体ABCD﹣A1B1C1D1中,B1 C和C1D与底面A1B1C1D1所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )
A. B. C. D.
10.已知点P是抛物线x=y2上的一个动点,则点P到点A(0,2)的距离与点P到y轴的距离之和的最小值为( )
A.2 B. C.﹣1 D. +1
11.设P是椭圆上一点,M、N分别是两圆:(x+4)2+y2=1和(x﹣4)2+y2=1上的点,则|PM|+|PN|的最小值、最大值的分别为( )
A.9,12 B.8,11 C.8,12 D.10,12
12.设A1、A2为椭圆的左右顶点,若在椭圆上存在异于A1、A2的点P,使得,其中O为坐标原点,则椭圆的离心率e的取值范围是( )
A. B. C. D.
二、填空题(本大题共4小题,共20分)
13.已知双曲线标准方程为: =1(a>0,b>0),一条渐近线方程y=3x,则双曲线的离心率是 .
14.若命题“存在x∈R,ax2+4x+a≤0”为假命题,则实数a的取值范围是 .
15.在直角坐标系xOy中,直线l的方程为x﹣y+4=0,设点Q是曲线+y2=1上的一个动点,求它到直线l的距离的最小值为 .
16.双曲线﹣=1(a>0,b>0)一条渐近线的倾斜角为,离心率为e,则的最小值为 .
三、解答题(本大题共6小题,共70分)
17.已知条件p:≤﹣1,条件q:x2+x<a2﹣a,且p是q的一个必要不充分条件,求实数a的取值范围.
18.已知函数
(1)若m=1,求函数f(x)的定义域.
(2)若函数f(x)的值域为R,求实数m的取值范围.
(3)若函数f(x)在区间上是增函数,求实数m的取值范围.
19.已知椭圆C: +=1(a>b>0)的焦距为2,长轴长为4.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)如图,过坐标原点O作两条互相垂直的射线,与椭圆C交于A,B两点.设A(x1,y1),B(x2,y2),直线AB的方程为y=﹣2x+m(m>0),试求m的值.
20.已知向量与.
(Ⅰ)若在方向上的投影为,求λ的值;
(Ⅱ)命题P:向量与的夹角为锐角;
命题q:,其中向量, =()(λ,α∈R).若“p或q”为真命题,“p且q”为假命题,求λ的取值范围.
21.如图,四棱锥S一ABCD中,已知AD∥BC,∠ADC=90°,∠BAD=135°,AD=DC=,SA=SC=SD=2.
(I)求证:AC⊥SD;
(Ⅱ)求二面角A﹣SB﹣C的余弦值.
22.已知圆C1的圆心在坐标原点O,且恰好与直线l1:x﹣2y+3=0相切,点A为圆上一动点,AM⊥x轴于点M,且动点N满足,设动点N的轨迹为曲线C.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l与椭圆C相交于不同两点A,B,且满足(O为坐标原点),求线段AB长度的取值范围.
2016-2017学年江西省抚州市临川十中高二(上)期中数学试卷(理科)
参考答案与试题解析
一、选择题(本大题共12小题,共60分)
1.已知命题P:“∀x∈R,x2+2x+3≥0”,则命题P的否定为( )
A.∀x∈R,x2+2x+3<0 B.∃x∈R,x2+2x+3≥0
C.∃x∈R,x2+2x+3<0 D.∃x∈R,x2+2x+3≤0
【考点】命题的否定.
【分析】据命题否定的规则,对命题“∀x∈R,x2+2x+3≥0”进行否定,注意任意对应的否定词为存在;
【解答】解:根据全称命题的否定是特称命题可知:∀x∈R,x2+2x+3≥0的否定为∃x∈R,x2+2x+3<0
故选C
2.设抛物线y2=2px的焦点在直线2x+3y﹣8=0上,则该抛物线的准线方程为( )
A.x=﹣4 B.x=﹣3 C.x=﹣2 D.x=﹣1
【考点】抛物线的简单性质.
【分析】求出直线与x轴的交点坐标,即抛物线的焦点坐标,从而得出准线方程.
【解答】解:把y=0代入2x+3y﹣8=0得:2x﹣8=0,解得x=4,
∴抛物线的焦点坐标为(4,0),
∴抛物线的准线方程为x=﹣4.
故选:A.
3.与向量=(12,5)平行的单位向量为( )
A. B.
C.或 D.或
【考点】用向量证明平行.
【分析】设出与向量=(12,5)平行的单位向量,求出的模,利用,求出.
【解答】解:设与向量=(12,5)平行的单位向量,
所以
=,或
故选C.
4.对于直线m、n和平面α,下面命题中的真命题是( )
A.如果m⊂α,n⊄α,m、n是异面直线,那么n∥α
B.如果m⊂α,n与α相交,那么m、n是异面直线
C.如果m⊂α,n∥α,m、n共面,那么m∥n
D.如果m∥α,n∥α,m、n共面,那么m∥n
【考点】命题的真假判断与应用.
【分析】由线面的位置关系,即可判断A;由空间直线与直线的位置关系,即可判断B;
运用线面平行的性质定理,即可判断C;由线面平行的性质和直线与直线的位置关系,即可判断D.
【解答】解:对于A.如果m⊂α,n⊄α,m、n是异面直线,则n∥α或n与α相交,故A错;
对于B.如果m⊂α,n与α相交,则m,n是相交或异面直线,故B错;
对于C.如果m⊂α,n∥α,m、n共面,由线面平行的性质定理,可得m∥n,故C对;
对于D.如果m∥α,n∥α,m,n共面,则m∥n或m,n相交,故D错.
故选C.
5.下列各命题中正确的是( )
①若命题“p或q”为真命题,则命题“p”和命题“q”均为真命题;
②命题“∃x∈R,x2+1>3x”的否定是“∀x∈R,x2+1≤3x”;
③“x=4”是“x2﹣3x﹣4=0”的充分不必要条件;
④命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0且n≠0”.
A.②③ B.①②③ C.①②④ D.③④
【考点】命题的真假判断与应用.
【分析】①根据复合命题真假关系进行判断,
②根据特称命题的否定是全称命题进行判断,
③根据充分条件和必要条件的定义进行判断,
④根据否命题的定义进行判断.
【解答】解:①若命题“p或q”为真命题,则命题“p”和命题“q”至少有一个为真命题;故①错误,
②命题“∃x∈R,x2+1>3x”的否定是“∀x∈R,x2+1≤3x”;故②正确,
③由x2﹣3x﹣4=0得x=4或x=﹣1,
则“x=4”是“x2﹣3x﹣4=0”的充分不必要条件;故③正确,
④命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0”故④错误,
故正确的是②③,
故选:A
6.如图,AB是平面a的斜线段,A为斜足,若点P在平面a内运动,使得△ABP的面积为定值,则动点P的轨迹是( )
A.圆 B.椭圆 C.一条直线 D.两条平行直线
【考点】椭圆的定义;平面与圆柱面的截线.
【分析】根据题意,因为三角形面积为定值,从而可得P到直线AB的距离为定值,分析可得,点P的轨迹为一以AB为轴线的圆柱面,与平面α的交线,分析轴线与平面的性质,可得答案.
【解答】解:本题其实就是一个平面斜截一个圆柱表面的问题,
因为三角形面积为定值,以AB为底,则底边长一定,从而可得P到直线AB的距离为定值,
分析可得,点P在以AB为轴线的圆柱面与平面α的交线上,且α与圆柱的轴线斜交,
由平面与圆柱面的截面的性质判断,可得P的轨迹为椭圆;
故选:B.
7.已知二面角α﹣AB﹣β是直二面角,P为棱AB上一点,PQ、PR分别在平面α、β内,且∠QPB=∠RPB=45°,则∠QPR为( )
A.45° B.60° C.120° D.150°
【考点】空间中直线与直线之间的位置关系;平面与平面垂直的性质.
【分析】在正方体中,又底面和侧面所成的直二面为模型,构造出满足条件的几何图形,根据正方体的几何特征,解三角形求出∠QPR可得答案.
【解答】解:以正方体的模型,构造满足条件的几何图形如下图所示
连接QR,由正方体的性质可得△PQR为等边三角形
故∠QPR=60°
故选B
8.设抛物线y2=4x的焦点为F,过点F的直线与抛物线交于A,B两点,过AB的中点M作准线的垂线与抛物线交于点P,若,则弦长|AB|等于( )
A.2 B.4 C.6 D.8
【考点】直线与圆锥曲线的关系;抛物线的简单性质.
【分析】求出抛物线焦点为F(1,0),准线为l:x=﹣1.设A(x1,y1)、B(x2,y2),直线AB的方程为y=k(x﹣1),由AB方程与抛物线方程消去y得关于x的一元二次方程,利用根与系数的关系算出:x1+x2=,x1x2=1,由此算出P的坐标为M(,),根据利用点到两点间的距离公式解出k2=2,从而算出x1+x2=4,最后根据抛物线的定义可得弦长|AB|的值.
【解答】解:∵抛物线方程为y2=4x,
∴2p=4,p=2,可得抛物线的焦点为F(1,0),准线为l:x=﹣1,
设A(x1,y1),B(x2,y2),直线AB的方程为y=k(x﹣1),
由消去y,得k2x2﹣(2k2+4)x+k2=0,
∴x1+x2=,x1x2=1,
∵过AB的中点M作准线的垂线与抛物线交于点P,
∴设P的坐标为(x0,y0),可得y0=(y1+y2),
∵y1=k(x1﹣1),y2=k(x2﹣1),
∴y1+y2=k(x1+x2)﹣2k=k•﹣2k=,
得到y0==,所以x0==,可得P(,).
∵,∴=,解之得k2=2,
因此x1+x2==4,根据抛物线的定义可得|AB|=x1+x2+p=4+2=6.
故选:C
9.在长方体ABCD﹣A1B1C1D1中,B1 C和C1D与底面A1B1C1D1所成的角分别为60°和45°,则异面直线B1C和C1D所成角的余弦值为( )
A. B. C. D.
【考点】异面直线及其所成的角.
【分析】设长方体的高为1,根据B1C和C1D与底面所成的角分别为600和450,分别求出各线段的长,将C1D平移到B1A,根据异面直线所成角的定义可知∠AB1C为异面直线B1C和DC1所成角,利用余弦定理求出此角即可.
【解答】解:设长方体的高为1,连接B1A、B1C、AC
∵B1C和C1D与底面所成的角分别为600和450,
∴∠B1CB=60°,∠C1DC=45°
∴C1D=,B1C=,BC=,CD=1则AC=
∵C1D∥B1A
∴∠AB1C为异面直线B1C和DC1所成角
由余弦定理可得cos∠AB1C=
故选A
10.已知点P是抛物线x=y2上的一个动点,则点P到点A(0,2)的距离与点P到y轴的距离之和的最小值为( )
A.2 B. C.﹣1 D. +1
【考点】抛物线的简单性质.
【分析】先求出抛物线的焦点坐标,再由抛物线的定义转化求解即可.
【解答】解:抛物线x=y2,可得:y2=4x,抛物线的焦点坐标(1,0).
依题点P到点A(0,2)的距离与点P到y轴的距离之和的最小值,就是P到(0,2)与P到该抛物线准线的距离的和减去1.
由抛物线的定义,可得则点P到点A(0,2)的距离与P到该抛物线焦点坐标的距离之和减1,
可得:﹣1=.
故选:C.
11.设P是椭圆上一点,M、N分别是两圆:(x+4)2+y2=1和(x﹣4)2+y2=1上的点,则|PM|+|PN|的最小值、最大值的分别为( )
A.9,12 B.8,11 C.8,12 D.10,12
【考点】圆与圆锥曲线的综合.
【分析】首先将P点固定于一处,设两圆心分别为C1,C2,则r1=1,r2=c且C1,C2为椭圆的焦点,PC1≤PM+MC1,PC2≤PN+NC2,PM+PN=PM+MC1+PN+NC2﹣(MC1+NC2)≥PC1+PC2﹣(MC1+NC2)=8,所以PM+PN的最小值为8.PM+PN=PM+MC1+PN+NC2﹣(MC1+NC2)≤PC1+PC2+(MC1+NC2)=12.所以PM+PN的最大值为12.
【解答】解:首先将P点固定于一处,设两圆心分别为C1,C2,
则r1=1,r2=c且C1,C2为椭圆的焦点,
PC1≤PM+MC1
PC2≤PN+NC2
PM+PN=PM+MC1+PN+NC2﹣(MC1+NC2)≥PC1+PC2﹣(MC1+NC2)
=2a﹣(r1+r2)
=10﹣2=8
所以,PM+PN的最小值为8.
PM+PN=PM+MC1+PN+NC2﹣(MC1+NC2)≤PC1+PC2+(MC1+NC2)
=2a+(r1+r2)
=10+2=12.
所以,PM+PN的最大值为12.
故选C.
12.设A1、A2为椭圆的左右顶点,若在椭圆上存在异于A1、A2的点P,使得,其中O为坐标原点,则椭圆的离心率e的取值范围是( )
A. B. C. D.
【考点】椭圆的简单性质.
【分析】由,可得 y2=ax﹣x2>0,故 0<x<a,代入=1,整理得(b2﹣a2)x2+a3x﹣a2b2=0 在(0,a )上有解,令f(x)=(b2﹣a2)x2+a3x﹣a2b2=0,结合图形,求出椭圆的离心率e的范围.
【解答】解:A1(﹣a,0),A2(a,0),设P(x,y),则=(﹣x,﹣y),=(a﹣x,﹣y),
∵,∴(a﹣x)(﹣x)+(﹣y)(﹣y)=0,y2=ax﹣x2>0,∴0<x<a.
代入=1,整理得(b2﹣a2)x2+a3x﹣a2b2=0 在(0,a )上有解,
令f(x)=(b2﹣a2)x2+a3x﹣a2b2=0,∵f(0)=﹣a2b2<0,f(a)=0,如图:
△=(a3)2﹣4×(b2﹣a2)×(﹣a2b2)=a2( a4﹣4a2b2+4b4 )=a2(a2﹣2b2)2≥0,
∴对称轴满足 0<﹣<a,即 0<<a,∴<1,
>,又 0<<1,∴<<1,故选 D.
二、填空题(本大题共4小题,共20分)
13.已知双曲线标准方程为: =1(a>0,b>0),一条渐近线方程y=3x,则双曲线的离心率是 .
【考点】双曲线的简单性质.
【分析】根据双曲线渐近线的方程进行求解即可.
【解答】解:∵线标准方程为: =1(a>0,b>0)的渐近线为为y=±x,
∴=3,
则离心率e====,
故答案为:
14.若命题“存在x∈R,ax2+4x+a≤0”为假命题,则实数a的取值范围是 (2,+∞) .
【考点】复合命题的真假.
【分析】根据所给的特称命题写出其否定命题:任意实数x,使ax2+4x+a>0,根据命题否定是假命题,得到判别式大于0,解不等式即可.
【解答】解:∵命题“存在x∈R,使ax2+4x+a≤0”的否定是
“任意实数x,使ax2+4x+a>0”
命题否定是真命题,
∴,
解得:a>2,
故答案为:(2,+∞).
15.在直角坐标系xOy中,直线l的方程为x﹣y+4=0,设点Q是曲线+y2=1上的一个动点,求它到直线l的距离的最小值为 .
【考点】椭圆的简单性质.
【分析】设Q(,sinθ),求出点Q到直线x﹣y+4=0的距离,利用三角函数性质能求出点到直线l的距离的最小值.
【解答】解:∵点Q是曲线+y2=1上的一个动点,
∴设Q(,sinθ),
点Q到直线x﹣y+4=0的距离d==,
∴当sin()=﹣1时,它到直线l的距离的最小值为.
故答案为:.
16.双曲线﹣=1(a>0,b>0)一条渐近线的倾斜角为,离心率为e,则的最小值为 2 .
【考点】双曲线的简单性质.
【分析】由双曲线渐近线的方程可知, =,离心率e==2,从而利用基本不等式即可求得的最小值.
【解答】解:∵双曲线﹣=1(a>0,b>0)的一条渐近线的倾斜角为,
∴=,
又离心率e==2,
∴==+≥2=2,
当且仅当b=3,a=,时,取得最小值2.
故答案为:2.
三、解答题(本大题共6小题,共70分)
17.已知条件p:≤﹣1,条件q:x2+x<a2﹣a,且p是q的一个必要不充分条件,求实数a的取值范围.
【考点】必要条件、充分条件与充要条件的判断.
【分析】利用不等式的解法、函数的性质分别化简命题p,q.对a分类讨论,利用简易逻辑的判定方法即可得出.
【解答】解:由解得p:﹣3≤x<1,
由x2+x<a2﹣a得(x+a)[x﹣(a﹣1)]<0,
当时,可得q:∅;
当时,可得q:(a﹣1,﹣a);
当时,可得q:(﹣a,a﹣1).
由题意得,p是q的一个必要不充分条件,
当时,满足条件;当时,(a﹣1,﹣a)⊊[﹣3,1)得,
当时,(﹣a,a﹣1)⊊[﹣3,1)得.
综上,a∈[﹣1,2].
18.已知函数
(1)若m=1,求函数f(x)的定义域.
(2)若函数f(x)的值域为R,求实数m的取值范围.
(3)若函数f(x)在区间上是增函数,求实数m的取值范围.
【考点】对数函数图象与性质的综合应用.
【分析】(1)要使函数有意义,只需真数大于零,解不等式即可得函数的定义域;
(2)若函数的值域为R,则真数应能取遍一切正数,只需y=x2﹣mx﹣m的判别式不小于零,即可解得m的范围;
(3)函数f(x)在区间上是增函数包含两层含义,y=x2﹣mx﹣m在区间上是减函数且x2﹣mx﹣m>0在区间上恒成立,分别利用二次函数的图象和性质和单调性即可解得m的范围
【解答】解:(1)若m=1,则
要使函数有意义,需x2﹣x﹣1>0,解得x∈
∴若m=1,函数f(x)的定义域为.
(2)若函数f(x)的值域为R,则x2﹣mx﹣m能取遍一切正实数,
∴△=m2+4m≥0,即m∈(﹣∞,﹣4]∪[0,+∞)
∴若函数f(x)的值域为R,实数m的取值范围为(﹣∞,﹣4]∪[0,+∞)
(3)若函数f(x)在区间上是增函数,
则y=x2﹣mx﹣m在区间上是减函数且x2﹣mx﹣m>0在区间上恒成立,
∴≥1﹣,且(1﹣)2﹣m(1﹣)﹣m≥0
即m≥2﹣2且m≤2
∴m∈
19.已知椭圆C: +=1(a>b>0)的焦距为2,长轴长为4.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)如图,过坐标原点O作两条互相垂直的射线,与椭圆C交于A,B两点.设A(x1,y1),B(x2,y2),直线AB的方程为y=﹣2x+m(m>0),试求m的值.
【考点】椭圆的简单性质.
【分析】(Ⅰ)利用椭圆C: +=1(a>b>0)的焦距为2,长轴长为4,求出椭圆的几何量,可得椭圆C的标准方程;
(Ⅱ)直线AB、联立椭圆方程,消去y,运用韦达定理,由OA⊥OB,则有x1x2+y1y2=0,化简整理即可求m的值.
【解答】解:(Ⅰ)∵椭圆C: +=1(a>b>0)的焦距为2,长轴长为4,
∴c=,a=2,
∴b=1,
∴椭圆C的标准方程为=1;
(Ⅱ)直线AB的方程为y=﹣2x+m(m>0),代入椭圆方程得
17x2﹣16mx+4m2﹣4=0,
则x1+x2=,x1x2=,①
由OA⊥OB,
知x1x2+y1y2=x1x2+(﹣2x1+m)(﹣2x2+m)
=5x1x2﹣2m(x1+x2)+m2=0,
将①代入,得5×﹣2m×+m2=0,
∵m>0,
∴m=2.
20.已知向量与.
(Ⅰ)若在方向上的投影为,求λ的值;
(Ⅱ)命题P:向量与的夹角为锐角;
命题q:,其中向量, =()(λ,α∈R).若“p或q”为真命题,“p且q”为假命题,求λ的取值范围.
【考点】向量的投影;复合命题的真假;平行向量与共线向量;数量积表示两个向量的夹角.
【分析】(Ⅰ)在方向上的投影的表达式是,由此得出关于λ的方程,解出即可.
(Ⅱ)若“p或q”为真命题,“p且q”为假命题,则pq中一真一假,分类求解,再合并即可.
【解答】解:(Ⅰ)由已知,在方向上的投影=,即=.
所以1﹣2λ=5,∴λ=﹣2.
(Ⅱ)1°,若p为真,则>0,且,即1﹣2λ>0,且λ≠﹣2.
2°若p为真,由得λ2﹣cos2α=λ+2sinα,
∴λ2﹣λ=cos2α+2sinα=1﹣sin2α+2sinα=﹣(sinα﹣1)2+2.
∵﹣1≤sinα≤1,∴﹣2≤λ2﹣λ≤2,∴﹣1≤λ≤2.
若p真q假,则∴λ<﹣1且λ≠﹣2.
若p假q真,则∴≤λ≤2
综上得λ∈(﹣∞,﹣2)∪(﹣2,﹣1)∪[,2].
21.如图,四棱锥S一ABCD中,已知AD∥BC,∠ADC=90°,∠BAD=135°,AD=DC=,SA=SC=SD=2.
(I)求证:AC⊥SD;
(Ⅱ)求二面角A﹣SB﹣C的余弦值.
【考点】二面角的平面角及求法.
【分析】(Ⅰ)取AC的中点O,连接OD,由已知得AC⊥平面SOD,由此能证明AC⊥SD.
(Ⅱ)由题意知OA=OC=OD,SA=SC=SD,从而SO⊥平面ABCD,连接BO,则∠SBO为直线SB与平面ABCD所成的角,由此能求出二面角A﹣SB﹣C的余弦值.
【解答】(Ⅰ)证明:如图,取AC的中点O,连接OD,
∵AD=DC,∴AC⊥OD,
又∵SA=SC,∴AC⊥OS,
由OD∩OS=O,得AC⊥平面SOD,
∵SD⊂平面SOD,∴AC⊥SD.
(Ⅱ)解:由题意知OA=OC=OD,
∵SA=SC=SD,
∴O是点S在平面ABCD上的射影,
故SO⊥平面ABCD,
连接BO,则∠SBO为直线SB与平面ABCD所成的角,
由题意知∠BAC=90°,∠ACB=45°,
∴△ABC为等腰直角三角形,
且AB=AC=2,∴BO=,
在Rt△SBO中,SB==2,
∴cos∠SBO==,
∴二面角A﹣SB﹣C的余弦值为.
22.已知圆C1的圆心在坐标原点O,且恰好与直线l1:x﹣2y+3=0相切,点A为圆上一动点,AM⊥x轴于点M,且动点N满足,设动点N的轨迹为曲线C.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l与椭圆C相交于不同两点A,B,且满足(O为坐标原点),求线段AB长度的取值范围.
【考点】直线与圆锥曲线的综合问题.
【分析】(Ⅰ)设出动点N(x,y),A(x0,y0),M(x0,0),由题意求圆C1的方程,结合已知,把A的坐标用N的坐标表示,代入圆的方程求得椭圆C的方程;
(Ⅱ)假设直线l的斜率存在时,设其方程为y=kx+m,联立直线方程和椭圆方程,利用,结合根浴系数的关系得到3m2=8k2+8.再利用弦长公式求得弦AB的长,利用基本不等式及函数的性质求得|AB|的范围;若直线l的斜率不存在,直接求出A,B的坐标得到|AB|的值,则线段AB长度的取值范围可求.
【解答】解:(Ⅰ)设动点N(x,y),A(x0,y0),
∵AM⊥x轴于点M,∴M(x0,0),
设圆C1 的方程为x2+y2=r2,由题意得,
∴圆C1 的方程为x2+y2=9.
由题意,,得,
∴,即,
将A()代入x2+y2=9,得动点N的轨迹方程为;
(Ⅱ)(1)假设直线l的斜率存在,设其方程为y=kx+m,
联立,可得(1+2k2)x2+4kmx+2m2﹣8=0.
∴△=64k2﹣8m2+32>0.
,(*)
∵,∴,则x1x2+(kx1+m)(kx2+m)=0,
化简可得,.
将(*)代入可得3m2=8k2+8.
又∵|AB|=.
将代入,可得=
=.
∴当且仅当,即时等号成立.
又由,∴|AB|.
∴.
(2)若直线l的斜率不存在,则OA所在直线方程为y=x,
联立,解得A(),
同理求得B(),
求得.
综上,得.