- 408.30 KB
- 2024-03-14 发布
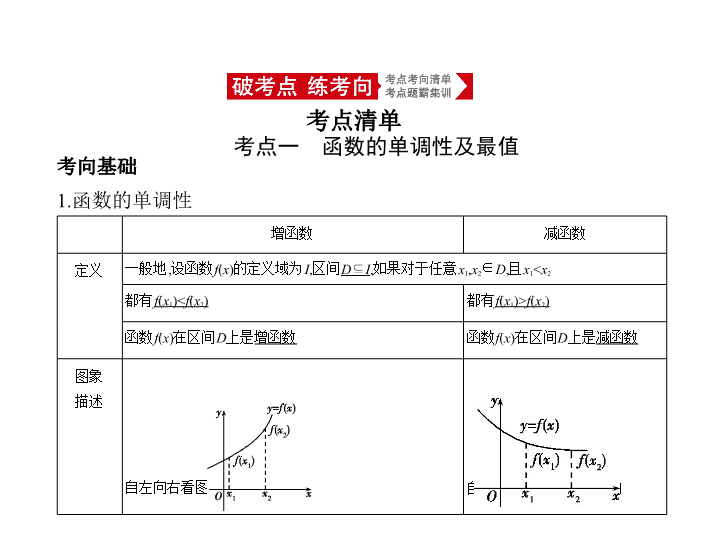
考点一 函数的单调性及最值
考点清单
考向基础
1.函数的单调性
增函数
减函数
定义
一般地,设函数
f
(
x
)的定义域为
I
,区间
D
⊆
I
,如果对于任意
x
1
,
x
2
∈
D
,且
x
1
<
x
2
都有
f
(
x
1
)<
f
(
x
2
)
都有
f
(
x
1
)>
f
(
x
2
)
函数
f
(
x
)在区间
D
上是
增函数
函数
f
(
x
)在区间
D
上是
减函数
图象
描述
自左向右看图象是
上升
的
自左向右看图象是
下降
的
注意:(1)单调函数的定义有以下两种等价形式:
∀
x
1
,
x
2
∈[
a
,
b
],且
x
1
≠
x
2
,
①
>0
⇔
f
(
x
)在[
a
,
b
]上是增函数;
<0
⇔
f
(
x
)在[
a
,
b
]上是减函数.
②(
x
1
-
x
2
)[
f
(
x
1
)-
f
(
x
2
)]>0
⇔
f
(
x
)在[
a
,
b
]上是增函数;
(
x
1
-
x
2
)[
f
(
x
1
)-
f
(
x
2
)]<0
⇔
f
(
x
)在[
a
,
b
]上是减函数.
(2)单调区间只能用区间表示,当一个函数的增区间(或减区间)有多个时,
不
能用“
∪
”连接,而应该用“和”或“,”连接
.例如:
y
=
的单调减区间为
(-
∞
,0)和(0,+
∞
),但不能写成(-
∞
,0)
∪
(0,+
∞
).
2.函数的最值
前提
一般地,设函数
y
=
f
(
x
)的定义域为
I
,如果存在实数
M
满足
条件
对于任意的
x
∈
I
,都有
f
(
x
)
≤
M
;
存在
x
0
∈
I
,使得
f
(
x
0
)=
M
对于任意的
x
∈
I
,都有
f
(
x
)
≥
M
;
存在
x
0
∈
I
,使得
f
(
x
0
)=
M
结论
M
是
f
(
x
)的
最大
值
M
是
f
(
x
)的
最小
值
考向突破
考向一 求单调区间
例1 (2017课标全国Ⅱ,8,5分)函数
f
(
x
)=ln(
x
2
-2
x
-8)的单调递增区间是
( )
A.(-
∞
,-2) B.(-
∞
,1)
C.(1,+
∞
) D.(4,+
∞
)
解析 本题主要考查复合函数的单调性.
由
x
2
-2
x
-8>0可得
x
>4或
x
<-2,
所以
x
∈(-
∞
,-2)
∪
(4,+
∞
),
令
u
=
x
2
-2
x
-8,
则其在
x
∈(-
∞
,-2)上单调递减,
在
x
∈(4,+
∞
)上单调递增.
又因为
y
=ln
u
在
u
∈(0,+
∞
)上单调递增,
所以
y
=ln(
x
2
-2
x
-8)在
x
∈(4,+
∞
)上单调递增.故选D.
答案 D
方法总结 复合函数的单调性符合同增异减的原则.
例2 (1)(2019河南郑州第一次质量预测,8)设函数
f
(
x
)=2ln(
x
+
)+3
x
3
(-2<
x
<2),则使得
f
(2
x
)+
f
(4
x
-3)>0成立的
x
的取值范围是
( )
A.(-1,1) B.
C.
D.
(2)已知
f
(
x
)是定义在(0,+
∞
)上的函数,对任意两个不相等的正数
x
1
,
x
2
,都有
>0,记
a
=
,
b
=
,
c
=
,则
( )
A.
a
<
b
<
c
B.
b
<
a
<
c
C.
c
<
a
<
b
D.
c
<
b
<
a
考向二 单调性的应用
解析 (1)由题意知
f
(
x
)的定义域关于原点对称.
f
(-
x
)=2ln(-
x
+
)-3
x
3
=-
f
(
x
),所以
f
(
x
)为奇函数,
当
x
∈(0,2)时,易知函数
f
(
x
)=2ln(
x
+
)+3
x
3
是增函数,
∴函数
f
(
x
)在(-2,2)上是增函数.
不等式
f
(2
x
)+
f
(4
x
-3)>0可转化为
f
(2
x
)>
f
(3-4
x
),由函数
f
(
x
)在(-2,2)上是增函数
得
解得
<
x
<1,故选B.
(2)∵
f
(
x
)是定义在(0,+
∞
)上的函数,对任意两个不相等的正数
x
1
,
x
2
,都有
>0,
∴
x
1
-
x
2
与
x
2
f
(
x
1
)-
x
1
f
(
x
2
)同号,
则
x
1
-
x
2
与
同号,
∴函数
y
=
是(0,+
∞
)上的增函数,
∵1<3
0.2
<2,0<0.3
2
<1,log
2
5>2,∴0.3
2
<3
0.2
0,则
f
(
x
)在R上为增函数,符合题意;
对于D,易知
f
(
x
)=ln(
-
x
)的定义域为R,
f
(-
x
)=ln(
+
x
)=-ln(
-
x
)=-
f
(
x
),则
f
(
x
)为奇函数,
设
t
=
-
x
=
,易知
t
在R上为减函数,而
y
=ln
t
为增函数,则
f
(
x
)=
ln (
-
x
) 在R上为减函数,不符合题意.故选C.
答案 C
方法2
判断函数奇偶性的方法
1.定义法
3.性质法
若
f
(
x
),
g
(
x
)在其公共定义域上具有奇偶性,则奇+奇=奇,奇
×
奇=偶,偶+偶=
偶,偶
×
偶=偶,奇
×
偶=奇.
2.图象法
例2 判断下列函数的奇偶性:
(1)
f
(
x
)=(1-
x
)
;
(2)
f
(
x
)=
(3)
f
(
x
)=
;
(4)
f
(
x
)=log
2
(
x
+
).
解析 (1)当且仅当
≥
0且1-
x
≠
0时函数有意义,
∴-1
≤
x
<1,
∴
f
(
x
)的定义域为[-1,1).
∵定义域关于原点不对称,∴函数
f
(
x
)是非奇非偶函数.
(2)易知函数
f
(
x
)的定义域为{
x
|
x
≠
0},关于原点对称,
当
x
>0时,-
x
<0,
f
(-
x
)=
x
2
-2
x
-1=-
f
(
x
);
当
x
<0时,-
x
>0,
f
(-
x
)=-
x
2
-2
x
+1=-
f
(
x
),
∴
f
(-
x
)=-
f
(
x
),∴函数
f
(
x
)是奇函数.
(3)由题意知
解得-2
≤
x
≤
2且
x
≠
0,
∴函数
f
(
x
)的定义域为[-2,0)
∪
(0,2],关于原点对称.
∴
f
(
x
)=
=
,
又
f
(-
x
)=
=-
=-
f
(
x
),
∴
f
(-
x
)=-
f
(
x
),∴函数
f
(
x
)是奇函数.
(4)解法一:易知
f
(
x
)的定义域为R.
∵
f
(-
x
)=log
2
[(-
x
)+
]=log
2
=-log
2
(
x
+
)=-
f
(
x
),∴
f
(
x
)是奇函数.
解法二:易知
f
(
x
)的定义域为R.
∵
f
(-
x
)+
f
(
x
)=log
2
[(-
x
)+
]+log
2
(
x
+
)=log
2
1=0,∴
f
(-
x
)=-
f
(
x
),
∴
f
(
x
)为奇函数.
规律总结 (1)对于解析式比较复杂的函数,有时需要将函数化简后再判
断它的奇偶性,但一定要先考虑它的定义域;
(2)对于分段函数,必须分段判断它的奇偶性,只有在每一段上都满足奇(偶)
函数的定义时,才能下相应的结论;
(3)当
f
(
x
)
≠
0时,奇偶函数定义中的判断式
f
(-
x
)=
±
f
(
x
)常被它的变式
=
±
1
所替代.
方法3
函数性质的综合应用的解题方法
求解函数性质的综合问题时,一要紧扣奇偶性、单调性、周期性的定义及
有关结论,二要充分利用各种性质之间的联系.
例3 (2019福建泉州质检,11)定义在R上的奇函数
f
(
x
)满足
f
(
x
+2)=
f
(-
x
),且当
x
∈[0,1]时,
f
(
x
)=2
x
-cos
x
,则下列结论正确的是
( )
A.
f
<
f
<
f
(2 018)
B.
f
(2 018)<
f
<
f
C.
f
(2 018)<
f
<
f
D.
f
<
f
<
f
(2 018)
解析 ∵
f
(
x
)是奇函数,∴
f
(-
x
)=-
f
(
x
),
∴
f
(
x
+2)=
f
(-
x
)=-
f
(
x
),
∴
f
(
x
+4)=-
f
(
x
+2)=
f
(
x
),
∴
f
(
x
)的周期为4,
∴
f
(2 018)=
f
(2+4
×
504)=
f
(2)=
f
(0),
f
=
f
,
f
=
f
,
∵
x
∈[0,1]时,
f
(
x
)=2
x
-cos
x
单调递增,
∴
f
(0)<
f
<
f
,
∴
f
(2 018)<
f
<
f
,故选C.
答案 C