2017-2018学年山西省朔州一中高二8月月考数学试卷 7页

朔州市一中2017-2018学年第一学期第一次阶段性考试 数学试题 一、选择题：（共60分）‎ ‎1. 下列说法中，正确的是 (　　)‎ A.棱柱的侧面可以是三角形 ‎ B.若棱柱有两个侧面是矩形，则该棱柱的其它侧面也是矩形 C.正方体的所有棱长都相等 D.棱柱的所有棱长都相等 ‎2. 已知角α的终边过点P (－4,3) ，则 的值是 ( ) ‎ A．－1 B．1 C． D． ‎ ‎3. 在等差数列中，若，是数列的前项和，则（ ）‎ ‎ A． B． C． D．‎ ‎4. 将函数的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），再将所得图像向左平移个单位，则所得函数图像对应的解析式为 （ ）.‎ A. B. C. D.‎ ‎5. 将长方体截去一个四棱锥后，得到的几何体的直观图如图所示，则该几何体的俯视图为 (　　)‎ ‎6. 函数 是 （ ）‎ A.周期为的奇函数 B.周期为的偶函数 C.周期为 的奇函数 D.周期为的偶函数 ‎7. 右图是函数在一个周期内的图象，此函数解析式为可( )‎ ‎ A． B．‎ C． ) D．‎ ‎8.已知函数在区间[2，+)上是增函数，则的取值范围是( )‎ A．（ B．（ C．（ D．（‎ ‎9. 若某几何体的三视图如图所示，则这个几何体的直观图可以是(　　)‎ ‎ ‎ ‎10. 已知水平放置的△ABC的直观图△A′B′C′(斜二测画法)是边长为a的正三角形，则原△ABC的面积为(　　)‎ A.a2 B.a2 C.a2 D.a2‎ ‎11. 设上的奇函数，且在区间（0，）上单调递增，若，三角形的内角满足，则A的取值范围是（ ）‎ ‎ A． B． C． D．‎ ‎12.已知球O，过其球面上A，B，C三点作截面，若点O到该截面的距离是球半径的一半，且AB＝BC＝2，∠B＝120°，则球O的表面积为(　　)（注:球的表面积公式S=4πr²）‎ A. B. C．4π D. 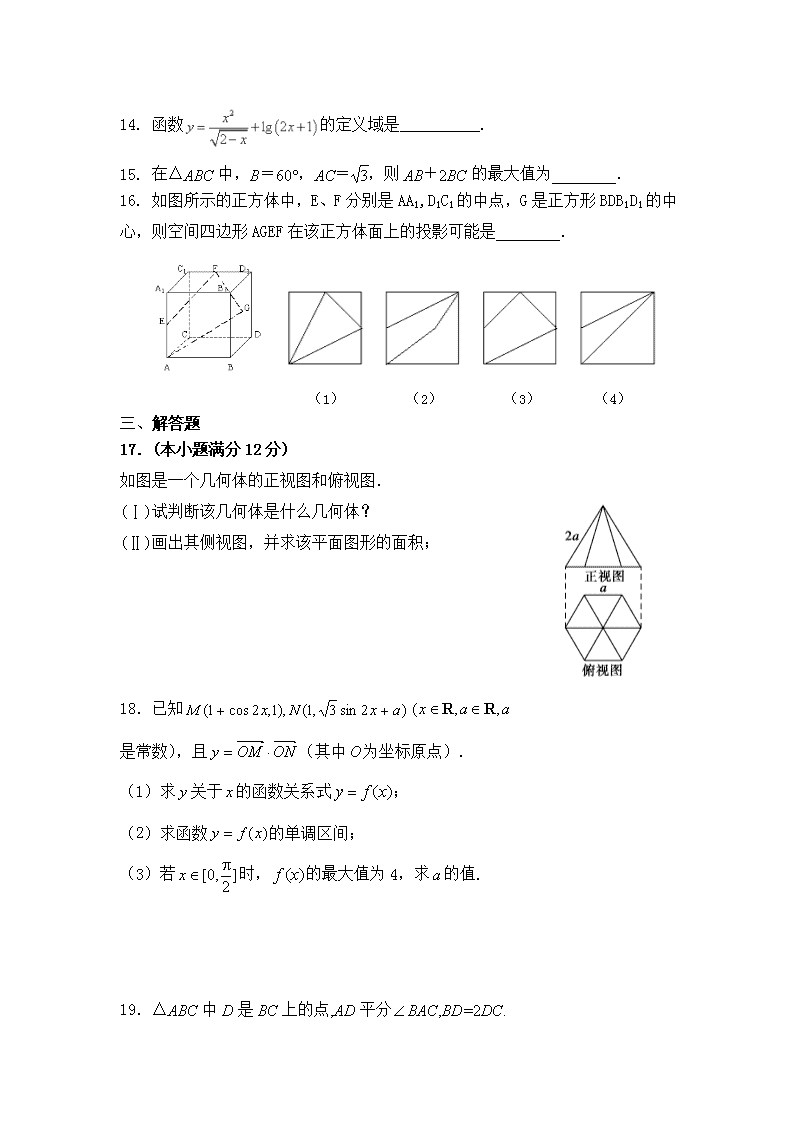二、填空题:（共20分）‎ ‎13.= __________.‎ ‎14. 函数的定义域是__________.‎ ‎15. 在△ABC中，B＝60°，AC＝，则AB＋2BC的最大值为________．‎ ‎16. 如图所示的正方体中，E、F分别是AA1,D1C1的中点，G是正方形BDB1D1的中心，则空间四边形AGEF在该正方体面上的投影可能是________．‎ ‎（1）     （2）   （3）    （4）‎ 三、解答题 ‎17．(本小题满分12分)‎ 如图是一个几何体的正视图和俯视图． ‎ ‎(Ⅰ)试判断该几何体是什么几何体？ ‎ ‎(Ⅱ)画出其侧视图，并求该平面图形的面积；‎ ‎18．已知是常数），且（其中为坐标原点）.‎ ‎（1）求关于的函数关系式；‎ ‎（2）求函数的单调区间；‎ ‎（3）若时，的最大值为4，求的值.‎ ‎19．△ABC中D是BC上的点,AD平分BAC,BD=2DC.‎ ‎（I）求 ；‎ ‎（II）若,求.‎ ‎20如图3-4-1，动物园要围成相同的长方形虎笼四间，一面可利用原有的墙，其他各面用钢筋网围成.‎ 图3-4-1‎ ‎（1）现有可围36 m长网的材料，每间虎笼的长、宽各设计为多少时，可使每间虎笼面积最大？‎ ‎（2）若使每间虎笼面积为24 m2，则每间虎笼的长、宽各设计为多少时，可使围成四间虎笼的钢筋总长度最小？‎ ‎21．设是正项数列的前项和，且 （）．‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）若，设，求数列的前项和.‎ ‎22.已知函数，，其中.‎ ‎（1）写出的单调区间（不需要证明）；‎ ‎（2）如果对任意实数，总存在实数，使得不等式成立， 求实数的取 值范围.‎ 高二数学答案 一、1.C 2.D 3.B 4.A 5.C 6. B 7. B 8.C 9.D 10.D 11.C 12.A 二、13.14.15. . 16. （1）（2）（3）‎ 三、18.解：（1），.‎ ‎（2）由（1）可得，‎ 由， 解得；‎ 由， 解得，‎ 单增区间为，单减区间为 ‎（3），因为， 所以，‎ 当，即时，取最大值，所以，即.‎ ‎19.；.‎ ‎20.解：（1）设每间虎笼长为x m，宽为y m，则由条件,知4x+6y=36，即2x+3y=18.‎ 设每间虎笼的面积为S，则S=xy.‎ 由于2x+3y≥2=2,∴2≤18,得xy≤，即S≤.‎ 当且仅当2x=3y时等号成立.‎ 由解得故每间虎笼长为4.5 m，宽为3 m时，可使面积最大.‎ ‎(2)由条件知S=xy=24.设钢筋网总长为l,则l=4x+6y.∵2x+3y≥2=2=24,‎ ‎∴l=4x+6y=2(2x+3y)≥48,当且仅当2x=3y时,等号成立.‎ 由解得故每间虎笼长6 m，宽4 m时，可使钢筋网总长最小.‎ ‎21.（Ⅰ）当时，，解得（舍去），．‎ 当时，由得，，‎ 两式作差，得，‎ 整理得，，‎ ‎，，数列为正项数列，，‎ ‎，即，数列是公差为的等差数列，‎ ‎．‎ ‎（Ⅱ），，①‎ ‎，②‎ ‎，‎ ‎22解：（1）‎ ‎①当时，的递增区间是，无减区间；‎ ‎②当时，的递增区间是,；的递减区间是；‎ ‎③当时，的递增区间是,，的递减区间是．‎ ‎（2）由题意，在上的最大值小于等于在上的最大值．‎ 当时，单调递增，∴．‎ 当时，．‎ ‎①当，即时，．由，得．∴；‎ ‎②当，即时，．‎