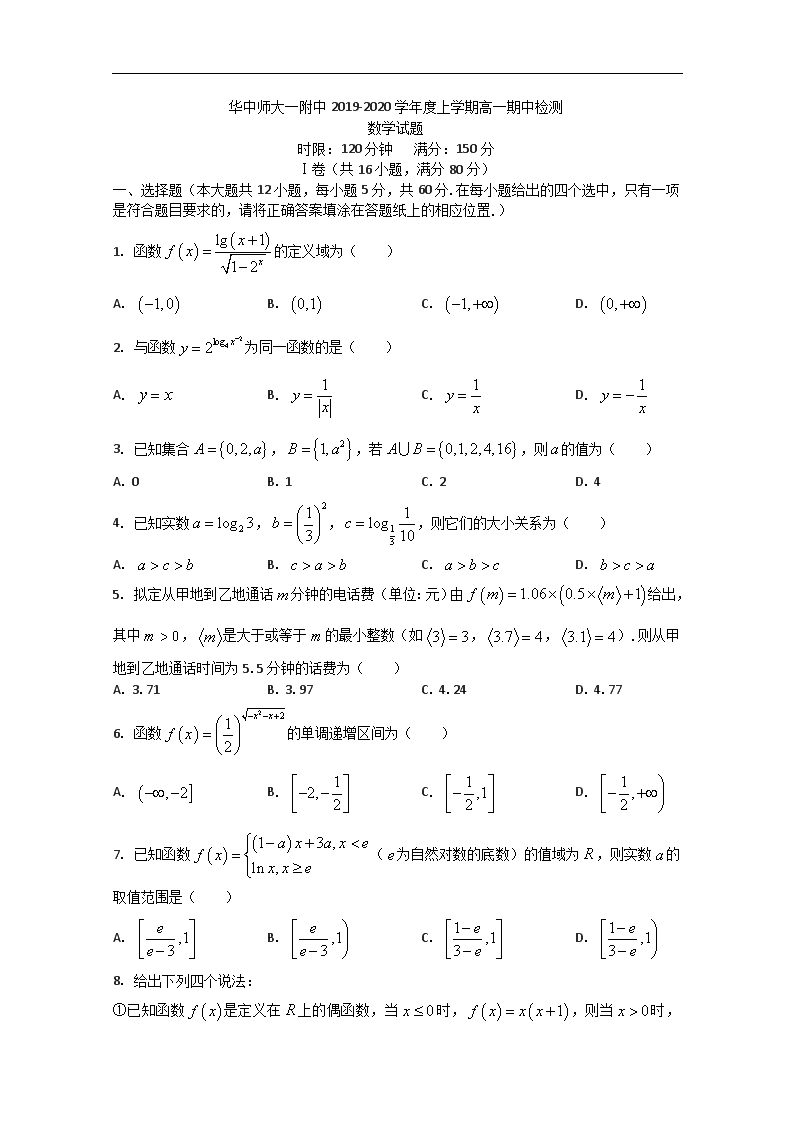- 449.50 KB
- 2024-03-12 发布
华中师大一附中2019-2020学年度上学期高一期中检测
数学试题
时限:120分钟 满分:150分
Ⅰ卷(共16小题,满分80分)
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选中,只有一项是符合题目要求的,请将正确答案填涂在答题纸上的相应位置.)
1. 函数的定义域为( )
A. B. C. D.
2. 与函数为同一函数的是( )
A. B. C. D.
3. 已知集合,,若,则的值为( )
A. 0 B. 1 C. 2 D. 4
4. 已知实数,,,则它们的大小关系为( )
A. B. C. D.
5. 拟定从甲地到乙地通话分钟的电话费(单位:元)由给出,其中,是大于或等于的最小整数(如,,).则从甲地到乙地通话时间为5.5分钟的话费为( )
A. 3.71 B. 3.97 C. 4.24 D. 4.77
6. 函数的单调递增区间为( )
A. B. C. D.
7. 已知函数(为自然对数的底数)的值域为,则实数的取值范围是( )
A. B. C. D.
8. 给出下列四个说法:
①已知函数是定义在上的偶函数,当时,,则当时,
;
②若函数的定义域为,则函数定义域为;
③若,则的取值范围为;
④函数(且)的图象必过定点.
其中正确说法的个数是( )
A. 1 B. 2 C. 3 D. 4
9. 函数的图象大致为( )
A. B. C. D.
10. 若对任意的,有,函数,则的值为( )
A. 0 B. 4 C. 6 D. 9
11. 已知定义在上的函数,,其中函数满足且在上单调递减,函数满足且在上单调递减,设函数,则对任意,均有( )
A. B.
C. D.
12. 设函数,为定义在上的奇函数,且当时,,若,则实数的取值范围是( )
A. B.
C. D.
二、填空题(本大题共4小题,每小题5分,共20分.请把结果填在答题纸上的相应位置.)
13. 化简:______.
14. 已知幂函数为偶函数,且满足,则______.
15. 已知,且,若函数有最大值,则关于的不等式的解集为______.
16. 已知且,为实数,函数,若关于的不等式恰有1个整数解,则实数的取值范围为______.
Ⅱ卷(共6小题,满分70分)
三、解答题(本大题共6小题,共70分,解答应写出文字说明过程或演算步骤,请将答案写在答题纸上的相应位置.)
17. 已知全集,集合,.
(Ⅰ)当时,求;
(Ⅱ)若,求实数的取值范围.
18. 已知.
(1)求的值;
(2)当时,求函数的最大值.
19. 某工厂生产一种仪器的元件,由于受生产能力和技术水平等因素的限制,会产生一些次品.根据经验知道,次品数(万件)与日产量(万件)之间满足函数关系:.
已知每生产1万件合格元件可盈利20万元,但每生产1万件次品将亏损10万元.(利润=盈利额-亏损额)
(1)试将该工厂每天生产这种元件所获得的利润(万元)表示为日产量(万件)的函数;
(2)当工厂将该元件的日产量(万件)定为多少时获得的日利润最大,最大日利润为多少万元?
20. 对于函数,若在定义域内存在实数满足,则称函数为“类对称函数”.
(1)判断函数是否为“类对称函数”?若是,求出所有满足条件的的值;若不是,请说明理由;
(2)若函数为定义在上的“类对称函数”,求实数的取值范围.
21. 定义在上的函数满足:①对任意恒有;②当时,,且.
(1)判断的奇偶性和单调性,并加以证明;
(2)求关于的不等式的解集.
22. 已知函数,.
(1)若存在实数,使得成立,试求的最小值;
(2)若对任意的,都有恒成立,试求的取值范围;
(3)用表示,中的最小者,设函数,讨论关于的方程的实数解的个数.