- 470.50 KB
- 2024-02-18 发布
- 1、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，可选择认领，认领后既往收益都归您。
- 2、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细先通过免费阅读内容等途径辨别内容交易风险。如存在严重挂羊头卖狗肉之情形，可联系本站下载客服投诉处理。
- 文档侵权举报QQ：3215808601
2019-2020 学年度高二第一次月考
数 学 试 卷
第 I 卷（选择题，共 60 分）
一、选择题：（本大题共 12 小题，每小题 5 分，共 60 分. 在每小题给出的四个选项中，只有
一项是符合题目要求的）
1.已知集合 A＝{x|x>1}，B＝{x|x2－2x<0}，则 A∪B 等于( )
A．{x|x>0} B．{x|x>1}
C．{x|10，b>0，且 ln(a＋b)＝0，则1
a
＋1
b
的最小值是( )
A.1
4 B．1 C．4 D．8
5.已知 m，n 表示两条不同直线，α表示平面．下列说法正确的是( )
A．若 m∥α，n∥α，则 m∥n
B．若 m⊥α，n⊂α，则 m⊥n
C．若 m⊥α，m⊥n，则 n∥α
D．若 m∥α，m⊥n，则 n⊥α
6.若点(1,1)在圆(x－a)2＋(y＋a)2＝4 的内部，则实数 a 的取值范围是( )
A．－11 或 a<－1 D．a＝±1
7.方程 x2＋y2＋ax＋2ay＋2a2＋a－1＝0 表示圆，则 a 的取值范围是( )
A．a<－2 或 a>2
3 B．－2
30}．
2．答案 B
解析 因为 sin x＝cos
5π
6 ＝－
3
2，cos x＝sin
5π
6 ＝
1
2，所以 x＝－
π
3 ＋2kπ(k∈Z)，故当 k＝1 时，
x＝
5π
3 ，即角 x 的最小正值为
5π
3 .
3．答案 C
解析 方法一 由题意可得
a1＋(a1＋6d)＝－8，
a1＋d＝2，
解得 a1＝5，d＝－3.
方法二 a1＋a7＝2a4＝－8，∴a4＝－4，
∴a4－a2＝－4－2＝2d，∴d＝－3.
4．答案 C
解析 由 a>0，b>0，ln(a＋b)＝0 得
a>0，
b>0.
故
1
a＋
1
b＝
a＋b
ab ＝
1
ab≥
a＋b
2)＝
1
2)＝4.
当且仅当 a＝b＝
1
2时上式取“＝”．
5．答案 B
解析 若 m∥α，n∥α，则 m，n 可能平行、相交或异面，A 错；
若 m⊥α，n⊂α，则 m⊥n，因为直线与平面垂直时，它垂直于平面内任一直线，B 正确；
若 m⊥α，m⊥n，则 n∥α或 n⊂α，C 错；
若 m∥α，m⊥n，则 n 与α可能相交，可能平行，也可能 n⊂α，D 错．
6．答案 A
解析 ∵点(1,1)在圆的内部，
∴(1－a)2＋(1＋a)2<4，∴－10，
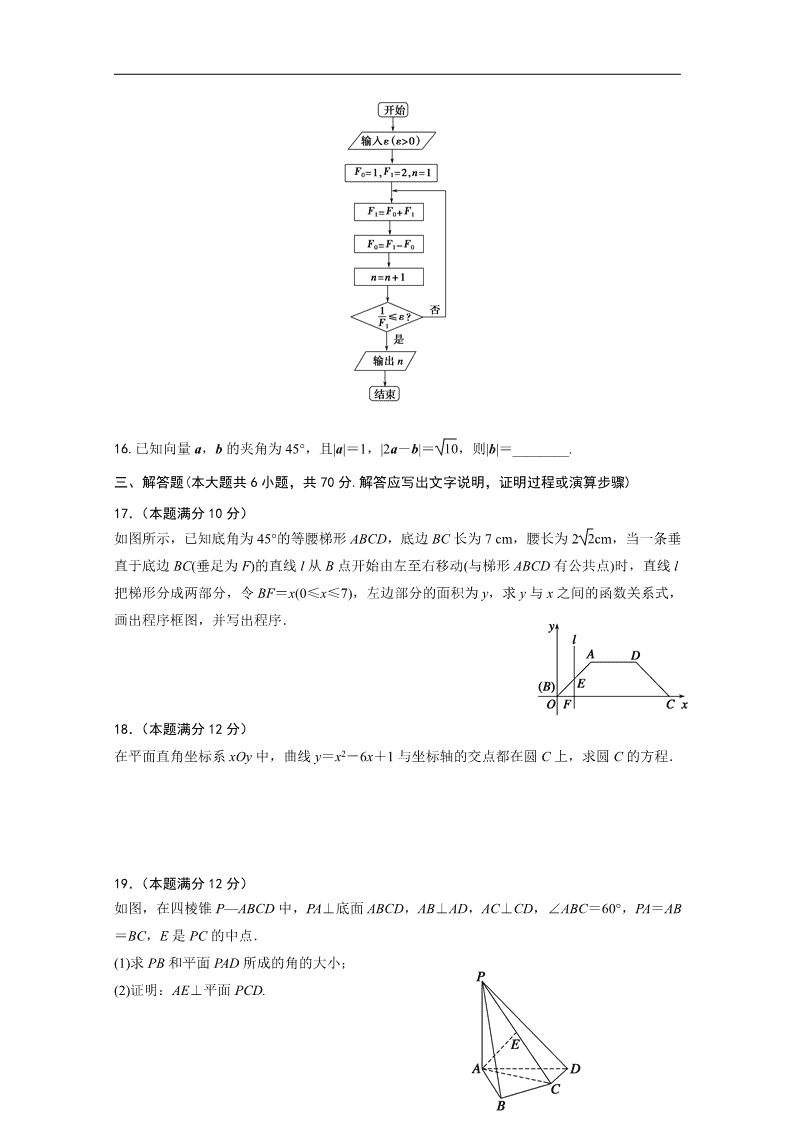
解得－20，
－x2－3x＋4>0，得－1＝0 AND x<＝2 THEN
y＝0.5 *x^2
ELSE
IF x<＝5 THEN
y＝2*x-2
ELSE
y =-0.5*(x-7) ^2+10
END IF
END IF
PRINT y
END
18．解 (代数法)曲线 y＝x2－6x＋1 与 y 轴的交点为(0,1)，与 x 轴的交点为(3＋2，0)，(3－2，
0)，设圆的方程是 x2＋y2＋Dx＋Ey＋F＝0 (D2＋E2－4F>0)，
则有＋F＝0，,)＋F＝0，)解得
E＝－2，
F＝1，
故圆的方程是 x2＋y2－6x－2y＋1＝0.
(几何法)曲线 y＝x2－6x＋1 与 y 轴的交点为(0,1)，与 x 轴的交点为(3＋2，0)，(3－2，0)．
故可设 C 的圆心为(3，t)，则有 32＋(t－1)2＝(2)2＋t2，
解得 t＝1.则圆 C 的半径为＝3，
所以圆 C 的方程为(x－3)2＋(y－1)2＝9.
19．(1)解 在四棱锥 P—ABCD 中，
因为 PA⊥底面 ABCD，AB⊂平面 ABCD，
故 PA⊥AB.又 AB⊥AD，PA∩AD＝A，
从而 AB⊥平面 PAD，
故 PB 在平面 PAD 内的射影为 PA，
从而∠APB 为 PB 和平面 PAD 所成的角．
在 Rt△PAB 中，AB＝PA，故∠APB＝45°.
所以 PB 和平面 PAD 所成的角的大小为 45°.
(2)证明 在四棱锥 P—ABCD 中，
因为 PA⊥底面 ABCD，CD⊂平面 ABCD，
故 CD⊥PA.由条件 CD⊥AC，PA∩AC＝A，
∴CD⊥平面 PAC.
又 AE⊂平面 PAC，∴AE⊥CD.
由 PA＝AB＝BC，∠ABC＝60°，可得 AC＝PA.
∵E 是 PC 的中点，∴AE⊥PC.
又 PC∩CD＝C，综上得 AE⊥平面 PCD.
20．解 (1)由 f(x＋2)＝－f(x)得，
f(x＋4)＝f[(x＋2)＋2]＝－f(x＋2)＝f(x)，
所以 f(x)是以 4 为周期的周期函数，
∴f(π)＝f(－1×4＋π)＝f(π－4)＝－f(4－π)
＝－(4－π)＝π－4.
(2)由 f(x)是奇函数与 f(x＋2)＝－f(x)，
得：f[(x－1)＋2]＝－f(x－1)＝f[－(x－1)]，
即 f(1＋x)＝f(1－x)．
故知函数 y＝f(x)的图象关于直线 x＝1 对称．
又当 0≤x≤1 时，f(x)＝x，且 f(x)的图象关于原点成中心对称，则 f(x)的图象如图所示．
当－4≤x≤4 时，f(x)的图象与 x 轴围成的图形面积为 S，
则 S＝4S△OAB＝4×
1
×2×1＝4.
21．解 (1)由已知，有 f(x)＝cos x·(
1
2sin x＋
3
2cos x)－cos2x＋
3
4
＝
1
2sin x·cos x－
3
2cos2x＋
3
4
＝
1
4sin 2x－
3
4(1＋cos 2x)＋
3
4
＝
1
4sin 2x－
3
4cos 2x
＝
1
2sin(2x－
π
3 )．
所以 f(x)的最小正周期 T＝
2π
2 ＝π.
(2)因为 f(x)在区间[－
π
4 ，－
π
12]上是减函数，在区间[－
π
12，
π
4 ]上是增函数，
f(－
π
4 )＝－
1
4，f(－
π
12)＝－
1
2，f(
π
4 )＝
1
4，
所以，函数 f(x)在闭区间[－
π
4 ，
π
4 ]上的最大值为
1
4，最小值为－
1
2.
22．
(1)证明 由 a1＝1 及 Sn＋1＝4an＋2，
有 a1＋a2＝S2＝4a1＋2.
∴a2＝5，∴b1＝a2－2a1＝3.
又
Sn＋1＝4an＋2， ①
Sn＝4an－1＋2， ②
①－②，得 an＋1＝4an－4an－1，
∴an＋1－2an＝2(an－2an－1)．
∵bn＝an＋1－2an，∴bn＝2bn－1，
故{bn}是首项 b1＝3，公比为 2 的等比数列．
(2)解 由(1)知 bn＝an＋1－2an＝3·2n－1，
∴
an＋1
2n＋1－
an
2n＝
3
4，
故{
an
2n}是首项为
1
2，公差为
3
4的等差数列．
∴
an
2n＝
1
2＋(n－1)·
3
4＝
3n－1
4 ，
得 an＝(3n－1)·2n－2.
您可能关注的文档
- 安徽省潜山第二中学2019-2020学年高二上学期第一次月考数学试题 含答案
- 2020年电工技师工作总结范文
- 专题12 正确使用词语（包括熟语）-2017年高考语文二轮核心考点总动员
- 英语卷·2018届广东省深圳市普通高中学校高考高三12月月考（07）（2017-12）Word版
- 人教版化学选修六《2_1物质的分离和提纯（第1课时）》课件
- 2017-2018学年福建省莆田市第二十四中学高二下学期第一次月考英语试题 Word版
- 静安区高考化学一模精装带答案
- 安全生产月工作计划报告_安全工作计划_
- 专题15+机械振动和机械波（测）-2019年高考物理二轮复习讲练测
- 河南省开封高中2012届高三上学期试题（物理）
