- 170.50 KB
- 2024-02-14 发布
鲁教版数学九年级上册期末测试题
(时间:90分钟 分值:120分)
一、选择题(每题4分,共40分)
1.下面四个关系式中,y是x的反比例函数的是( )
A.y= B.yx=﹣ C.y=5x+6 D.=
2. y=(m2﹣m)是反比例函数,则( )
A.m≠0 B.m≠0且m≠1 C.m=2 D.m=1或2
3.已知反比例函数y=﹣,下列结论不正确的是( )
A.图象必经过点(﹣1,2) B.y随x的增大而增大
C.图象在第二、四象限内 D.若x>1,则0>y>﹣2
4.如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数y=(x>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C、D.QD交PA于点E,随着m的增大,四边形ACQE的面积( )
A. 减小 B.增大 C.先减小后增大 D.先增大后减小
5.在△ABC中,∠C=90°,下列各式不成立的是( )
A.a=b∙cosA B.a=c∙cosB C.c= D.a=b∙tanA
6.如图,为了测量河岸A,B两点的距离,在与AB垂直的方向上取点C,测得AC=a,∠ABC=α,那么AB等于( )
A.a•sinα B.a•cosα C.a•tanα D.
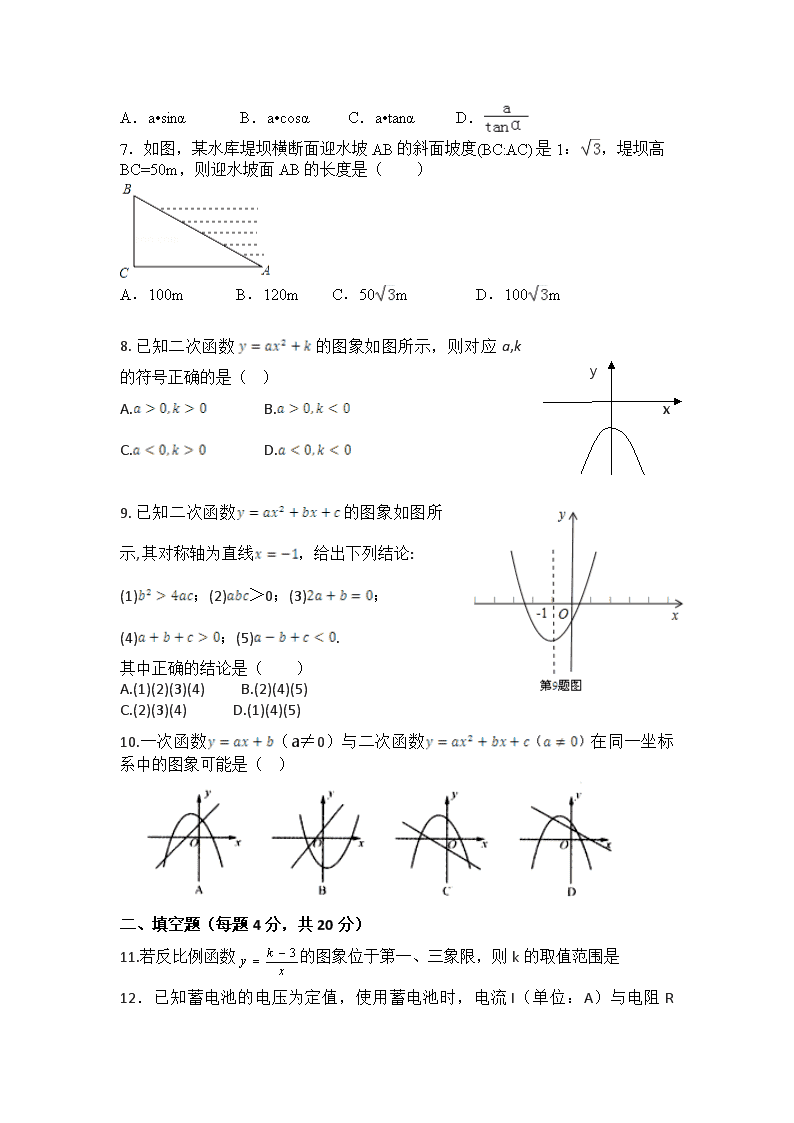
7.如图,某水库堤坝横断面迎水坡AB的斜面坡度(BC:AC)是1:,堤坝高BC=50m,则迎水坡面AB的长度是( )
A.100m B.120m C.50m D.100m
x
y
8. 已知二次函数的图象如图所示,则对应a,k的符号正确的是( )
A. B.
C.
D.
9. 已知二次函数的图象如图所示,其对称轴为直线,给出下列结论:
(1);(2)>0;(3);
(4);(5).
其中正确的结论是( )
A.(1)(2)(3)(4) B.(2)(4)(5)
C.(2)(3)(4) D.(1)(4)(5)
10.一次函数(a≠0)与二次函数在同一坐标系中的图象可能是( )
二、填空题(每题4分,共20分)
11.若反比例函数的图象位于第一、三象限,则k的取值范围是
12
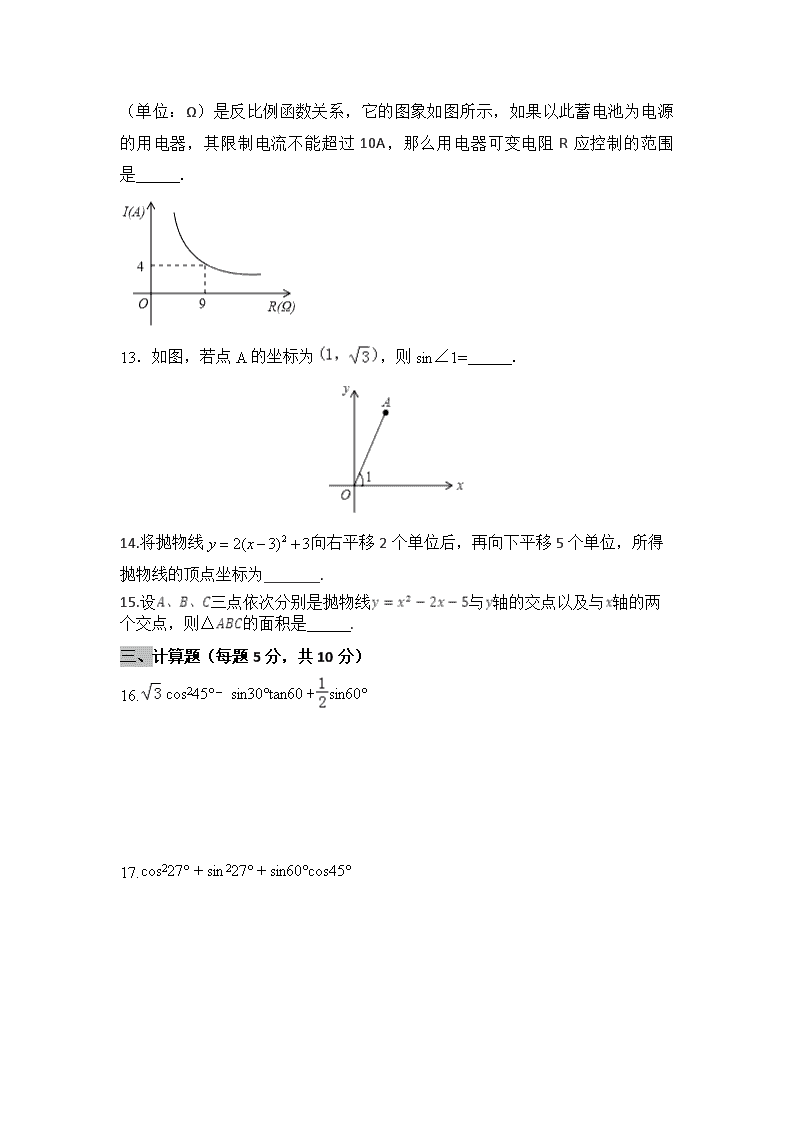
.已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示,如果以此蓄电池为电源的用电器,其限制电流不能超过10A,那么用电器可变电阻R应控制的范围是 .
13.如图,若点A的坐标为,则sin∠1= .
14.将抛物线向右平移2个单位后,再向下平移5个单位,所得抛物线的顶点坐标为_______.
15.设三点依次分别是抛物线与轴的交点以及与轴的两个交点,则△的面积是 .
三、计算题(每题5分,共10分)
16. cos245°﹣sin30°tan60+sin60°
17. cos227° + sin227° + sin60°cos45°
四、解答题
16. (7分)画出的图象,并写出函数的增减性.
17. (9分)已知反比例函数(k为常数,k≠1).
(1)其图象与正比例函数的图象的一个交点为点P,若点P的纵坐标是2,求k的值;
(2)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(3)若其图象的一支位于第二象限,在这一支上任取两点A(x1,y1)、B(x2,y2),当y1>y2时,试比较x1与x2的大小.
20.(9分)据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.
21.(8分)已知函数的图象经过点(3,2).
(1)求这个函数的关系式;
(2)画出它的图象,并指出图象的顶点坐标;
(3)当时,求使得的的取值范围.
22.(7分)商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当的降价措施,经调查发现,每件商品每降价1元,商场平均每天可多售出2件,据此规律,请回答:
(1)设每件商品降价x元,此商品可多售出 件,此商品每件盈利 元此商品每天可销售 件.
(2)每件商品降价多少元时,商场日盈利可达到2100元?
23.(10分)如图,反比例函数y=的图象与一次函数y=ax﹢b的图象交于C(4,﹣3),E(﹣3,4)两点.且一次函数图象交y轴于点A.
(1)求反比例函数与一次函数的解析式;
(2)求△COE的面积;
(3)点M在x轴上移动,是否存在点M使△OCM为等腰三角形?若存在,请你直接写出M点的坐标;若不存在,请说明理由.
参考答案
一. DCBBA DADDC
二. 11.k>3
12. R≥3.6Ω
13.
14. (5,-2)
15. 5√6
三. 16.
17.1+
四.
18.图像略 增减性:当x>0时,y随x的增大而增大
当x<0时,y随x的增大而增大
19.
(1)k=5
(2)k>1
(3)x1>x2
20.
(1)20m
(2) 未超速
21.
(1) y=x2-2x-1
(2) 顶点坐标为(1,-2)
(3) x≥3
22.
(1)2x 50-x 30+2x
(2)15或20元
23.
(1) y= y=-x+1
(2) 3.5
(3) (5,0)、(-5,0)、(8,0)、(,0)