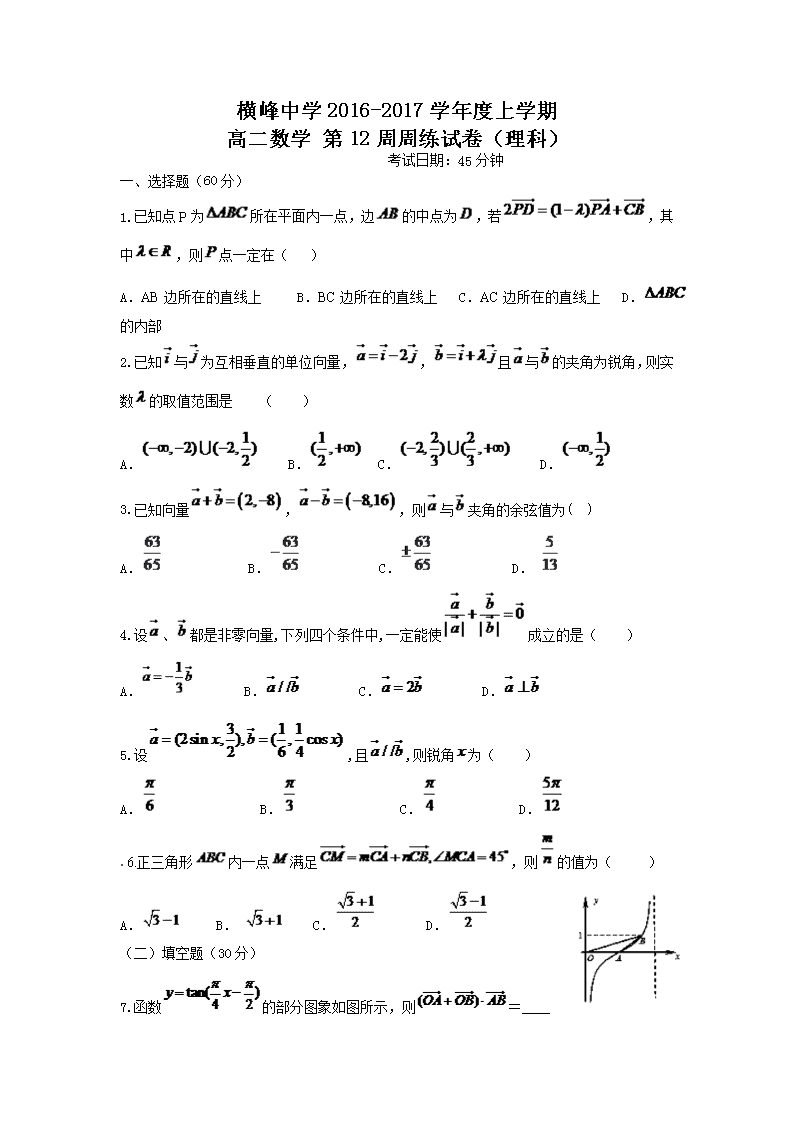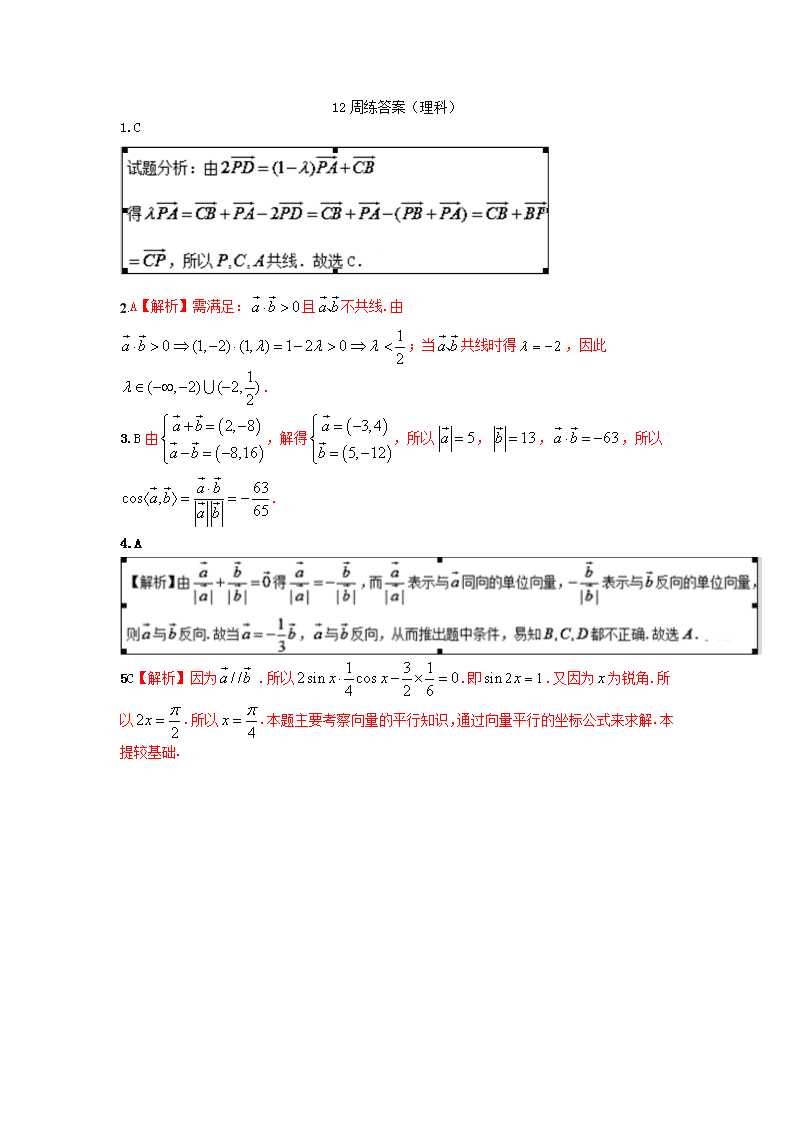- 1.12 MB
- 2024-02-04 发布
横峰中学2016-2017学年度上学期
高二数学 第12周周练试卷(理科)
考试日期:45分钟
一、选择题(60分)
1.已知点P为所在平面内一点,边的中点为,若,其中,则点一定在( )
A.AB边所在的直线上 B.BC边所在的直线上 C.AC边所在的直线上 D.的内部
2.已知与为互相垂直的单位向量,,且与的夹角为锐角,则实数的取值范围是 ( )
A. B. C. D.
3.已知向量,,则与夹角的余弦值为( )
A. B. C. D.
4.设、都是非零向量,下列四个条件中,一定能使成立的是( )
A. B. C. D.
5.设,且,则锐角为( )
A. B. C. D.
.6.正三角形内一点满足,则的值为( )
A. B. C. D.
(二)填空题(30分)
7.函数的部分图象如图所示,则=____
8.若O为△ABC所在平面内任一点,且满足,则△ABC的形状为___
9.在平面直角坐标系中,是坐标原点,两定点满足,则点集所表示的区域的面积是___________
【来源:全,品…中&高*考+网】10在△ABC中,内角A,B,C所对的边分别为a,b,c,且a+b+c=8.
(1)若a=2,b=,求cos C的值;
(2)若sin A+sin B=2sin C,且△ABC的面积S=sin C,求a和b的值.
11.设平面向量,.若存在实数和角,
使向量,,且.
(I)求函数的关系式; (II)令,求函数的极值.
12周练答案(理科)
1.C
2.A【解析】需满足:且不共线.由;当共线时得,因此.
3.B由,解得,所以,,,所以.
4.A
5C【解析】因为 .所以.即.又因为为锐角.所以.所以.本题主要考察向量的平行知识,通过向量平行的坐标公式来求解.本提较基础.
6D
7.【答案】B
8..C【解析】因为,
即,
所以是等腰三角形,选C.
9..
10.
11. 解:(I)由,,得
=,即,得
.
(II)由,得
求导得,令,得,
当,,为增函数;当时,,为减函数;
当时,,为增函数.
所以当,即时,有极大值;当,即时,有极小
值.