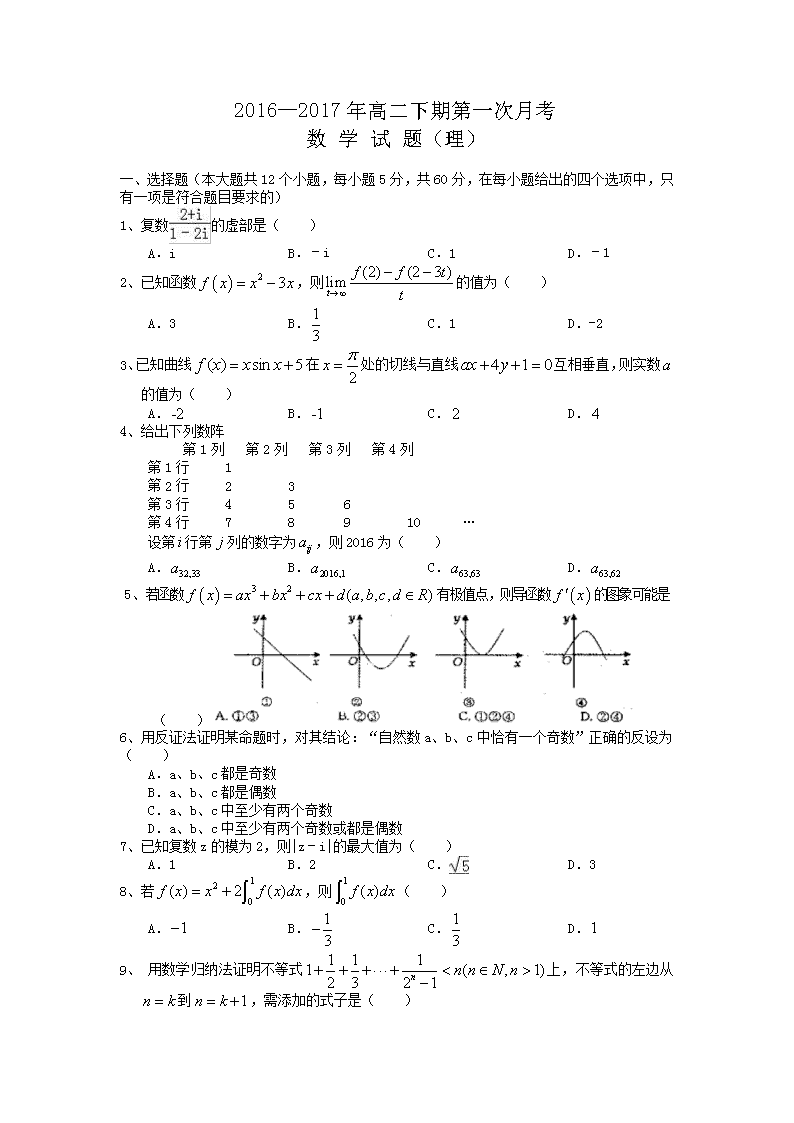- 878.00 KB
- 2024-01-29 发布
www.ks5u.com
2016—2017年高二下期第一次月考
数 学 试 题(理)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1、复数的虚部是( )
A.i B.﹣i C.1 D.﹣1
2、已知函数,则的值为( )
A.3 B. C.1 D.-2
3、已知曲线在处的切线与直线互相垂直,则实数的值为( )
A. B. C. D.
4、给出下列数阵
第1列 第2列 第3列 第4列
第1行 1
第2行 2 3
第3行 4 5 6
第4行 7 8 9 10 …
设第行第列的数字为,则2016为( )
A. B. C. D.
5、若函数有极值点,则导函数的图象可能是( )
6、用反证法证明某命题时,对其结论:“自然数a、b、c中恰有一个奇数”正确的反设为( )
A.a、b、c都是奇数
B.a、b、c都是偶数
C.a、b、c中至少有两个奇数
D.a、b、c中至少有两个奇数或都是偶数
7、已知复数z的模为2,则|z﹣i|的最大值为( )
A.1 B.2 C. D.3
8、若,则( )
A. B. C. D.
9、 用数学归纳法证明不等式上,不等式的左边从到,需添加的式子是( )
A. B.
C. D.
10.已知是定义在R上的函数,其导函数满足,则( )
A.
B.
C.
D.
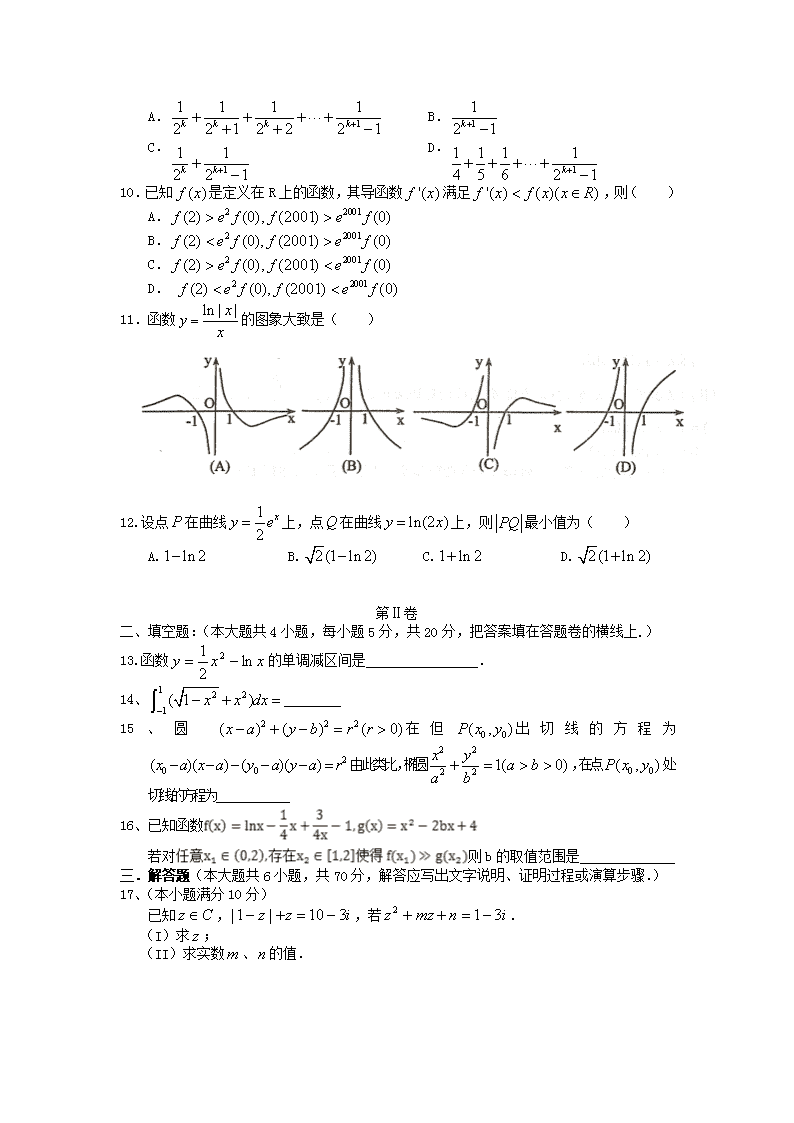
11.函数的图象大致是( )
12.设点在曲线上,点在曲线上,则最小值为( )
A. B. C. D.
第Ⅱ卷
二、填空题:(本大题共4小题,每小题5分,共20分,把答案填在答题卷的横线上.)
13.函数的单调减区间是 .
14、
15、圆 在但出切线的方程为 由此类比,椭圆,在点处切线的方程为
16、已知函数
若对则b的取值范围是
三.解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤.)
17、(本小题满分10分)
已知,,若.
(I)求;
(II)求实数、的值.
18、已知a,b是正实数,证明:。
19、(本小题满分12分)
已知函数在与时都取得极值.
(1)求、的值及函数的单调区间;
(2)若对,不等式恒成立,求的取值范围.
20、已知曲线f(x)=ax 2+2在x=1处的切线与2x﹣y+1=0平行.
(1)求f(x)的解析式;
(2)求由曲线y=f(x)与y=3x,x=0,x=2所围成的平面图形的面积.
21、(本小题满分12分)
是否存在常数,使等式对于一切都成立?若不存在,说明理由;若存在,请证明之?
22、已知函数.
(1)求函数的极值;
(2)若,试讨论关于的方程的解的个数,并说明理由.
高二理科数学第一次月考参考答案
一、 选择题:
1-5CADCC; 6-10.DDBAD 11.C 12.B
二、 填空题:
13,(0,1);14、 ;15、=1; 16、
三、解答题:
17.(1);……………………………………………5分
(2)……………………………………………………10分
18.证明:要证: 可证:
即证:
即证:
可证: 只须证:
而 故只须证
上式显然成立 以上各步均可逆,故
19.解:(1),
,
又因为 在与时都取得极值,
所以与是方程的两根,
由韦达定理,得
. ……………………………………………4分
所以,
由,得 ;
由,得,
所以的单调增区间为,减区间为.……6分
(2)当变化时,的变化如下表
1
+
0
—
0
+
单调递增
极大值
单调递减
极小值
单调递增
所以,当时, 有极大值 ,
且 , ,
所以当,最大值为,
所以,即. …………………………………… 12分
20.解:(1)y'=2ax,于是切线的斜率k=y'|x=1=2a,∵切线与直线2x﹣y+1=0平行
∴2a=2∴a=1
故f (x )的解析式f (x )=x 2+2.
(2)联立,解得x1=1,x2=2
∴S=∫01(x2+2﹣3x)dx+∫12(3x﹣x2﹣2)dx=+=1
所围成的平面图形的面积1.
21、解:若存在常数使等式成立,则将代入上式,有
得,即有对于一切成立………4分
证明如下:
(1)当时,左边=,右边=,所以等式成立…………6分(2)假设时等式成立,
当
=
==
==
也就是说,当时,等式成立,
综上所述,可知等式对任何都成立。 …………12分
22、解:
(2)令,,问
题等价于求函数的零点个数.