- 255.50 KB
- 2024-01-22 发布
周周练(24.1)
(时间:45分钟 满分:100分)
一、选择题(每小题4分,共40分)
1.下列说法正确的是(B)
A.平分弦的直径垂直于弦
B.半圆(或直径)所对的圆周角是直角
C.相等的圆心角所对的弧相等
D.相等的弦所对的圆心角相等
2.如图,在⊙O中,=,∠ADC=20°,则∠AOB的度数是(A)
A.40° B.30° C.20° D.15°
3.如图,在⊙O中,弦的条数是(C)
A.2 B.3
C.4 D.以上均不正确
4.如图,AB是⊙
6
O的直径,点C、D在⊙O上,且点C、D在AB的异侧,连接AD、OD、OC.若∠AOC=70°,且AD∥OC,则∠AOD的度数为(D)
A.70° B.60° C.50° D.40°
5.如图,在Rt△ABC中,∠ACB=90°,∠A=56°.以BC为直径的⊙O交AB于点D.E是⊙O上一点,且=,连接OE.过点E作EF⊥OE,交AC的延长线于点F,则∠F的度数为(C)
A.92° B.108° C.112° D.124°
6.在⊙O中,∠AOB=84°,则弦AB所对的圆周角的度数为(D)
A.42° B.138°
C.69° D.42°或138°
7.数学课上,老师让测量三角形纸板中∠ACB的度数,小周把三角形纸板按如图所示的方式放置在一个破损的量角器上,使点C落在半圆上,点A,B处的读数分别为65°,20°,则∠ACB的度数为(C)
A.45° B.32.5°
C.22.5° D.20°
8.如图,在⊙O中,=,直径CD⊥AB于点N,P是上一点,则∠BPD的度数是(A)
A.30° B.45°
C.60° D.15°
9.如图,点A,B,C是⊙O上的三点,且四边形ABCO是平行四边形,OF⊥AB交⊙O于点F,则∠BAF等于(B)
6
A.12.5° B.15°
C.20° D.22.5°
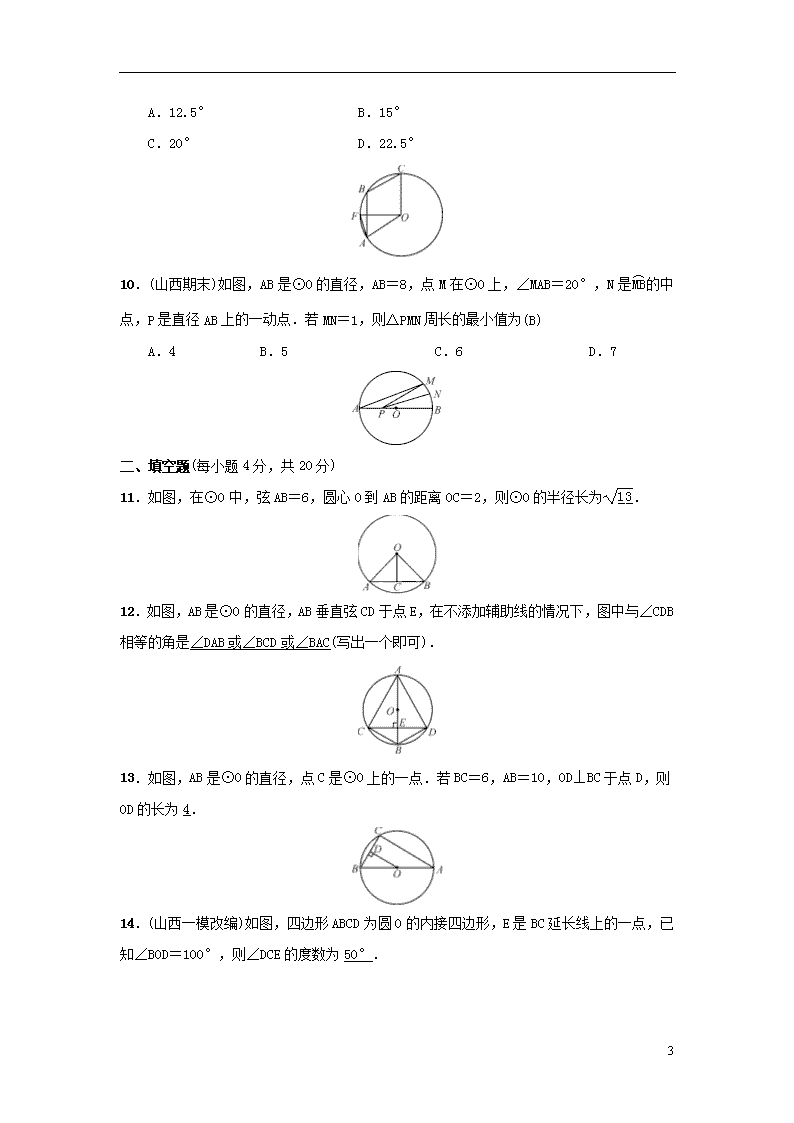
10.(山西期末)如图,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是的中点,P是直径AB上的一动点.若MN=1,则△PMN周长的最小值为(B)
A.4 B.5 C.6 D.7
二、填空题(每小题4分,共20分)
11.如图,在⊙O中,弦AB=6,圆心O到AB的距离OC=2,则⊙O的半径长为.
12.如图,AB是⊙O的直径,AB垂直弦CD于点E,在不添加辅助线的情况下,图中与∠CDB相等的角是∠DAB或∠BCD或∠BAC(写出一个即可).
13.如图,AB是⊙O的直径,点C是⊙O上的一点.若BC=6,AB=10,OD⊥BC于点D,则OD的长为4.
14.(山西一模改编)如图,四边形ABCD为圆O的内接四边形,E是BC延长线上的一点,已知∠BOD=100°,则∠DCE的度数为50°.
6
15.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16厘米,则球的半径为10厘米.
三、解答题(共40分)
16.(8分)如图,AB是⊙O的直径,点C,D是⊙O上的两点,且AC=CD.求证:OC∥BD.
证明:∵AC=CD,
∴=.
∴∠ABC=∠DBC.
∵OC=OB,
∴∠OCB=∠OBC.
∴∠OCB=∠DBC.
∴OC∥BD.
17.(10分)如图,将一个两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D,E,量出半径OC=5 cm,弦DE=8 cm,求直尺的宽.
解:过点O作OM⊥DE于点M,连接OD.
6
∴DM=DE.
∵DE=8 cm,∴DM=4 cm.
在Rt△ODM中,∵OD=OC=5 cm,
∴OM===3(cm).
∴直尺的宽度为3 cm.
18.(10分)如图,圆内接四边形ABDC中,AB是⊙O的直径,BE=CE.
(1)请写出四个不同类型的正确结论;
(2)若BE=4,AC=6,求DE的长.
解:(1)不同类型的正确结论为:BE=BC,=,∠BED=90°,BD=CD,OD⊥BC,△BOD是等腰三角形,△BDE≌△CDE,OB2=OE2+BE2等等.
(2)∵AB是⊙O的直径,∴OA=OB.
∵BE=CE,∴OD⊥BC,OE为△ABC的中位线.
∴OE=AC=×6=3.
在Rt△OBE中,由勾股定理,得OB===5.
∵OD=OB=5.
∴DE=OD-OE=5-3=2.
19.(12分)如图所示,正方形ABCD内接于⊙O,在劣弧上取一点E,连接DE,BE,过点D作DF∥BE交⊙O于点F,连接BF,AF,且AF与DE相交于点G,求证:
(1)四边形EBFD是矩形;
(2)DG=BE.
6
证明:(1)∵正方形ABCD内接于⊙O,
∴∠BED=∠BAD=90°,∠BFD=∠BCD=90°.
∵DF∥BE,∴∠EDF+∠BED=180°.∴∠EDF=90°.
∴四边形EBFD是矩形.
(2)连接AC.
∵四边形ABCD是正方形,∴∠ACD=45°.
∴∠AFD=∠ACD=45°.
又∵∠GDF=90°,∴∠DGF=∠DFG=45°.
∴DG=DF.
又∵在矩形EBFD中,BE=DF,
∴DG=BE.
6