- 409.00 KB
- 2024-01-17 发布
2017-2018学年重庆市巫溪中学高二上学期第一次月考
数 学 试 题 (理科)
一、选择题(本大题共12小题,每小题5分,共60分)
1.若α∥β,a⊂α,b⊂β,则a与b的位置关系是( )
A.平行或异面 B.相交 C.异面 D.平行
2.l1,l2,l3是空间三条不同的直线,则下列命题正确的是( )
A.l1⊥l2,l2⊥l3⇒l1∥l3 B.l1⊥l2,l2∥l3⇒l1⊥l3
C.l1∥l2∥l3⇒l1,l2,l3共面 D.l1,l2,l3共点⇒l1,l2,l3共面
3.一个球的内接正方体的表面积为54,则球的表面积为( )
A.9π B.18π C.27π D.54π
4.(原创)一个几何体的三视图是通过怎样的投影而得到的( )
A.中心投影 B.平行投影 C.中心和平行投影 D.以上都不对
5.将边长为a的正方形ABCD沿对角线AC折起,使得BD=a,则三棱锥DABC的体积为( )
(A)a3 (B) a3 +1 (C)2a3 (D)3a
6.在四面体ABCD中,棱AB,AC,AD两两互相垂直,则顶点A在底面BCD上的投影H为△BCD的( )
A.垂心 B.重心 C.外心 D.内心
7.若空间中四点A、B、C、D不共面,且这四点到平面的距离都相等,则满足此条件的不同平面有( )个
A. 4 B.5 C.6 D.7
8.某几何体的三视图如下图所示,则该几何体的表面积为( )
A.54 B.60 C.66 D.72
9.如图, 已知三棱柱的侧棱与底面边长都相等,在底面上的射影为的中点,则异面直线与所成的角的余弦值为( )
A. B. C. D.
10.如图,在正方体中,点为线段的中点,设点在线段上,直线与平面所成的角为,则的取值范围是 ( )
A. B. C. D.
11. (原创)把四个半径都是1的小球中的三个小球放在桌面上,使它们两两相切,然后在它们上面放上第四个小球,使它与前三个都相切,则第四个小球的最高点与桌面的距离是( )
A. B. C. D.
12(原创)已知四面体中,,则该四面体的体积为( )
A.20 B.40 C. 60 D.
二、填空题(本大题共4小题,每小题5分,共20分)
13.(原创)已知正三角形ABC的边长为,在斜二则画法下其所对应的三角形A′B′C′ 的面积是_______
14.三棱锥中,分别为的中点,记三棱锥的体积为,的体积为,则
15.已知三棱锥中,、、两两互相垂直,且PA=3,PB=4, PC =5,则三棱锥的外接球的表面积为
16. 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为__________
三、解答题(本大题共6小题,共70分)
17.(本小题满分10分)如图所示,空间四边形ABCD,E、F分别是AB、AD的中点,G、H分别是BC、CD上的点,且CG=BC,CH=DC.求证:
(1) E、F、G、H四点共面;
(2)三直线FH、EG、AC共点.
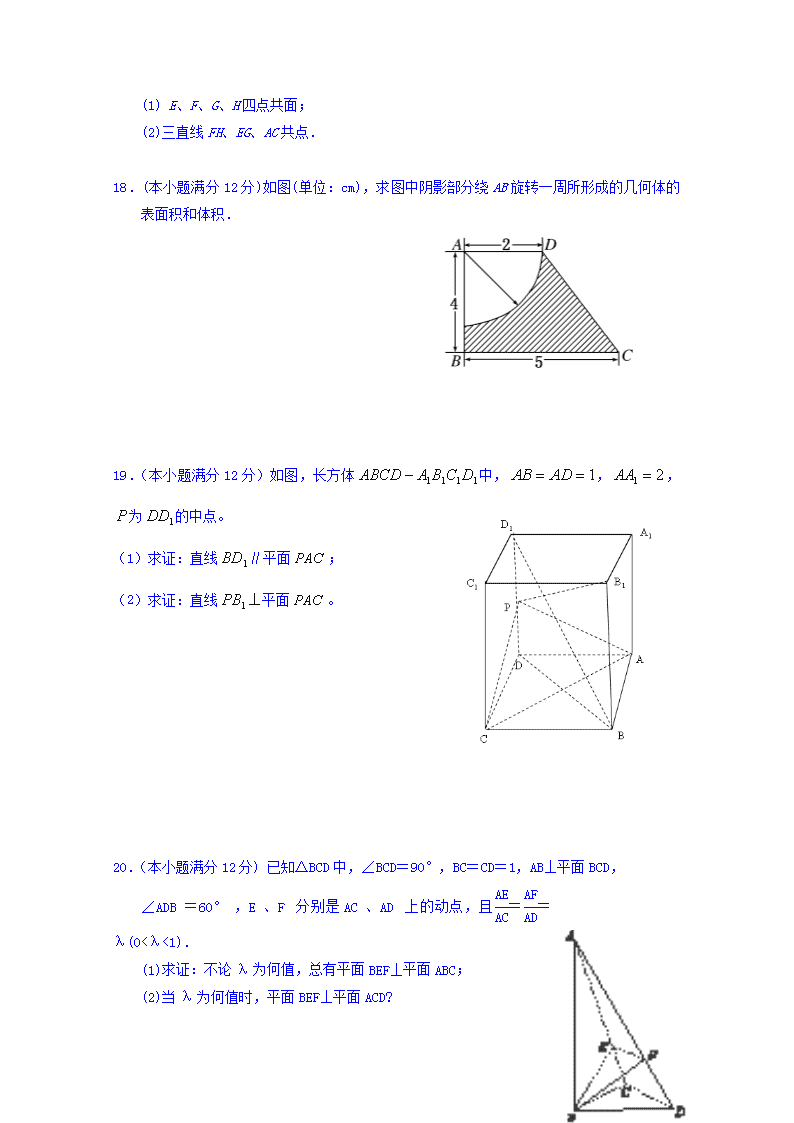
18.(本小题满分12分)如图(单位:cm),求图中阴影部分绕AB旋转一周所形成的几何体的表面积和体积.
19.(本小题满分12分)如图,长方体中,,,为的中点。
(1)求证:直线∥平面;
(2)求证:直线平面。
20.(本小题满分12分) 已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,
∠ADB=60°,E、F分别是AC、AD上的动点,且==λ(0<λ<1).
(1)求证:不论λ为何值,总有平面BEF⊥平面ABC;
(2)当λ为何值时,平面BEF⊥平面ACD?
21.(本小题满分12分)如图,在直角梯形ABCP中,CP∥AB,CP⊥CB,AB=BC=CP=2,D是CP中点,将△PAD沿AD折起,使得PD⊥面ABCD.
(1)求证:平面PAD⊥平面PCD;
(2)若E是PC的中点,求三棱锥APEB的体积.
22. (原创)(本小题满分12分)(1)已知四棱台的底面都是正方形,,侧棱求该四棱台的体积。
(2)已知三棱台的上底面的面积为,下底面的面积为,该棱台的高为.求证:该三棱台的体积
A
D
B
C
A
B
C
B
高2019级高二上期第一次月考数学(理)答案
一、选择题: ABCBA ADBCC DA
二、填空题:13、 14、 15、 16、6
三、解答题:17、证:(1)连接EF,HG.CG=BC,CH=DC
。E、F分别是AB、AD的中点
,由公理知EF,HG确定一个平面,且
(2)由(1)知,,,
,
,,
结论得证。
18、解:由题意知,所求旋转体的表面积由三部分组成:圆台下底面、侧面和一半球面.
S半球=8π,S圆台侧=35π,S圆台底=25π.故所求几何体的表面积为68π cm2.
由V圆台=×(π×22++π×52)×4=52π,
V半球=π×23×=π,所以,所求几何体的体积为
V圆台-V半球=52π-π=π(cm3).
19、解:(1)设AC和BD交于点O,连PO,由P,O分别是,BD的中点,
故PO//,⊄平面, PO⊂平面。所以直线∥平面
(2)PC2=2,PB12=3,B1C2=5,所以△PB1C是直角三角形。PC,
同理PA,PA∩PC=A,所以直线平面。
20、解:(1)证明:∵AB⊥平面BCD,∴AB⊥CD. ∵CD⊥BC且AB∩BC=B,∴CD⊥平面ABC.
又==λ(0<λ<1),∴不论λ为何值,恒有EF∥CD,∴EF⊥平面ABC.
又EF⊂平面BEF,∴不论λ为何值恒有平面BEF⊥平面ABC.
(2)由(1)知,EF⊥BE,又平面BEF⊥平面ACD,∴BE⊥平面ACD,∴BE⊥AC.
∵BC=CD=1,∠BCD=90°,∠ADB=60°,AB⊥平面BCD,
∴BD=,AB=tan60°=,∴AC==,
由AB2=AE·AC得AE=,∴λ==, 故当λ=时,
21、解:(1) 证明:∵PD⊥底面ABCD,∴PD⊥AD.又由于CP∥AB,CP⊥CB,AB=BC,
∴ABCD是正方形,∴AD⊥CD,又PD∩CD=D,故AD⊥平面PCD,
∵AD⊂平面PAD,∴平面PAD⊥平面PCD.
(2)∵AD∥BC,又BC⊂平面PBC,AD⊄平面PBC,∴AD∥平面PBC,
∴点A到平面PBC的距离即为点D到平面PBC的距离.又∵PD=DC,E是PC的中点,
∴DE⊥PC.由(1)知有AD⊥平面PCD,∴AD⊥DE.由题意得AD∥BC,故BC⊥DE.
于是,由BC∩PC=C,可得DE⊥平面PBC.∴DE=,PC=2,,下底面
又∵AD⊥平面PCD,∴AD⊥CP,∵AD∥BC,∴CP⊥BC,
∴S△PEB=S△PBC=×=,∴VAPEB=VDPEB=×DE×S△PEB=.
22、 解析:(1)易求得棱台的高为4,所以
(2)证明:延长过点S作,交平面于点,易知,则,连接,。设,
由三角形相似可知,,即,
解得,所以=