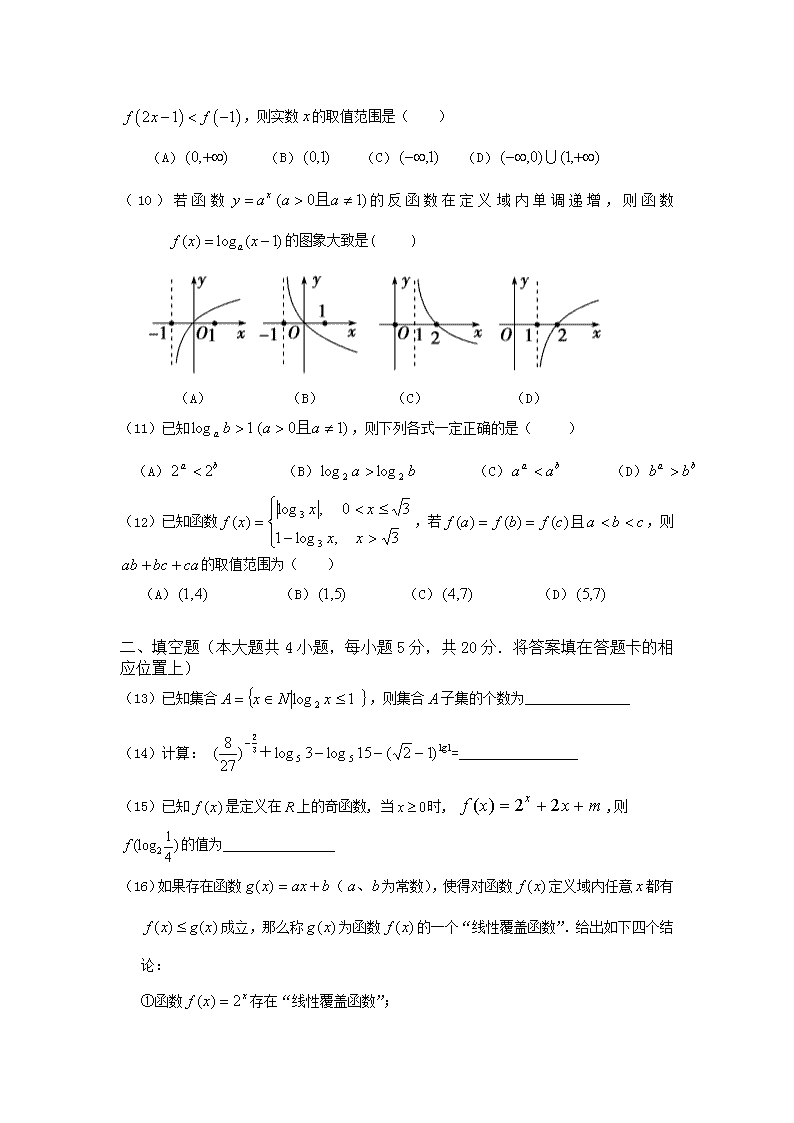2019-2020学年福建省莆田第七中学高一上学期期中复习检测数学试题2 13页

‎2019-2020学年福建省莆田第七中学高一上学期期中复习检测数学试题2‎ ‎ 考试时间：120分钟 满分：150分 一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，有且只有一项是符合题意要求的）‎ ‎（1）设全集，集合， ，则（ ）‎ ‎（A） （B） （C） （D）‎ ‎（2）函数的定义域是（ ） ‎ ‎（A） （B） （C） （D）‎ ‎（3）已知幂函数的图象过（4，2）点，则（ ）‎ ‎ （A） （B） （C） （D）‎ ‎（4）设函数 ，若，则的值为（ ）‎ ‎（A）2 （B）1 （C） （D） ‎ ‎（5）下列函数中，既是偶函数，又在上单调递增的是（ ）‎ ‎ （A） （B） （C） （D）‎ ‎（6）已知函数的图象恒过定点A，若点A也在函数的图象上，则=（ ）‎ ‎（A）0 （B）1 （C）2 （D）3‎ ‎（7）利用二分法求方程的近似解，可以取的一个区间是（ ）‎ ‎（A） （B） （C） （D）‎ ‎（8）已知，则的大小关系为（ ）‎ ‎ （A） （B） （C） （D）‎ ‎（9）已知函数是定义在上的偶函数，且在上是减函数，若 ‎，则实数的取值范围是（ ）‎ ‎ （A） （B） （C） （D）‎ ‎（10）若函数的反函数在定义域内单调递增，则函数的图象大致是( )‎ ‎ ‎ ‎ （A） （B） （C） （D）‎ ‎（11）已知，则下列各式一定正确的是（ ）‎ ‎（A） （B） （C） （D）‎ ‎（12）已知函数，若且，则的取值范围为（ ）‎ ‎（A） （B） （C） （D）‎ 二、填空题（本大题共4小题，每小题5分，共20分．将答案填在答题卡的相应位置上）‎ ‎（13）已知集合，则集合子集的个数为_______________‎ ‎（14）计算： =_________________ ‎ ‎（15）已知是定义在上的奇函数, 当时, ,则的值为________________ ‎ ‎（16）如果存在函数（为常数），使得对函数定义域内任意都有成立，那么称为函数的一个“线性覆盖函数”．给出如下四个结论：‎ ‎①函数存在“线性覆盖函数”；‎ ‎②对于给定的函数，其“线性覆盖函数”可能不存在，也可能有无数个；‎ ‎③为函数的一个“线性覆盖函数”；‎ ‎④若为函数的一个“线性覆盖函数”，则 其中所有正确结论的序号是___________‎ 三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤.‎ ‎（17）(本题满分10分)‎ 已知全集，集合,。(1)求；‎ ‎(2)若集合，且，求实数的取值范围．‎ ‎（18）（本题满分12分）‎ ‎⑴若，试求的值；⑵计算：．‎ ‎（19）（本题满分12分）‎ 已知函数是定义在上的偶函数，且当时，；‎ ‎（1）求函数在上的解析式并画出函数的图象（不要求列表描点，只要求画出草图）‎ ‎（2）写出函数的单调递增区间；‎ ‎（20）（本题满分12分）‎ 已知函数f（x）=．（1）判断函数在区间[1，+∞）上的单调性，并用定义证明你的结论．‎ ‎（2）求该函数在区间[1，4]上的最大值与最小值．‎ ‎（21）（本题满分12分）‎ 已知2x≤256，且log2x≥．（1）求x的取值范围；（2）求函数f（x）=log2（）•log2（）的最大值和最小值．‎ ‎（22）（本题满分12分）‎ 近年来，“共享单车”的出现为市民“绿色出行”提供了极大的方便，某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元，根据行业规定，每个城市至少要投资40万元，由前期市场调研可知：甲城市收益与投入（单位：万元）满足，乙城市收益与投入（单位：万元）满足，设甲城市的投入为（单位：万元），两个城市的总收益为（单位：万元）。‎ ‎（1）当甲城市投资50万元时，求此时公司总收益；‎ ‎（2）试问如何安排甲、乙两个城市的投资，才能使总收益最大？‎ ‎ 2019-2020学年上学期期中考高中一年数学 科试卷（答案卷）考号 考试时间：120分钟 满分：150分 成绩 ‎ 一、选择题:（每题 5 分，共 60 分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 二、填空题:（每小题 5 分，共 20分）‎ ‎13． 14. 15． 16． ‎ 三、解答题（本大题共6小题，共70分）‎ ‎（17）（本小题共10分）‎ 解： ‎ ‎ ‎ ‎（18）（本小题共12分）‎ 解： ‎ ‎（19）（本题满分12分）‎ 解：‎ ‎（20）（本题满分12分）‎ 解： ‎ ‎（21）（本题满分12分）‎ 解： ‎ ‎（22）（本题满分12分）‎ 解：‎ ‎……………………………………………………………装…………….…………..钉……………………….线……………………………………………………………..‎ ‎2019-2020学年上学期期中考高中一年数学科试卷（答案）‎ 一、选择题:（每题 5 分，共 60 分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B C A D D B C A B D C D 二、填空题:（每小题 5 分，共 20分）‎ ‎13． 4 14． 15． -7 16． ②③ ‎ 三、解答题（本大题共6小题，共70分）‎ ‎（17）（本小题共10分）‎ 解： (1) ‎ ‎ ‎ ‎（2）①当时，即，所以，此时 满足题意 ‎ ‎②当时，，即时，‎ 所以，解得：‎ 综上，实数a的取值范围是 ‎（18）（本小题共12分）‎ 解：⑴ ⑵ ‎ ‎（19）（本题满分12分）‎ 解：（1）设则 ‎ 所以 ‎ 又因为为奇函数，所以 ‎ 所以 即 ‎ ‎ 所以 图象略 ‎（2）由图象得函数的单调递增区间为和 ‎（20）（本题满分12分）‎ 解：任取x1，x2∈[1，+∞），且x1＜x2，‎ f（x1）﹣f（x2）==，‎ ‎∵x1﹣x2＜0，（x1+1）（x2+1）＞0，‎ 所以f（x1）﹣f（x2）＜0，即f（x1）＜f（x2），‎ 所以函数f（x）在[1，+∞）上是增函数．‎ ‎（2）由（1）知函数f（x）在[1，4]上是增函数，‎ ‎∴最大值f（4）=，最小值f（1）=．‎ ‎（21）（本题满分12分）‎ 解：（1）由2x≤256，解得：x≤8，‎ 由log2x≥，得：x≥，∴≤x≤8；‎ ‎（2）由（1）≤x≤8得：≤log2x≤3，‎ f（x）=（﹣1）（﹣2）=﹣，‎ 当=，∴x=时：f（x）min=﹣；当=3，∴x=8时：f（x）max=2．‎ ‎（22）（本题满分12分）‎ 解：（1）当时，此时甲城市投资50万元，乙城市投资70万元 ‎ 所以总收益 =43.5（万元）‎ ‎（2）由题知，甲城市投资万元，乙城市投资万元 所以 依题意得，解得 故 令，则 所以 当，即万元时，的最大值为44万元 所以当甲城市投资72万元，乙城市投资48万元时，总收益最大，且最大收益为44万元 评分细则说明：1.函数定义域没写扣1分