【数学】河北省石家庄市2020届高三五月模拟（七）试题（文）（解析版） 20页

河北省石家庄市2020届高三五月模拟（七）‎ 数学试题（文）‎ 一、选择题：在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1.已知集合，，则（ ）．‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】由，可得，得，‎ 所以.‎ 故选：C.‎ ‎2.已知，其中是虚数单位，则（ ）．‎ A. B. C. 2 D. 3‎ ‎【答案】B ‎【解析】由题意，复数，‎ 所以.‎ 故选：B.‎ ‎3.已知向量，，且与垂直，则（ ）．‎ A. 3 B. ‎2 ‎C. D. 3‎ ‎【答案】A ‎【解析】由题意，向量，，则，，‎ 因为与垂直，可得，‎ 即，解得.‎ 故选：A.‎ ‎4.若双曲线的实轴长为4，则其渐近线的方程为（ ）．‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎【解析】由双曲线的实轴长为4，可得，即，‎ 又由，所以双曲线的渐近线方程为.‎ 故选：C.‎ ‎5.用表示掷一枚质地均匀的骰子向上的点数，则方程有两个不等实根的概率为（ ）．‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】掷一枚质地均匀的骰子向上的点数的基本事件有：1，2，3，4，5，6，共6种，‎ 因为方程有两个不等实根，‎ 所以，‎ 解得，‎ 所以方程有两个不等实根的点数的基本事件有：4，5，6，共3种，‎ 所以方程有两个不等实根的概率为.‎ 故选：B ‎6.已知，则下列不等关系一定成立的是（ ）．‎ A. B. C. D. 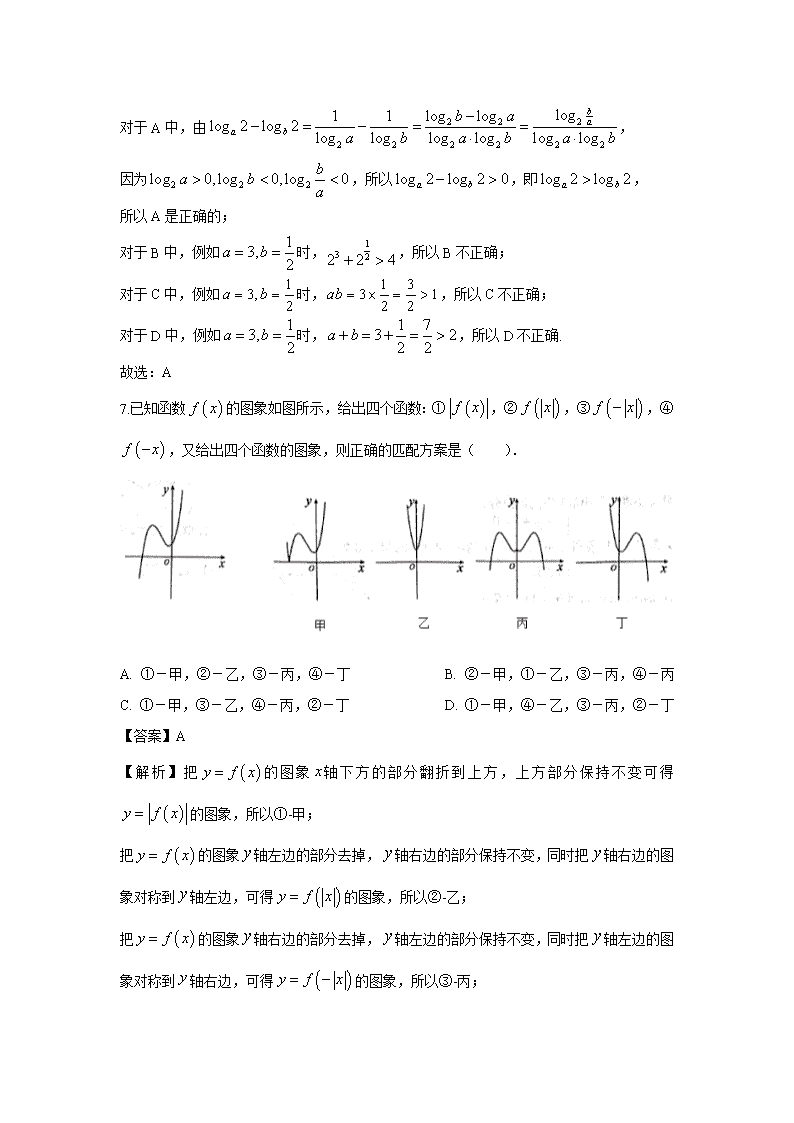‎ ‎【答案】A ‎【解析】由，可得，‎ 对于A中，由，‎ 因为，所以，即，‎ 所以A是正确的；‎ 对于B中，例如时，，所以B不正确；‎ 对于C中，例如时，，所以C不正确；‎ 对于D中，例如时，，所以D不正确.‎ 故选：A ‎7.已知函数的图象如图所示，给出四个函数：①，②，③，④，又给出四个函数的图象，则正确的匹配方案是（ ）．‎ A. ①－甲，②－乙，③－丙，④－丁 B. ②－甲，①－乙，③－丙，④－丙 C. ①－甲，③－乙，④－丙，②－丁 D. ①－甲，④－乙，③－丙，②－丁 ‎【答案】A ‎【解析】把的图象轴下方的部分翻折到上方，上方部分保持不变可得的图象，所以①-甲；‎ 把的图象轴左边的部分去掉，轴右边的部分保持不变，同时把轴右边的图象对称到轴左边，可得的图象，所以②-乙；‎ 把的图象轴右边的部分去掉，轴左边的部分保持不变，同时把轴左边的图象对称到轴右边，可得的图象，所以③-丙；‎ 作的图象关于轴的对称图象，可得的图象，所以④-丁；‎ 故选：A.‎ ‎8.已知函数，若，函数在上单调，则的最小值为（ ）．‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】由题意，函数，‎ 令，解得 则函数的对称中心的横坐标为，‎ 又因为，函数在上单调，‎ 所以，‎ 当时，，即的最小值为.‎ 故选：C.‎ ‎9.某几何体的三视图如图所示，其中网格纸上小正方形的边长为1，则该几何体的外接球的表面积为（ ）．‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】根据几何体的三视图可得：该几何体是底面为等腰直角三角形，高为的三棱锥，如图所示：‎ 设该三棱锥的外接球的球心为，则外接球的半径为，‎ 则，即，解得，‎ 所以外接球的表面积为.‎ 故选：B.‎ ‎10.若为的各位数字之和，如：，，则；记，，，…，，，则（ ）．‎ A. 2 B. ‎8 ‎C. 5 D. 11‎ ‎【答案】B ‎【解析】∵，∴，‎ ‎∵，∴，‎ ‎∵，∴，‎ ‎∵，∴，‎ ‎∵，∴，‎ ‎∵，∴，‎ ‎∴数列从第3项开始是以3为周期的循环数列，‎ ‎∵，∴.‎ 故选：B.‎ ‎11.已知椭圆，，，过点的直线与椭圆交于，，过点的直线与椭圆交于，，且满足，设和的中点分别为，，若四边形为矩形，且面积为，则该椭圆的离心率为（ ）．‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】如图，不妨设，两条直线的斜率大于零时，连结，‎ 由题意知，‎ 解得，，或，（舍）‎ ‎，，‎ 在中，因为，所以，‎ 故此时，．‎ 设，，则，‎ 两式相减得，‎ 即，即，‎ 因此离心率，所以，故选D．‎ ‎12.如图，平面四边形中，的面积是面积的3倍，数列满足，，当时，恒有，则数列的前6项和为（ ）．‎ A. 2020 B. ‎1818 ‎C. 911 D. 912‎ ‎【答案】D ‎【解析】如图，连接交于点，‎ 由，得，，‎ 设，，，‎ ‎，‎ 又与不共线，‎ 所以，则，‎ 即，‎ 所以，‎ 所以，‎ 即，‎ 所以是以2为首项，4为公比的等比数列，‎ 所以，‎ 由，，…，，‎ 累加得，‎ 所以，‎ 所以．‎ 故选：D．‎ 二、填空题：‎ ‎13.等差数列中，，则______．‎ ‎【答案】40‎ ‎【解析】由题意可知：，所以解得：.‎ 故答案为：40.‎ ‎14.已知实数，满足约束条件，则的最大值为______．‎ ‎【答案】3‎ ‎【解析】作出不等式表示的区域：‎ 作直线，平移得到，观察图象知在点处的截距取得最大值 联立，解得，‎ 故，最大值为.‎ 故答案为：3.‎ ‎15.已知长方体的底面是边长为1的正方形，侧棱，过作平面分别交棱，于点，，则四边形面积的最小值为______．‎ ‎【答案】‎ ‎【解析】由正方体对称性，设到直线的距离为，易得，故求四边形面积的最小值即求的最小值.‎ 又两直线上的点的距离最小值即为两直线间的距离最值，当分别为的中点时，连接，交于，连接.‎ 因为，故四边形为平行四边形，故.‎ 又，故平面，故，即 又，故.‎ 综上，，故为的最小值.‎ 此时 故答案为：‎ ‎16.已知，若过点的动直线与有三个不同交点，自左向右分别为，，，设线段的中点，则______，的取值范围为______．‎ ‎【答案】 (1). (2). ．‎ ‎【解析】设，，，‎ 由，得，‎ 故，为方程的两个根，所以，‎ 故点直线上，，‎ 过作的切线，设切点坐标为，‎ 则有，即，‎ 所以，‎ 所以，‎ 所以 因为，所以，解得，‎ 此时切线斜率，切线方程为．‎ 又，则点处的切线方程．‎ 切线、与直线的交点纵坐标分别为，，‎ 因为动直线与有三个不同交点，结合图形分析可得．‎ 故答案为：；.‎ 三、解答题：解答应写出必要的文字说明、证明过程或演算步骤．第17～21题为必考题，每个试题考生都必须作答．第22、23题为选考题，考生根据要求作答．‎ ‎（一）必考题 ‎17.已知的内角、、的对边分别为、、，且．‎ ‎（Ⅰ）求；‎ ‎（Ⅱ）若，，如图，为线段上一点，且，求的长．‎ 解：（Ⅰ）解法1：根据正弦定理，由得 ‎，‎ 整理得．‎ 因为，所以．‎ 解法2：由得，‎ 由余弦定理得：，‎ 整理得，．‎ 所以．‎ ‎（Ⅱ）解法1：在中，由余弦定理得：，‎ 整理得，解得或（舍），即．‎ 在中，由（1）结论可知：．‎ 由正弦定理得，所以，‎ 由（Ⅰ）结论可得出为锐角，所以，，‎ 在中，．‎ 解法2：中，由余弦定理得：，‎ 将（Ⅰ）中所求代入整理得：，解得或（舍），即．‎ 在中，由余弦定理可知：，‎ 所以，，‎ 在中，．‎ ‎18.如图，菱形与等边所在平面互相垂直，，，分别是线段，的中点．‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求点到平面的距离．‎ ‎（Ⅰ）证明：法一：如图，取线段的中点，连接，是线段的中点，‎ 则且．‎ 在菱形中为线段中点，则且．‎ 则且，故四边形为平行四边形，‎ 所以．‎ 又因为平面，平面，所以平面．‎ 法二：如图，取线段中点，连接，，‎ 在中，，‎ 因为平面，平面，所以平面．‎ 在菱形中，，‎ 因为平面，平面，所以平面．‎ 又因为，且，平面，‎ 所以平面平面．‎ 因为平面，所以平面．‎ ‎（Ⅱ）解：如图，在等边中取边中点，连接，则，‎ 因为平面平面且平面平面，‎ 所以平面，‎ 在菱形中，，是线段的中点，‎ 所以．‎ 连接，在中，，‎ 在中，，‎ 在中，．‎ 设点到平面的距离为，‎ 则，即，‎ ‎，‎ ‎，‎ 解得，所以点到平面的距离为．‎ ‎19.下表是我国大陆地区从2013年至2019年国内生产总值（GDP）近似值（单位：万亿元人民币）的数据表格：‎ 年份 ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ ‎2018‎ ‎2019‎ 年份代号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ 中国大陆地区GDP：‎ ‎（单位：万亿元人民币）‎ ‎（Ⅰ）求关于的线性回归方程（系数精确到）；‎ ‎（Ⅱ）党的十九大报告中指出：从2020年到2035年，在全面建成小康社会的基础上，再奋斗15年，基本实视社会主义现代化．若到2035年底我国人口增长为亿人，假设到2035年世界主要中等发达国家的人均国民生产总值的频率直方图如图所示．‎ 以（Ⅰ）的结论为依据，预测我国在2035年底人均国民生产总值是否可以超过假设的2035年世界主要中等发达国家的人均国民生产总值平均数的估计值．‎ 参考数据：，．‎ 参考公式：回归方程中斜率和截距的最小二乘估计公式分别为：，．‎ 解：（Ⅰ） ，，‎ ‎，‎ ‎，‎ 所以关于的线性回归方程为；‎ ‎（Ⅱ）到2035年底对应的年份代号为23，‎ 由（Ⅰ）的回归方程得，2035年我国国内生产总值约为 万亿元人民币，‎ 又，所以到2035年底我国人均国民生产总值约为万元人民币，‎ 由直方图，假设的2035年世界主要中等发达国家的人均国民生产总值平均数的估计值为：‎ ‎，‎ 又，所以以（Ⅰ）的结论为依据，可预测我国在2035年底人均国民生产总值可以超过假设的2035年世界主要中等发达国家的人均国民生产总值平均数的估计值．‎ ‎20.已知抛物线，斜率为2的直线与交于，两点，线段的中点为．‎ ‎（Ⅰ）求抛物线的方程；‎ ‎（Ⅱ）设为抛物线的焦点，，在轴两侧，且，求的面积．‎ 解：（Ⅰ）设直线的方程为，，，‎ 由，得，所以，‎ 由线段的中点为，可得，所以，‎ 所以抛物线的方程为．‎ ‎（Ⅱ）设直线的方程为，，，‎ 联立方程组，得，‎ 于是．‎ 由（Ⅰ）知，则，，‎ 由，得，‎ 将代入整理得，‎ 将代入上式，整理得，‎ 由，在轴两侧可知，解得，满足，‎ 又由，‎ 由，得，，‎ 从而，所以的面积为25．‎ ‎21.已知函数，，为自然对数的底数．‎ ‎（Ⅰ）若为单调递增函数，求实数的取值范围；‎ ‎（Ⅱ）当存在极小值时，设极小值点为，求证：．‎ 解：（Ⅰ）由题意知，‎ 由为增函数可知恒成立．‎ 设，，‎ 令得，‎ 当时，，单调递减，即单调递减；‎ 当时，，单调递增，即单调递增．‎ 故，又由为单调递增函数，则恒成立，因此，，所以，．‎ 经检验，当时，满足题意．‎ ‎（Ⅱ）由（Ⅰ）知时，．‎ 又因为，，且在上单调递减，‎ 所以存在使得，，‎ 令，，‎ 当时，，单调递增，‎ 故，‎ 又，在上单调递增，故存在使得．‎ 因此有在上单调递增，在上单调递减，在上单调递增，‎ 故，，利用 将代入消去得，‎ 函数的对称轴为，‎ 故在上单调递减，‎ 因此，即成立．‎ ‎（二）选考题：‎ ‎[选修4-4：坐标系与参数方程]‎ ‎22.在直角坐标系中，以坐标原点为极点，轴正半轴为极轴，建立极坐标系．曲线的极坐标方程为，曲线的参数方程为（为参数）．‎ ‎（Ⅰ）写出的极坐标方程；‎ ‎（Ⅱ）过原点的射线与的异于极点的交点为，，为上的一点，且，求面积的最大值．‎ 解：（Ⅰ）由曲线的参数方程（为参数）．‎ 可得曲线的普通方程为，即．‎ 将，代入上式，得．‎ 所以的极坐标方程为．‎ ‎（Ⅱ）设点的极坐标为，点的极坐标为，‎ 则，，‎ 于是的面积 当时，取得最大值．‎ 所以面积的最大值为．‎ ‎ [选修4-5：不等式选讲]‎ ‎23.已知函数的最大值为．‎ ‎（Ⅰ）求；‎ ‎（Ⅱ）已知，，实数，且．求证：．‎ 解：（Ⅰ）解法1：因为，‎ 当且仅当，即时，等号成立．‎ 所以函数的最大值等于4．‎ 解法2：，‎ 当时，的最大值等于4．‎ ‎（Ⅱ）已知且，‎ 要证，‎ 只需证．‎ 因为，所以，，，‎ 所以 ‎，‎ 故．‎