- 667.96 KB
- 2023-12-19 发布
邢台一中2017-2018学年上学期第二次月考
高二年级文科数学试题
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 正方体的内切和外接球的半径之比为( )
A. B. C. D.
【答案】D
【解析】 正方体的棱长是内切球的直径,正方体的对角线是外接球的直径,
设正方体的棱长为,内切球的半径为,外接球的半径为,
则,所以,所以,故选D.
2. 半径为的半圆卷成底面最大的圆锥,所得圆锥的高为( )
A. B. C. D.
【答案】C
【解析】易知圆锥底面半径为,所以高为,故选C.
3. 在空间直角坐标系,给出以下结论:①点关于原点的对称点的坐标为;②点关于平面对称的点的坐标是;③已知点与点,则的中点坐标是;④两点,间的距离为5.其中正确的是( )
A. ①② B. ①③ C. ②③ D. ②④
【答案】C
4. 已知向量,,则“”是“与夹角为锐角”的( )条件.
A. 必要不充分 B. 充分不必要 C. 充要 D. 既不充分也不必要
【答案】A
【解析】∵向量,
∴当x=5时,=(4,2)=2,此时两向量共线,
∴夹角为0.向量•=2x﹣2+2=2x,
若“夹角为锐角,则向量•=2x,
设与夹角为θ,则cosθ=>0,
即2x>0,解得x>0,
∴“x>0”是“夹角为锐角”的必要而不充分条件.
故选:A.
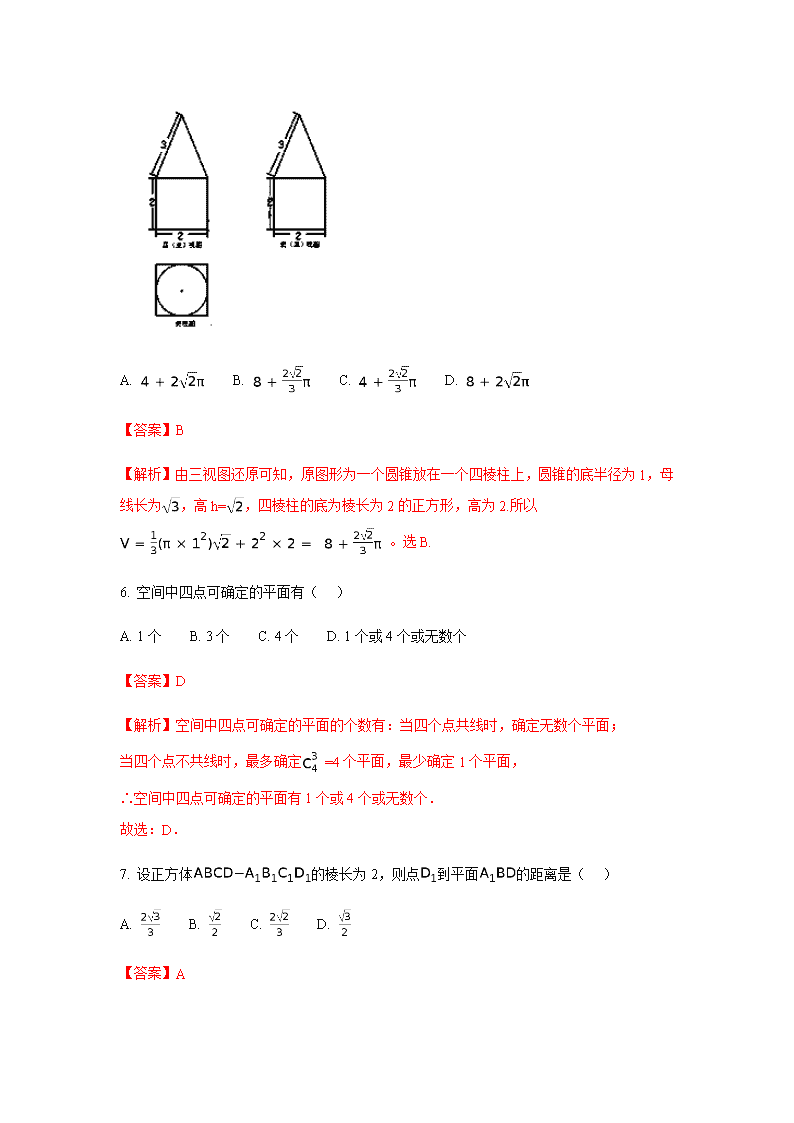
5. 某几何体的三视图如图所示,则该几何体的体积为( )
A. B. C. D.
【答案】B
【解析】由三视图还原可知,原图形为一个圆锥放在一个四棱柱上,圆锥的底半径为1,母线长为,高h=,四棱柱的底为棱长为2的正方形,高为2.所以 。选B.
6. 空间中四点可确定的平面有( )
A. 1个 B. 3个 C. 4个 D. 1个或4个或无数个
【答案】D
【解析】空间中四点可确定的平面的个数有:当四个点共线时,确定无数个平面;
当四个点不共线时,最多确定 =4个平面,最少确定1个平面,
∴空间中四点可确定的平面有1个或4个或无数个.
故选:D.
7. 设正方体的棱长为2,则点到平面的距离是( )
A. B. C. D.
【答案】A
【解析】如图, 分别以DA,DC,DD1为x,y,z轴,建立空间直角坐标系,棱长为2,,由于,可得,同理可得,所以,即面的法向量为,,
所以距离。选A.
【点睛】
点到面的距离可以用空间向量求解,求出面的法向量,这点和平面内任一点构成向量,由距离公式可求解。
8. 已知是两条不同直线,是三个不同平面,则下列正确的是( )
A. , ,则 B. 若,,则
C. 若,,则 D. 若,,则
【答案】B
【解析】试题分析:平行于同一个平面的两直线可能平行,相交或异面,故A错误;平行于同一直线的两个平面必平行,故B正确;平行于平面内的一条直线的直线和这个平面可能平行,也可能直线在平面内,故C错;垂直于同一个平面的两个平面可能平行,可能相交,故D错.综上答案选B.
考点:1.空间中的平行关系;2.空间中的垂直关系.
9. 若直线与圆有公共点,则实数取值范围是( )
A. B. C. D.
【答案】D
【解析】由题意可得,解得,选D.
【点睛】
直线与圆位置关系一般用圆心到直线距离d与半径关系来判断:
当d>r时,直线与圆相离,当d=r时,直线与圆相切,当d0,可求得m的范围。(2),(3)圆心坐标,所以圆心所在方程为y=4(x-3)2-1.
试题解析;(1) 方程表示圆的等价条件是D2+E2-4F>0,即有4(m+3)2+4(1-4m2)2-4(16m4+9)>0,
解得-