六年级下册数学教案-6《数学思考》人教版 (1) 3页

数学思考1‎ 复习内容：课本例5 ‎ 复习目标：‎ 1. 使学生学会用数学的思想方法解决问题，形成一些基本的策略，发展实践能力和创新精神。 ‎ ‎2.积累一些解决问题的经验与方法，能顺利地解决生活中复杂的数学问题。‎ ‎3．让学生进一步体验到用数学的思想解决问题的重要性，并从中体会到数学的乐趣。 ‎ 复习重点： 能用找规律、有序排列等数学的思想方法解决复杂的数学问题。‎ 复习难点： 不同问题的规律性，以及思考的顺序 ‎ 一、 谈话导入 ‎ 在解决生活问题的时候，我们要动脑思考，那么数学问题更要动脑思考，找到好方法来解决，这样的好方法就叫“策略”。板书：策略 ‎ 数学本身和生活是紧密相联的，我们今天就来解决各类数学问题。板书课题：数学思考一 ‎ 二、 探究新知 ‎ 教学例5 ‎ 1. 我们经常说到“两点一线”表示什么意思？ 那么6个点可以连接成多少条线段？ 让生连一连。 ‎ ‎2. 让生谈谈连线后的感受。 如果是8个点，10个点，甚至更多的点分别可以连接成多少条线段呢？用连线的方法方便吗？‎ ‎3. 有什么好方法解决这个问题呢？让生说一说。 怎样找规律？ 让学生说说自己的方法。 ‎ ‎4．让学生围绕思考题解决问题。课件显示思考题： ‎ ‎（１）连一连．从２个点开始连成一条线段，增加一个点，就增加＿条线段；再增加一个点，又增加了＿条线段… … ‎ ‎（２）你有什么发现？ ‎ ‎（３）６个点可以连接成多少条线段？ ８个点呢？２０个点呢？ ‎ ‎5. 学生先独立思考、解决，再在小组内交流 ‎ ‎6. 汇报，课件显示点数、增加的线段的条数、线段的总条数。‎ ‎ 教师适时提问：3个点共连接成几条线段，用算式怎么表示？（1+2=3 条） 2表示什么？ 4个点共连接成几条线段，用算式怎么表示？（1+2+3＝6 条） 3表示什 么？ „„ ‎ 7. 算一算，20个点共可连接成多少条线段？‎ 8. 如果用字母n（n≥2的自然数）表示点数，线段的条数用算式怎么表示？‎ 9. 让学生回顾解决这个问题的思维过程，以及自己的体会。感受到用数学的思想解决问题的重要性。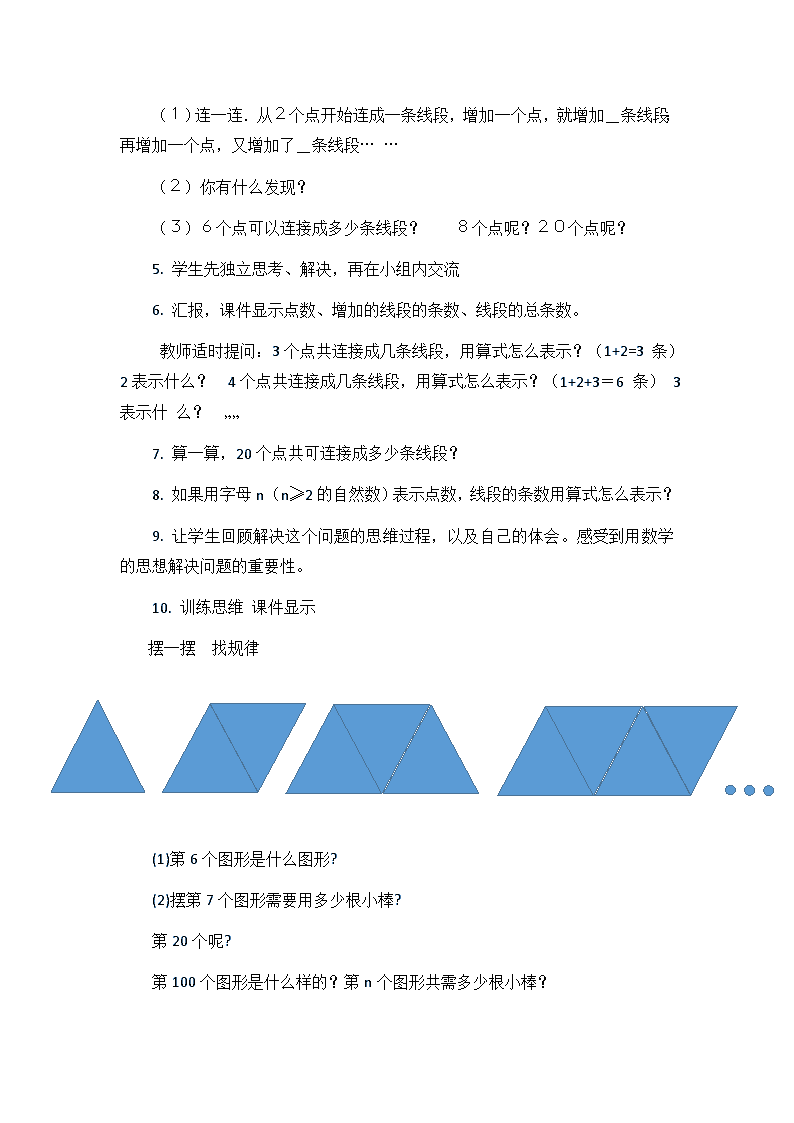 ‎ 10. 训练思维 课件显示 摆一摆 找规律 ‎(1)第6个图形是什么图形? ‎ ‎(2)摆第7个图形需要用多少根小棒? ‎ 第20个呢? ‎ 第100个图形是什么样的？第n个图形共需多少根小棒？ ‎ 小结：同学们，再碰到像这样繁杂的计数问题，你会想到怎样解决？ ‎ 板书：找规律计算，这是很好的解决问题的策略，回为它运用的是种数学的思想方法（教师板书：数学思想方法） ‎ 三．巩固练习 ‎ 四．课堂总结 ‎ 让学生说说自己的体会或收获 ‎ ‎ 教师说明：将来的学习中，我们会积累更多的解决数学问题的策略，只要我们拥有一份数学的思想，很多复杂的问题就会化难为易，迎刃而解！‎