- 345.97 KB
- 2023-12-18 发布
课时分层训练(五十八) 算法与算法框图
(对应学生用书第313页)
A组 基础达标
一、选择题
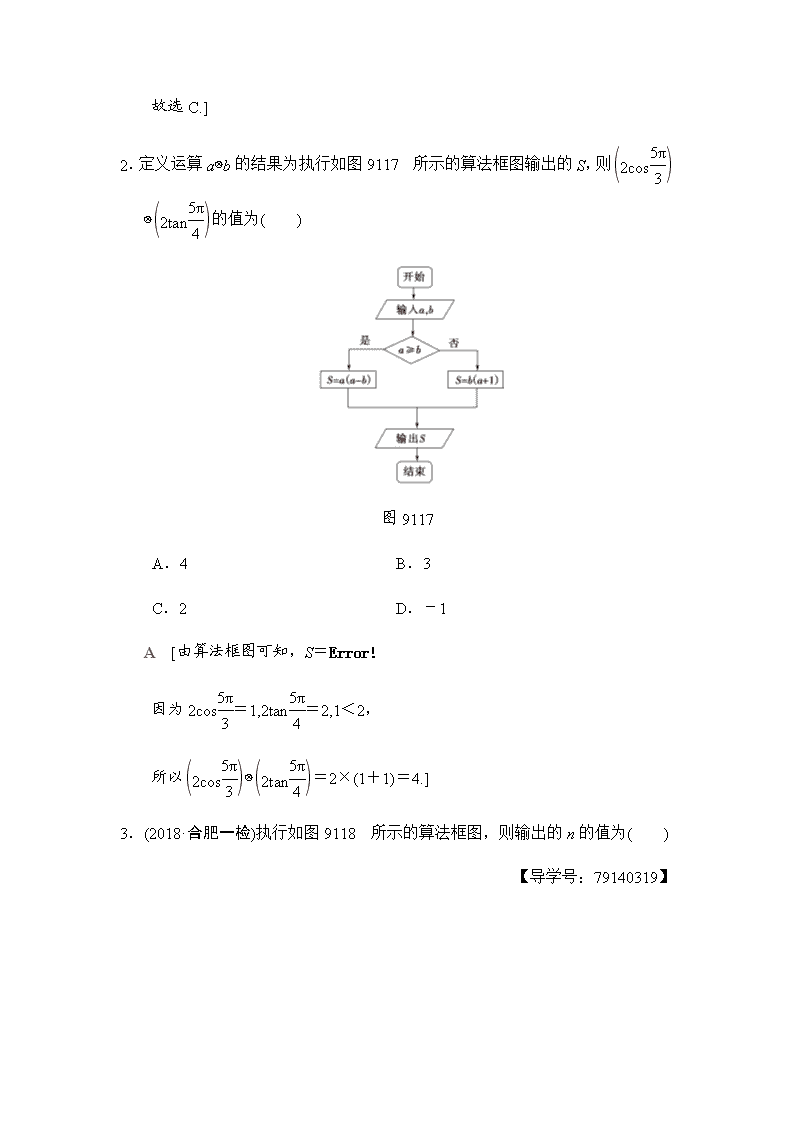
1.(2017·天津高考)阅读如图9116所示算法框图,运行相应的算法,若输入N的值为19,则输出N的值为( )
图9116
A.0 B.1
C.2 D.3
C [输入N=19,
第一次循环,19不能被3整除,N=19-1=18,18>3;
第二次循环,18能被3整除,N==6,6>3;
第三次循环,6能被3整除,N==2,2<3,满足循环条件,退出循环,输出N=2.
故选C.]
2.定义运算a⊗b的结果为执行如图9117所示的算法框图输出的S,则⊗的值为( )
图9117
A.4 B.3
C.2 D.-1
A [由算法框图可知,S=
因为2cos=1,2tan=2,1<2,
所以⊗=2×(1+1)=4.]
3.(2018·合肥一检)执行如图9118所示的算法框图,则输出的n的值为( )
【导学号:79140319】
图9118
A.3 B.4
C.5 D.6
C [第一次,k=3,n=2;第二次,k=2,n=3;第三次,k=,n=4;第四次,k=,n=5,此时,k<,循环结束,则输出的n为5,故选C.]
4.(2017·山东高考)执行如图9119所示的算法框图,当输入的x的值为4时,输出的y的值为2,则空白判断框中的条件可能为( )
图9119
A.x>3 B.x>4
C.x≤4 D.x≤5
B [输入x=4,若满足条件,则y=4+2=6,不符合题意;若不满足条件,则y=log2 4=2,符合题意,结合选项可知应填x>4.
故选B.]
5.(2017·全国卷Ⅲ)执行如图9120所示的算法框图,为使输出S的值小于91,则输入的正整数N的最小值为( )
图9120
A.5 B.4
C.3 D.2
D [假设N=2,算法执行过程如下:
t=1,M=100,S=0,
1≤2,S=0+100=100,M=-=-10,t=2,
2≤2,S=100-10=90,M=-=1,t=3,
3>2,输出S=90<91.符合题意.
所以N=2成立.显然2是最小值.
故选D.]
6.(2018·湖北调考)执行如图9121所示的算法框图,若输出的值为y=5,则满足条件的实数x的个数为( )
图9121
A.1 B.2
C.3 D.4
C [由算法框图得输出的y与输入的x的关系为y=所以当x<3时,由2x2=5得x=±;当3≤x<5时,由2x-3=5得x=4;当x≥5时,=5无解,所以满足条件的实数x的个数为3个,故选C.]
7.公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图9122是利用刘徽的“割圆术”思想设计的一个算法框图,其中n表示圆内接正多边形的边数,执行此算法输出的圆周率的近似值依次为( )
【导学号:79140320】
图9122
(参考数据:≈1.732,sin 15°≈0.258 8,sin 7.5°≈0.130 5)
A.2.598,3,3.104 8 B.2.598,3,3.105 6
C.2.578,3,3.106 9 D.2.588,3,3.110 8
B [由算法框图可得当n=6时,S=×6×sin 60°=≈2.598,输出2.598;因为6≥24不成立,执行n=2×6=12,S=×12×sin 30°=3,输出3;因为12≥24不成立,执行n=2×12=24,S=×24×sin 15°≈3.105 6,输出3.105 6,因为24≥24成立,结束运行,所以输出的圆周率的近似值依次为2.598,3,3.105 6,故选B.]
二、填空题
8.(2018·石家庄一模)算法框图如图9123所示,若输入S=1,k=1,则输出的S为________.
图9123
57 [第一次循环,得k=2,S=4;第二次循环,得k=3,S=11;第三次循环,得k=4,S=26;第四次循环,得k=5,S=57,退出循环,输出S=57.]
9.某算法框图如图9124所示,判断框内为“k≥n”,n为正整数,若输出的S
=26,则判断框内的n=________.
图9124
4 [依题意,执行题中的算法框图,进行第一次循环时,k=1+1=2,S=2×1+2=4;进行第二次循环时,k=2+1=3,S=2×4+3=11;进行第三次循环时,k=3+1=4,S=2×11+4=26.
因此当输出的S=26时,判断框内的条件n=4.]
10.执行如图9125所示的算法框图,若输入的x的值为1,则输出的n的值为________.
【导学号:79140321】
图9125
3 [由x2-4x+3≤0,解得1≤x≤3.
当x=1时,满足1≤x≤3,所以x=1+1=2,n=0+1=1;
当x=2时,满足1≤x≤3,所以x=2+1=3,n=1+1=2;
当x=3时,满足1≤x≤3,所以x=3+1=4,n=2+1=3;
当x=4时,不满足1≤x≤3,所以输出n=3.]
B组 能力提升
11.(2016·全国卷Ⅰ)执行如图9126所示的算法框图,如果输入的x=0,y=1,n=1,则输出x,y的值满足( )
图9126
A.y=2x B.y=3x
C.y=4x D.y=5x
C [输入x=0,y=1,n=1,
运行第一次,x=0,y=1,不满足x2+y2≥36;
运行第二次,x=,y=2,不满足x2+y2≥36;
运行第三次,x=,y=6,满足x2+y2≥36,
输出x=,y=6.
由于点在直线y=4x上,故选C.]
12.图9127(1)是某县参加2017年高考的学生身高条形统计图,从左到右的各小长方形表示的学生人数依次记为A1,A2,…,A10(如A2表示身高(单位:cm)在[150,155)内的学生人数).图9127(2)是统计图(1)中身高在一定范围内学生人数的一个算法框图.现要统计身高在160~180 cm(含160 cm,不含180 cm)的学生人数,则在流程图中的判断框内可填写( )
(1) (2)
图9127
A.i<6 B.i<7
C.i<8 D.i<9
C [统计身高在160~180 cm的学生人数,即求A4+A5+A6+A7的值.当4≤i≤7时,符合要求,故选C.]
13.执行如图9128所示的算法框图,输出的T的值为________.
【导学号:79140322】
图9128
[执行第一次,n=1<3,
T=1+xdx=1+x2=1+=.
执行第二次,n=2<3,
T=+x2dx=+x3=+=.
执行第三次,n=3不满足n<3,输出T=.
故输出的T的值为.]