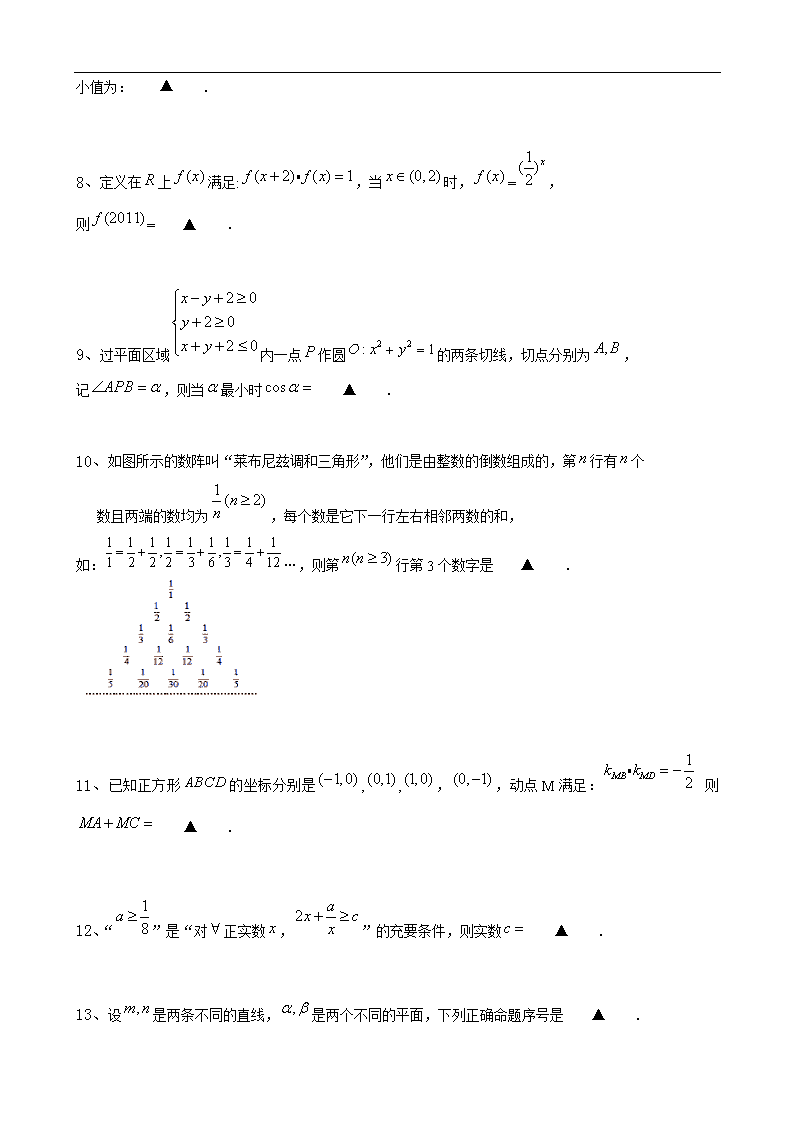- 463.00 KB
- 2023-12-17 发布
2012届南通市数学学科基地密卷(一)
一、填空题
1、执行以下语句后,打印纸上打印出的结果应是: ▲ .
While <10
End While
Print “”
2、,,若对应点在第二象限,则m的取值范围为 ▲ .
3、已知,若函数的最小正周期是2,
则 ▲ .
4、函数的定义域为,若满足①在内是单调函数,②存在,使在上的值域为,那么叫做对称函数,现有是对称函数, 那么的取值范围是 ▲ .
5、已知函数,,则的单调减区间是 ▲ .
6、在数轴上区间内,任取三个点,则它们的坐标满足不等式:
的概率为 ▲ .
7、P为抛物线上任意一点,P在轴上的射影为Q,点M(4,5),则PQ与PM
长度之和的最小值为: ▲ .
8、定义在上满足:,当时,=,
则= ▲ .
9、过平面区域内一点作圆的两条切线,切点分别为,
记,则当最小时 ▲ .
10、如图所示的数阵叫“莱布尼兹调和三角形”,他们是由整数的倒数组成的,第行有个
数且两端的数均为,每个数是它下一行左右相邻两数的和,
如:…,则第行第3个数字是 ▲ .
11、已知正方形的坐标分别是,,,,动点M满足: 则 ▲ .
12、“”是“对正实数,”的充要条件,则实数 ▲ .
13、设是两条不同的直线,是两个不同的平面,下列正确命题序号是 ▲ .
(1)若m∥,n∥,则m∥n, (2)若则
(3)若,且,则;(4)若,,则
14、已知全集,集合,则中最
大的元素是 ▲ .
二、解答题
15、已知数列满足:.
(Ⅰ)求证:使;
(Ⅱ)求的末位数字.
16、
在如图的多面体中,⊥平面,,,,
,,,是的中点.
(Ⅰ) 求证:平面;
(Ⅱ) 求证:;
(Ⅲ)求多面体的体积.
17、
已知双曲线的两焦点为,为动点,若.
(Ⅰ)求动点的轨迹方程;
(Ⅱ)若,设直线过点,且与轨迹交于、两点,直线与交于点.试问:当直线在变化时,点是否恒在一条定直线上?若是,请写出这条定直线方程,并证明你的结论;若不是,请说明理由.
18、
如图所示:一吊灯的下圆环直径为4m,圆心为O,通过细绳悬挂在天花板上,圆环呈水平状态,并且与天花板的距离为2m,在圆环上设置三个等分点A1,A2,A3。点C为上一点(不包含端点O、B),同时点C与点A1,A2,A3,B均用细绳相连接,且细绳CA1,CA2,CA3的长度相等。设细绳的总长为
(1)设∠CA1O = (rad),将y表示成θ的函数关系式;
(2)请你设计,当角θ正弦值的大小是多少时,细绳总长y最小,并指明此时 BC应为多长。
B
A1
A2
C
O
A3
19、
已知,数列有(常数),对任意的正整数,并有满足。
(1)求的值;
(2)试确定数列是不是等差数列,若是,求出其通项公式。若不是,说明理由;
(3)令,是否存在正整数M,使不等式恒成立,若存在,求出M的最小值,若不存在,说明理由。
20、
已知函数
(1)求的单调区间;
(2)若关于的不等式对一切都成立,求范围;
(3)某同学发现:总存在正实数使,试问:他的判断是否正确;
若正确,请写出的范围;不正确说明理由.
21、如图,已知三棱柱的侧棱与底面垂直,⊥AC,M是的中点,N是BC的中点,点P在直线上,且满足.
(Ⅰ)当取何值时,直线PN与平面ABC所成的角最大?
P
N
M
A
B
C
(Ⅱ)若平面PMN与平面ABC所成的二面角为,试确定点P的位置.
22、
已知二次函数f (x)=x2+mx+n对任意x∈R,都有f (-x) = f (2+x)成立,设向量
= ( sinx , 2 ) ,= (2sinx , ),= ( cos2x , 1 ),=(1,2),
(Ⅰ)求函数f (x)的单调区间;
(Ⅱ)当x∈[0,π]时,求不等式f (·)>f (·)的解集.
23、(1)(矩阵与变换)求矩阵M=的特征值及其对应的特征向量.
(2) (坐标系与参数方程)在平面直角坐标系中,椭圆C的参数方程为,其中为参数.以O为极点,轴正半轴为极轴建立极坐标系,直线l的极坐标方程为.求椭圆C上的点到直线l距离的最大值和最小值.
以下是答案
一、填空题
1、28
2、
3、-1
4、由于在上是减函数,所以关于的方程在上有两个不同实根。通过换元结合图象可得
5、
6、的实质是点在点之间,故考虑它们的排列顺序可得答案为
7、解析:焦点=,而的最小值是
8、2
9、当离圆最远时最小,此时点坐标为:记,
则,计算得=
10、
,
11、设点的坐标为,∵,∴. 整理,得(),发现动点M的轨迹方程是椭圆,其焦点恰为两点,所以
12、若则不符合题意,若则于是,亦可转化为二次函数恒成立展开讨论。
13、(3) (4)
14、3
二、解答题
15、解:⑴当
假设当
则当时,
…
其中….
所以
所以;
(2),故的末位数字是7.
16、解:(Ⅰ)证明:∵,∴.
又∵,是的中点, ∴,
∴四边形是平行四边形,∴ .
∵平面,平面,∴平面.
(Ⅱ)证明:∵平面,平面,∴,
又,平面,∴平面.
过作交于,则平面.
∵平面, ∴.
∵,∴四边形平行四边形,∴,
∴,又,
∴四边形为正方形,∴,
又平面,平面,∴⊥平面.
∵平面, ∴.
(Ⅲ) ∵平面,,∴平面,
由(2)知四边形为正方形,∴.
∴,
17、解法一:
(Ⅰ)由题意知:,又∵,∴动点必在以为焦点,
长轴长为4的椭圆,∴,又∵,.
∴椭圆的方程为.
(Ⅱ)由题意,可设直线为:.
取得,直线的方程是
直线的方程是交点为
若,由对称性可知交点为
若点在同一条直线上,则直线只能为.
②以下证明对于任意的直线与直线的交点均在直线上.
事实上,由,得即,
记,则.
设与交于点由得
设与交于点由得
,
∴,即与重合,
这说明,当变化时,点恒在定直线上.
解法二:
(Ⅰ)同解法一.
(Ⅱ)取得,直线的方程是直线的方程是交点为
取得,直线的方程是直线的方程是交点为∴若交点在同一条直线上,则直线只能为.
以下证明对于任意的直线与直线的交点均在直线上.
事实上,由,得即,
记,则.
的方程是的方程是
消去得…………………………………… ①
以下用分析法证明时,①式恒成立。
要证明①式恒成立,只需证明
即证即证……………… ②
∵∴②式恒成立.
这说明,当变化时,点恒在定直线上.
解法三:(Ⅰ)同解法一.(Ⅱ)由,得
即.
记,则.
的方程是的方程是
由得
即
.
这说明,当变化时,点恒在定直线上.
18、 (Ⅰ)解:在△COA1中,
,,
=
()
(Ⅱ),
令,则
当时,;时,,
∵在上是增函数
∴当角满足时,y最小,最小为;此时BCm
B
A1
A2
C
O
A3
19、 解:(1)由已知,得, ∴
(2)由得则,
∴,即,
于是有,并且有,
∴即,
而是正整数,则对任意都有,
∴数列是等差数列,其通项公式是。
(3)∵
∴
;
由是正整数可得,故存在最小的正整数M=3,使不等式恒成立。
20、(1)定义域
∴ ∴在递增,递减
(2)由题
∴时, 时,
时,
21、解:(1)以AB,AC,分别为轴,建立空间直角坐标系,
则,
平面ABC的一个法向量为则 (*)
于是问题转化为二次函数求最值,而当最大时,最大,所以当时,
.
(3)已知给出了平面PMN与平面ABC所成的二面角为,即可得到平面ABC的一个法向量为
,设平面PMN的一个法向量为,.
由得 ,解得.
令于是由
,
解得的延长线上,且.
22、解;(1)设f(x)图象上的两点为A(-x,y1)、B(2+x, y2),因为=1
f (-x) = f (2+x),所以y1= y2
由x的任意性得f(x)的图象关于直线x=1对称,
∴x≥1时,f(x)是增函数 ;x≤1时,f(x)是减函数。
(2)∵·=(sinx,2)·(2sinx, )=2sin2x+1≥1,
·=(cos2x,1)·(1,2)=cos2x+2≥1,
∵f(x)在是[1,+∞)上为增函数,∴f (·)>f (·)f(2sin2x+1)> f(cos2x+2)
2sin2x+1>cos2x+21-cos2x+1>cos2x+2
cos2x<02kπ+<2x<2kπ+,k∈z
kπ+<x<kπ+, k∈z ∵0≤x≤π ∴<x<
综上所述,不等式f (·)>f (·)的解集是:{ x|<x< } 。
23、解:矩阵M的特征多项式为=.
令得矩阵M的特征值为-1和3 .
当
所以矩阵M的属于特征值-1的一个特征向量为.
当
所以矩阵M的属于特征值3的一个特征向量为.
(2)解:直线l的普通方程为:,设椭圆C上的点到直线l距离为.
∴当时,,当时,.