- 346.00 KB
- 2023-12-11 发布
2016-2017学年江西省上饶市横峰中学、铅山一中高二(下)第一次联考数学试卷(理科)
一、选择题:(本题包括12小题,共60分,每小题只有一个选项符合题意)
1.过抛物线y=x2上的点的切线的倾斜角( )
A.30° B.45° C.60° D.135°
2.定积分(x+sinx)dx的值为( )
A.﹣cos1 B. +1 C.π D.
3.函数f(x)在定义域R内可导,若f(x)=f(2﹣x),且当x∈(﹣∞,1)时,(x﹣1)f'(x)<0,设则( )
A.a<b<c B.b<c<a C.a<c<b D.c<a<b
4.已知函数f(x)=ax3﹣3x2+3x,若f'(x)存在唯一的零点x0,且x0>0,则a的值是( )
A.2或1 B.0 C.1或0 D.1
5.设则等于( )
A. B. C. D.不存在
6.设函数f(x)=ex(sinx﹣cosx)(0≤x≤4π),则函数f(x)的所有极大值之和为( )
A.e4π B.eπ+e2π C.eπ﹣e3π D.eπ+e3π
7.设函数f(x)=xsinx+cosx的图象在点(t,f(t))处切线的斜率为k,则函数k=g(t)的部分图象为( )
A. B. C.
D.
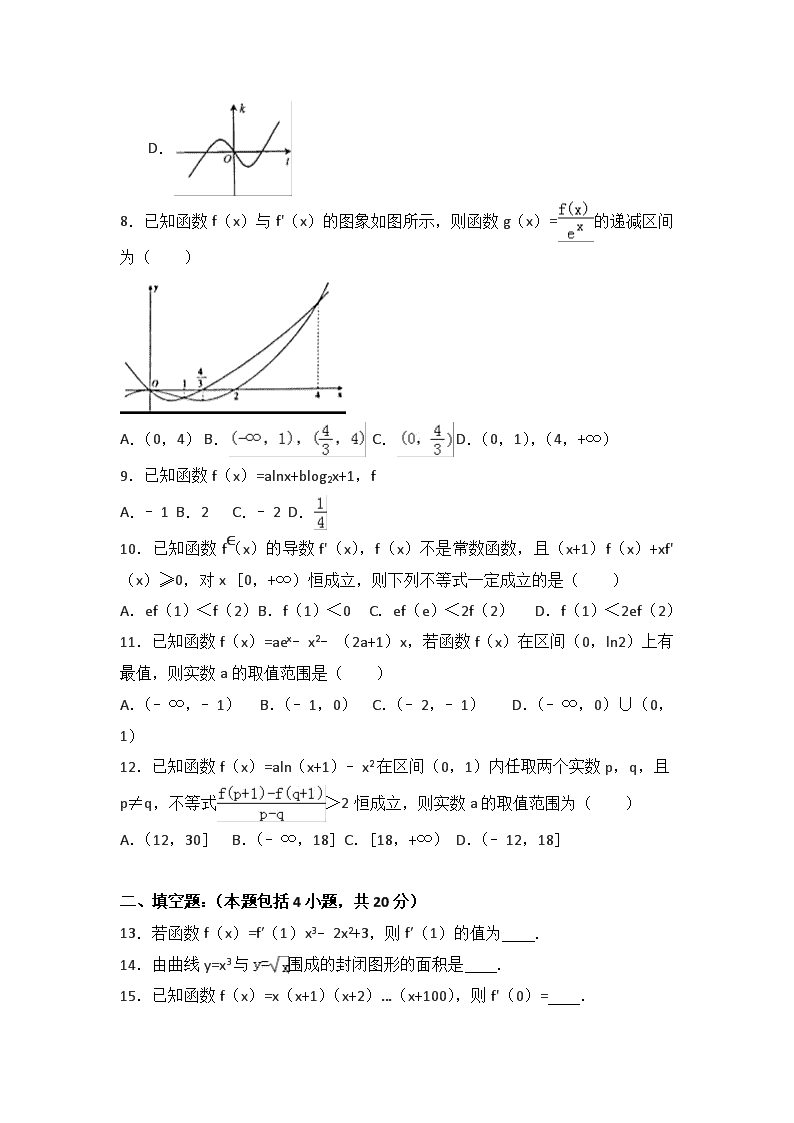
8.已知函数f(x)与f'(x)的图象如图所示,则函数g(x)=的递减区间为( )
A.(0,4) B. C. D.(0,1),(4,+∞)
9.已知函数f(x)=alnx+blog2x+1,f
A.﹣1 B.2 C.﹣2 D.
10.已知函数f(x)的导数f'(x),f(x)不是常数函数,且(x+1)f(x)+xf'(x)≥0,对x∈[0,+∞)恒成立,则下列不等式一定成立的是( )
A.ef(1)<f(2) B.f(1)<0 C.ef(e)<2f(2) D.f(1)<2ef(2)
11.已知函数f(x)=aex﹣x2﹣(2a+1)x,若函数f(x)在区间(0,ln2)上有最值,则实数a的取值范围是( )
A.(﹣∞,﹣1) B.(﹣1,0) C.(﹣2,﹣1) D.(﹣∞,0)∪(0,1)
12.已知函数f(x)=aln(x+1)﹣x2在区间(0,1)内任取两个实数p,q,且p≠q,不等式>2恒成立,则实数a的取值范围为( )
A.(12,30] B.(﹣∞,18] C.[18,+∞) D.(﹣12,18]
二、填空题:(本题包括4小题,共20分)
13.若函数f(x)=f′(1)x3﹣2x2+3,则f′(1)的值为 .
14.由曲线y=x3与围成的封闭图形的面积是 .
15.已知函数f(x)=x(x+1)(x+2)…(x+100),则f'(0)= .
16.已知f(x)=xex,g(x)=﹣(x+1)2+a,若∃x1,x2∈R,使得f(x2)≤g(x1)成立,则实数a的取值范围是 .
三、解答题:(本题包括6小题,共70分)
17.已知函数f(x)=x3﹣3x及y=f(x)上一点P(1,﹣2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于P的直线方程.
18.已知.
(1)若f(x)在x=0处的切线方程为y=x+1,求k与b的值;
(2)求.
19.已知曲线C:y2=2x﹣4.
(1)求曲线C在点A(3,)处的切线方程;
(2)过原点O作直线l与曲线C交于A,B两不同点,求线段AB的中点M的轨迹方程.
20.已知函数f(x)=alnx﹣x+1,α∈R.
(1)求f(x)的单调区间;
(2)若f(x)≤0在x∈(0,+∞)上恒成立,求所有实数a的值.
21.已知函数f(x)=xex.
(I)求f(x)的单调区间与极值;
(II)是否存在实数a使得对于任意的x1,x2∈(a,+∞),且x1<x2,恒有成立?若存在,求a的范围,若不存在,说明理由.
22.设函数y=f (x),对任意实数x,y都有f (x+y)=f (x)+f (y)+2xy.
(1)求f (0)的值;
(2)若f (1)=1,求f (2),f (3),f (4)的值;
(3)在(2)的条件下,猜想f (n)(n∈N*)的表达式并用数学归纳法证明.
2016-2017学年江西省上饶市横峰中学、铅山一中高二(下)第一次联考数学试卷(理科)
参考答案与试题解析
一、选择题:(本题包括12小题,共60分,每小题只有一个选项符合题意)
1.过抛物线y=x2上的点的切线的倾斜角( )
A.30° B.45° C.60° D.135°
【考点】利用导数研究曲线上某点切线方程.
【分析】求得函数的导数,求得切线的斜率,由直线的斜率公式,可得倾斜角.
【解答】解:y=x2的导数为y′=2x,
在点的切线的斜率为k=2×=1,
设所求切线的倾斜角为α(0°≤α<180°),
由k=tanα=1,
解得α=45°.
故选:B.
2.定积分(x+sinx)dx的值为( )
A.﹣cos1 B. +1 C.π D.
【考点】定积分.
【分析】求出被积函数的原函数,然后分别代入积分上限和积分下限后作差得答案.
【解答】解:(x+sinx)dx=(x2﹣cosx)|=(﹣cos1)﹣(0﹣1)=﹣cos1,
故选:A
3.函数f(x)在定义域R内可导,若f(x)=f(2﹣x),且当x∈(﹣∞,1)时,(x﹣1)f'(x)<0,设则( )
A.a<b<c B.b<c<a C.a<c<b D.c<a<b
【考点】利用导数研究函数的单调性.
【分析】利用导数的符号,确定函数的单调性,结合函数的对称性,判断大小.
【解答】解:因为(x)=f(2﹣x),所以函数f(x)关于x=1对称,
当x∈(﹣∞,1)时,(x﹣1)f′(x)<0,
所以f′(x)>0,所以f(x)单调递增,
而f(2)=f(0),f()=f(),
﹣1<0<,
∴f(﹣1)<f(0)=f(2)<f()=f(),
即a<c<b,
故选:C.
4.已知函数f(x)=ax3﹣3x2+3x,若f'(x)存在唯一的零点x0,且x0>0,则a的值是( )
A.2或1 B.0 C.1或0 D.1
【考点】函数零点的判定定理.
【分析】求出f(x)的导数,讨论a=0,a≠0,解方程和运用判别式为0,即可得到所求a的值.
【解答】解:函数f(x)=ax3﹣3x2+3x,
导数为f′(x)=3ax2﹣6x+3,
若f'(x)存在唯一的零点x0,且x0>0,
当a=0时,f′(x)=3﹣6x=0,解得x=>0,满足题意;
当a≠0时,△=36﹣4×3a×3=0,解得a=1,f′(x)=0,解得x=1>0.
则a的值为0或1.
故选:C.
5.设则等于( )
A. B. C. D.不存在
【考点】定积分.
【分析】根据定积分的计算法则计算即可.
【解答】解:设
则=x2dx+(2﹣x)dx=x3|+(2x﹣x2)|=+(4﹣2)﹣(2﹣)=,
故选:C
6.设函数f(x)=ex(sinx﹣cosx)(0≤x≤4π),则函数f(x)的所有极大值之和为( )
A.e4π B.eπ+e2π C.eπ﹣e3π D.eπ+e3π
【考点】利用导数研究函数的极值.
【分析】先求出其导函数,利用导函数求出其单调区间,进而找到其极大值f(2kπ+π)=e2kπ+π,即可求函数f(x)的各极大值之和.
【解答】解:∵函数f(x)=ex(sinx﹣cosx),
∴f′(x)=(ex)′(sinx﹣cosx)+ex(sinx﹣cosx)′=2exsinx,
∵x∈(2kπ,2kπ+π)时,f′(x)>0,x∈(2kπ+π,2kπ+2π)时,f′(x)<0,
∴x∈(2kπ,2kπ+π)时原函数递增,x∈(2kπ+π,2kπ+2π)时,函数f(x)=ex(sinx﹣cosx)递减,
故当x=2kπ+π时,f(x)取极大值,
其极大值为f(2kπ+π)=e2kπ+π[sin(2kπ+π)﹣cos(2kπ+π)]
=e2kπ+π×(0﹣(﹣1))
=e2kπ+π,
又0≤x≤4π,
∴函数f(x)的各极大值之和S=eπ+e3π.
故选:D.
7.设函数f(x)=xsinx+cosx的图象在点(t,f(t))处切线的斜率为k,则函数k=g(t)的部分图象为( )
A. B. C. D.
【考点】利用导数研究函数的单调性.
【分析】先对函数f(x)进行求导运算,根据在点(t,f(t))处切线的斜率为在点(t,f(t))处的导数值,可得答案.
【解答】解:∵f(x)=xsinx+cosx
∴f′(x)=(xsinx)′+(cosx)′
=x(sinx)′+(x)′sinx+(cosx)′
=xcosx+sinx﹣sinx
=xcosx
∴k=g(t)=tcost
根据y=cosx的图象可知g(t)应该为奇函数,且当x>0时g(t)>0
故选B.
8.已知函数f(x)与f'(x)的图象如图所示,则函数g(x)=的递减区间为( )
A.(0,4) B. C. D.(0,1),(4,+∞)
【考点】利用导数研究函数的单调性.
【分析】结合函数图象求出f′(x)﹣f(x)<0成立的x的范围即可.
【解答】解:结合图象:x∈(0,1)和x∈(4,+∞)时,f′(x)﹣f(x)<0,
而g′(x)=,
故g(x)在(0,1),(4,+∞)递减,
故选:D.
9.已知函数f(x)=alnx+blog2x+1,f
A.﹣1 B.2 C.﹣2 D.
【考点】函数的值.
【分析】由已知得f=alnx+blog2x+1,f=aln2017+blog22017+1=3,
∴aln2017+blog22017=2,
∴=+b+1
=﹣aln2017﹣blog22017+1=﹣1.
故选:A.
10.已知函数f(x)的导数f'(x),f(x)不是常数函数,且(x+1)f(x)+xf'(x)≥0,对x∈[0,+∞)恒成立,则下列不等式一定成立的是( )
A.ef(1)<f(2) B.f(1)<0 C.ef(e)<2f(2) D.f(1)<2ef(2)
【考点】利用导数研究函数的单调性;导数的运算.
【分析】根据条件构造函数F(x)=xexf (x),求出函数的导数,得到F′(x)=ex[(x+1)f(x)+xf′(x)]≥0对x∈[0,+∞)恒成立,得出函数F(x)=xexf (x)在[0,+∞)上单调递增,利用函数的单调性和导数之间的关系进行求解即可.
【解答】解:构造函数F(x)=xexf (x),则F′(x)=ex[(x+1)f(x)+xf′(x)],
∵(x+1)f(x)+xf'(x)≥0,
∴F′(x)≥0对x∈[0,+∞)恒成立,
∴函数F(x)=xexf (x)在[0,+∞)上单调递增,
∴F(1)<F(2),
∴f(1)<2ef(2),
故选:D.
11.已知函数f(x)=aex﹣x2﹣(2a+1)x,若函数f(x)在区间(0,ln2)上有最值,则实数a的取值范围是( )
A.(﹣∞,﹣1) B.(﹣1,0) C.(﹣2,﹣1) D.(﹣∞,0)∪(0,1)
【考点】导数在最大值、最小值问题中的应用.
【分析】f′(x)=aex﹣2x﹣(2a+1)=g(x),由函数f(x)在区间(0,ln2)上有最值⇔g(x)在区间(0,ln2)上存在零点.利用函数零点存在定理即可得出.
【解答】解:f′(x)=aex﹣2x﹣(2a+1)=g(x),
由函数f(x)在区间(0,ln2)上有最值⇔g(x)在区间(0,ln2)上单调且存在零点.
∴g(0)g(ln2)=(a﹣2a﹣1)(2a﹣2ln2﹣2a﹣1)<0,
可得a+1<0,解得a<﹣1.
此时g′(x)=aex﹣2在区间(0,ln2)上单调递减.
∴实数a的取值范围是(﹣∞,﹣1).
故选:A.
12.已知函数f(x)=aln(x+1)﹣x2在区间(0,1)内任取两个实数p,q,且p≠q,不等式>2恒成立,则实数a的取值范围为( )
A.(12,30] B.(﹣∞,18] C.[18,+∞) D.(﹣12,18]
【考点】函数恒成立问题.
【分析】依题意知,不等式>2恒成立等价转化为f′(x+1)>2恒成立,分离参数a,利用二次函数的单调性与最值即可求得实数a的取值范围.
【解答】解:∵f(x)=aln(x+1)﹣x2,
∴f(x+1)=aln[(x+1)+1]﹣(x+1)2,
∴f′(x+1)=﹣2(x+1),
∵p,q∈(0,1),且p≠q,
∴不等式>2恒成立⇔>2恒成立⇔f′(x+1)>2恒成立,
即﹣2(x+1)>2(0<x<1)恒成立,
整理得:a>2(x+2)2(0<x<1)恒成立,
∵函数y=2(x+2)2的对称轴方程为x=﹣2,∴该函数在区间(0,1)上单调递增,
∴2(x+2)2<18,
∴a≥18.
故选:C.
二、填空题:(本题包括4小题,共20分)
13.若函数f(x)=f′(1)x3﹣2x2+3,则f′(1)的值为 2 .
【考点】导数的运算.
【分析】求出函数f(x)的导数,计算f′(1)的值即可.
【解答】解:∵f(x)=f′(1)x3﹣2x2+3,
∴f′(x)=3f′(1)x2﹣4x,
∴f′(1)=3f′(1)﹣4,解得:f′(1)=2,
故答案为:2.
14.由曲线y=x3与围成的封闭图形的面积是 .
【考点】定积分在求面积中的应用.
【分析】作出两个曲线的图象,求出它们的交点,由此可得所求面积为函数y=x3与在区间[0,1]上的定积分的值,再用定积分计算公式加以运算即可得.
【解答】解:如图在同一平面直角坐标系内作出y=x3与的图象,则封闭图形的面积
.
故答案为:.
15.已知函数f(x)=x(x+1)(x+2)…(x+100),则f'(0)= 100! .
【考点】导数的运算.
【分析】根据题意,将f(x)的变形可得f(x)=x[(x+1)(x+2)…(x+100)]
,对其求导可得f′(x)=1•[(x+1)(x+2)…(x+100)]+x[(x+1)(x+2)…(x+100)]′,将x=0代入计算可得答案.
【解答】解:根据题意,f(x)=x(x+1)(x+2)…(x+100)=x[(x+1)(x+2)…(x+100)],
其导数f′(x)=(x)′[(x+1)(x+2)…(x+100)]+x[(x+1)(x+2)…(x+100)]′
=1•[(x+1)(x+2)…(x+100)]+x[(x+1)(x+2)…(x+100)]′
则f′(0)=1×2×3×4×…×100+0=100!;
故答案为:100!.
16.已知f(x)=xex,g(x)=﹣(x+1)2+a,若∃x1,x2∈R,使得f(x2)≤g(x1)成立,则实数a的取值范围是 a .
【考点】函数在某点取得极值的条件.
【分析】∃x1,x2∈R,使得f(x2)≤g(x1)成立,等价于f(x)min≤g(x)max,利用导数可求得f(x)的最小值,根据二次函数的性质可求得g(x)的最大值,代入上述不等式即可求得答案.
【解答】解:∃x1,x2∈R,使得f(x2)≤g(x1)成立,等价于f(x)min≤g(x)max,
f′(x)=ex+xex=(1+x)ex,
当x<﹣1时,f′(x)<0,f(x)递减,当x>﹣1时,f′(x)>0,f(x)递增,
所以当x=﹣1时,f(x)取得最小值f(x)min=f(﹣1)=﹣;
当x=﹣1时g(x)取得最大值为g(x)max=g(﹣1)=a,
所以﹣≤a,即实数a的取值范围是a≥.
故答案为:a≥.
三、解答题:(本题包括6小题,共70分)
17.已知函数f(x)=x3﹣3x及y=f(x)上一点P(1,﹣2),过点P作直线l.
(1)求使直线l和y=f(x)相切且以P为切点的直线方程;
(2)求使直线l和y=f(x)相切且切点异于P的直线方程.
【考点】直线的点斜式方程;导数的几何意义.
【分析】(1)由已知可得斜率函数为f′(x)=3x2﹣3,进而求出所过点切线的斜率,代入点斜式公式即可.
(2)设另一切点为(x0,y0),求出该点切线方程,再由条件计算.
【解答】解:(1)由f(x)=x3﹣3x得,f′(x)=3x2﹣3,
过点P且以P(1,﹣2)为切点的直线的斜率f′(1)=0,
∴所求直线方程为y=﹣2.
(2)设过P(1,﹣2)的直线l与y=f(x)切于另一点(x0,y0),
则f′(x0)=3x02﹣3.
又直线过(x0,y0),P(1,﹣2),
故其斜率可表示为=,
又=3x02﹣3,
即x03﹣3x0+2=3(x02﹣1)•(x0﹣1),
解得x0=1(舍)或x0=﹣,
故所求直线的斜率为k=3×(﹣1)=﹣,
∴y﹣(﹣2)=﹣(x﹣1),
即9x+4y﹣1=0.
18.已知.
(1)若f(x)在x=0处的切线方程为y=x+1,求k与b的值;
(2)求.
【考点】定积分;利用导数研究曲线上某点切线方程.
【分析】(1)根据导数的几何意义可得f(0)=1,f′(0)=1,列方程组解出即可;
(2)结合(1)中的导数可求得y=的原函数,利用微积分基本定理计算定积分.
【解答】解:(1)f′(x)==.
∵f(x)在x=0处的切线方程为y=x+1,
∴,即,
解得k=2,b=1.
(2)令=得,
解得k=﹣1,b=0,
∴()′=,
∴==﹣.
19.已知曲线C:y2=2x﹣4.
(1)求曲线C在点A(3,)处的切线方程;
(2)过原点O作直线l与曲线C交于A,B两不同点,求线段AB的中点M的轨迹方程.
【考点】轨迹方程;利用导数研究曲线上某点切线方程.
【分析】(1)y>0时,y=,求导数,可得切线的斜率,从而可求曲线C在点A(3,)处的切线方程;
(2)设l:y=kx代入y2=2x﹣4,利用韦达定理,结合中点坐标公式,即可求出线段AB的中点M的轨迹方程.
【解答】解:(1)y>0时,y=,
∴y′=,
∴x=3时,y′=,
∴曲线C在点A(3,)处的切线方程为y﹣=(x﹣3),即x﹣y﹣1=0;
(2)设l:y=kx,M(x,y),则
y=kx代入y2=2x﹣4,可得k2x2﹣2x+4=0,
∴△=4﹣16k2>0,∴
设A(x1,y1)、B(x2,y2),则x1+x2=,
∴y1+y2=
∴x=,y=,
∴y2=x(x>4).
20.已知函数f(x)=alnx﹣x+1,α∈R.
(1)求f(x)的单调区间;
(2)若f(x)≤0在x∈(0,+∞)上恒成立,求所有实数a的值.
【考点】利用导数研究函数的单调性;利用导数求闭区间上函数的最值.
【分析】(1)求出f′(x),根据当a≤0时,f′(x)>0恒成立,当a>0时,若f′(x)>0,则0<x<a,若f′(x)<0,则x>a,可得函数的单调区间;
(2)分别讨论a≤0和a>0的情况:a≤0时,发现在(0,1)上函数f(x)>0,∴f(x)≤0在区间x∈(0,+∞)上不可能恒成立;当a>0时,再次求导求出a的值
【解答】解:(1)∵f(x)=alnx﹣x+1,x>0,
∴f′(x)=﹣1=,
当a≤0时,f′(x)<0恒成立,此时f(x)在(0,+∞)上单调递减;
当a>0时,若f′(x)>0,则0<x<a,若f′(x)<0,则x>a,
故此时,f(x)在(0,a)上单调递增,在(a,+∞)上单调递减;
(2)由(1)知:当a≤0时,f(x)在(0,+∞)上为减区间,而f(1)=0,
∴在(0,1)上函数f(x)>0,
∴f(x)≤0在区间x∈(0,+∞)上不可能恒成立;
当a>0时,f(x)在(0,a)上递增,在(a,+∞)上递减,
f(x)max=f(a)=alna﹣a+1,
令g(a)=alna﹣a+1,
依题意有g(a)≤0,
而g′(a)=lna,且a>0
∴g(a)在(0,1)上递减,在(1,+∞)上递增,
∴g(a)min=g(1)=0,
故a=1,
21.已知函数f(x)=xex.
(I)求f(x)的单调区间与极值;
(II)是否存在实数a使得对于任意的x1,x2∈(a,+∞),且x1<x2,恒有成立?若存在,求a的范围,若不存在,说明理由.
【考点】利用导数研究函数的极值;函数恒成立问题;利用导数研究函数的单调性.
【分析】(I)利用函数的求导公式求出函数的导数,根据导数求函数的单调性和极值.
(II)构造函数g(x)=[f(x)﹣f(a)]/(x﹣a)=(xex﹣aea)/(x﹣a),x>a,求出函数导数,判断函数导函数的值与0的关系,根据导函数的单调性,求a的取值范围.
【解答】解:(I)由f′(x)=ex(x+1)=0,得x=﹣1;
当变化时的变化情况如下表:可知f(x)的单调递减区间为(﹣∞,﹣1),递增区间为(﹣1,+∞),
f(x)有极小值为f(﹣1)=﹣,但没有极大值.
(II)令g(x)=[f(x)﹣f(a)]/(x﹣a)=(xex﹣aea)/(x﹣a),x>a,
则[f(x2)﹣f(a)]/(x2﹣a)>[f(x1)﹣f(a)]/(x1﹣a)恒成立,
即g(x)在(a,+∞)内单调递增这只需g′(x)>0.而g′(x)=[ex(x2﹣ax﹣a)+aea]/(x﹣a)2
记h(x)=ex(x2﹣ax﹣a)+aea,
则h′(x)=ex[x2+(2﹣a)x﹣2a]=ex(x+2)(x﹣a)
故当a≥﹣2,且x>a时,h′(x)>0,h(x)在[a,+∞)上单调递增.
故h(x)>h(a)=0,从而g′(x)>0,不等式(*)恒成立
另一方面,当a<﹣2,且a<x<﹣2时,h′(x)<0,h(x)在[a,﹣2]上单调递减又h(a)=0,所以h(x)<0,
即g′(x)<0,g(x)在(a,﹣2)上单调递减.
从而存在x1x2,a<x1<x2<﹣2,使得g(x2)<g(x1)
∴a存在,其取值范围为[﹣2,+∞)
22.设函数y=f (x),对任意实数x,y都有f (x+y)=f (x)+f (y)+2xy.
(1)求f (0)的值;
(2)若f (1)=1,求f (2),f (3),f (4)的值;
(3)在(2)的条件下,猜想f (n)(n∈N*)的表达式并用数学归纳法证明.
【考点】抽象函数及其应用;数学归纳法.
【分析】(1)利用特殊值法判断即可;
(2)根据条件,逐步代入求解;
(3)猜想结论,根据数学归纳法的证明步骤证明.
【解答】解:(1)令x=y=0,得f(0+0)=f(0)+f(0)+2×0×0,得f(0)=0.…
(2)由f(1)=1,得f(2)=f(1+1)=f(1)+f(1)+2×1×1=4.
f(3)=f(2+1)=f(2)+f(1)+2×2×1=9.f(4)=f(3+1)=f(3)+f(1)+2×3×1=16.…
(3)由(2)可猜想f(n)=n2,…
用数学归纳法证明:
(i)当n=1时,f(1)=12=1显然成立.…
(ii)假设当n=k时,命题成立,即f(k)=k2,…
则当n=k+1时,f(k+1)=f(k)+f(1)+2×k×1=k2+1+2k=(k+1)2,
故当n=k+1时命题也成立,…
由(i),(ii)可得,对一切n∈N*都有f(n)=n2成立.…