- 714.00 KB
- 2023-12-09 发布
信丰中学2016-2017学年第二学期高二年级第二次月考
数学(理科)试题
命题人:何春良 审题人:王金明 2017/3/12
一、选择题(12×5′=60′)
1、某汽车启动阶段的路程函数为,则秒时,汽车的加速度是( )
A.14 B.4 C.10 D.6
2、若、均为非零向量,则是与共线的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分又不必要条件
3、用数学归纳法证明“能被3整除”的第二步中,当时,为了使用假设,应将变形为( )
A. B.
C. D.
4、函数y=x4-4x+3在区间上的最小值为( )
A.72 B.36 C.12 D.0
5、曲线在点处的切线与坐标轴所围三角形的面积为( )
A. B. C. D.
6、若抛物线的焦点与双曲线的一个焦点重合,则双曲线的离心率为( )
A. B. C. D.
7.如图,直三棱柱ABC﹣A1B1C1中,∠BAC=90°,AB=AC=2,,则AA1与平面AB1C1所成的角为( )
A. B. C. D.
8、右图是函数的导函数的图象,给出下列命题:
①是函数的极值点;
②是函数的最小值点;
③在处切线的斜率小于零;
④在区间上单调递增.
则正确命题的序号是( )
A.①② B.①④ C.②③ D.③④
9、设底为等边三角形的直棱柱的体积为V,那么其表面积最小时,底面边长为( )
A. B. C. D.
10、已知函数f(x)在定义域R内可导,若,且当时, ,设,,,则、、的大小关系为( )
A. B. C. D.
11、已知且关于的函数在上有极值,则 与的夹角的范围为( )
A. B. C. D.
12、抛物线与直线交于A,B两点,且A,B关于直线对称,则的值为( )
A. B. C. D.
二、填空题(4×5′=20′)
13、如右图,函数的图象在点P处的切线方程是,则 ________ ;
14、设方程x3-3x=k有三个不等的实根,则实数k的取值范围是________ ;
15、对于命题:如果是线段上一点,则;将它类比到平面 的情形是:若是△内一点,有;将它类比到空间的情形应该是:若是四面体内一点,则有___________________ ;
16、如图过抛物线y2=2px(p>0)的焦点的直线l依次交抛物线及其准线与点A,B,C,若|BC|=2|BF|,且|AF|=3,则抛物线的方程是________.
三、解答题(共70分)
17、(本小题10分)已知数列{an}前n项和为Sn,a1=-,且Sn++2=an(n≥2).
(1) 计算S1,S2,S 3,S4的值,猜想Sn的解析式;
(2) 用数学归纳法证明所得的结论.
18、(本小题12分)已知函数在点处取得极值.
(1)求,的值;
(2)若有极大值,求在上的最小值.
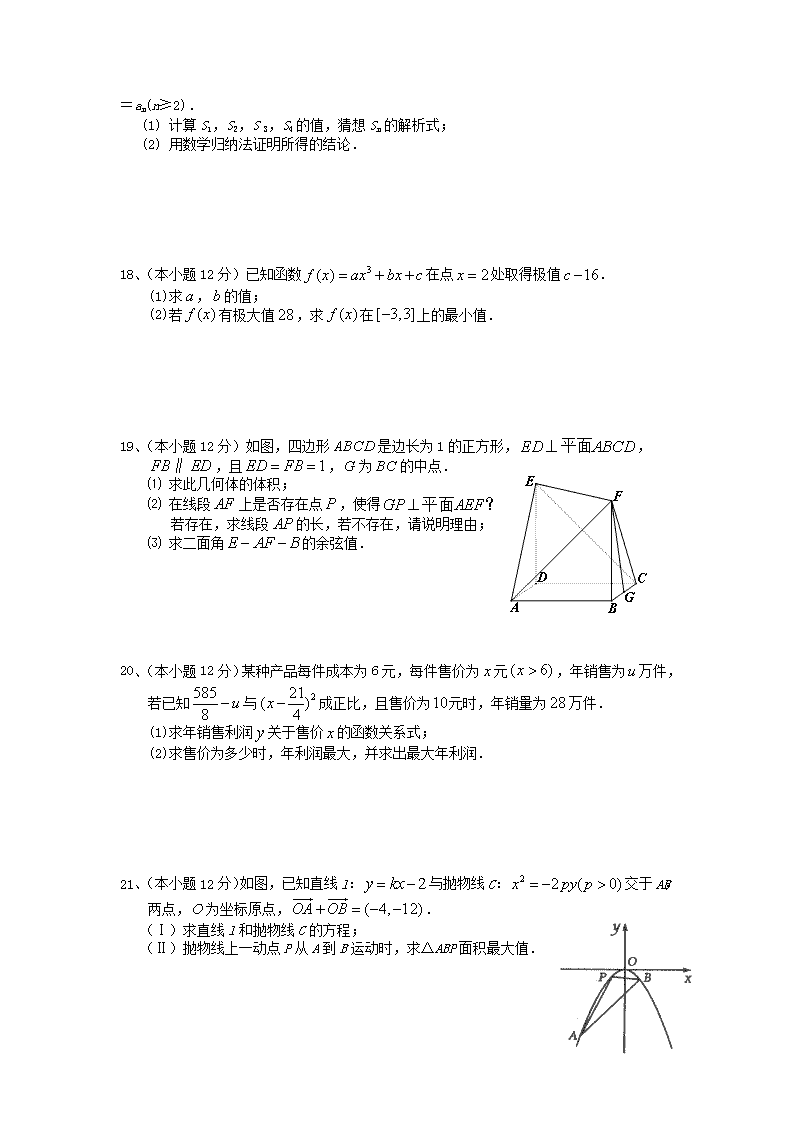
19、(本小题12分)如图,四边形是边长为1的正方形,,
,且,为的中点.
⑴ 求此几何体的体积;
⑵ 在线段上是否存在点,使得
若存在,求线段的长,若不存在,请说明理由;
⑶ 求二面角的余弦值.
20、(本小题12分)某种产品每件成本为6元,每件售价为元,年销售为万件,若已知与成正比,且售价为元时,年销量为万件.
(1)求年销售利润关于售价的函数关系式;
(2)求售价为多少时,年利润最大,并求出最大年利润.
21、(本小题12分)如图,已知直线l:与抛物线C:交于A,B两点,为坐标原点,.
(Ⅰ)求直线l和抛物线C的方程;
(Ⅱ)抛物线上一动点P从A到B运动时,求△ABP面积最大值.
22、(本小题12分)已知是函数的一个极值点。
(Ⅰ)求实数的值;
(Ⅱ)求函数的单调区间;
(Ⅲ)若直线与函数的图象有3个交点,求的取值范围.
信丰中学2016-2017学年第二学期高二年级第二次月考理科数学答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
选项
A
A
B
D
D
A
A
B
C
B
C
C
二、填空题
13、-5 14、 15、 16、
三、解答题
17、解:⑴ S1=a1=-,S2++2=S2-⇒S2=-,………………………2分
S3++2=S3-S2⇒S3=-,S4++2=S4-S3⇒S4=-.……………………4分
猜想:Sn=-(n∈N+).…………………………………………………………5分
(2)证:①当n=1时,左边=S1=a1=-,右边=-=-.
∵左边=右边,∴原等式成立.………………………………………………………6分
②当n=k时,假设Sk=-成立,由Sk+1++2=Sk+1-Sk得……………7分
=-Sk-2=-2===-,………………………8分
∴Sk+1=-=-,∴当n=k+1时,原等式也成立.…………………9分
综合(1)(2)得对一切n∈N+,Sn=-成立.……………………………………10分
18、解:(1)因为f(x)=ax3+bx+c,故f′(x)=3ax2+b.
由于f(x)在点x=2处取得极值c-16,
故有即
化简得解得……………………………………4分
(2)由 (1)知f(x)=x3-12x+c,f′(x)=3x2-12.
令f′(x)=0,得x1=-2,x2=2. ……………………………………………5分
当x∈(-∞,-2)时, f′(x)>0,故f(x)在(-∞,-2)上为增函数;
当x∈(-2,2)时,f′(x)<0,故f(x)在(-2,2)上为减函数;
当x∈(2,+∞)时,f′(x)>0,故f(x)在(2,+∞)上为增函数.…………8分
可知f(x)在x=-2处取得极大值f(-2)=16+c,在x=2处取得极小值f(2)=c-16.
由题设条件知16+c=28,解得c=12.此时f(-3)=9+c=21,f(3)=-9+c=3,
f(2)=-16+c=-4,因此f(x)在上的最小值为f(2)=-4. …………12分
20、解: (1)设-u=k2.
∵售价为10元时,年销量为28万件,
∴-28=k2,解得k=2,
∴u=-22+=-2x2+21x+18. ………………………………4分
∴y=(-2x2+21x+18)(x-6)=-2x3+33x2-108x-108.(x>6).
…………………………………………6分
(2)y′=-6x2+66x-108=-6(x2-11x+18)=-6(x-2)(x-9).………7分
令y′=0,得x=2(∵x>6,舍去)或x=9,
显然,当x∈(6,9)时,y′>0;当x∈(9,+∞)时,y′<0,………………10分
∴函数y=-2x3+33x2-108x-108在(6,9)上是增加的;在(9,+∞)上是减少的,
∴当x=9时,y取最大值,且ymax=135,
∴售价为9元时,年利润最大,最大年利润为135万元.………………………12分
21、解:(Ⅰ)由得, ………………………2分
设则
因为= ………3分
所以解得 …………………………………5分
所以直线的方程为抛物线C的方程为 …………………6分
(Ⅱ)方法1:设依题意,抛物线过P的切线与平行时,△APB面积最大,
,所以 所以………8分
此时到直线的距离 …………………9分
由得, …………………………………10分
∴△ABP的面积最大值为。………………………12分
(Ⅱ)方法2:由得,
设 ,
因为为定值,当到直线的距离最大时,△ABP的面积最大,
因为,
所以当时,max=,此时
∴△ABP的面积最大值为。
22、解:(Ⅰ)因为, 所以,
因此 . ……………3分
(Ⅱ)由(Ⅰ)知,
,
. ……………4分
当时,,……………5分
当时, . ……………6分
所以的单调增区间是,
的单调减区间是. ……………7分
(Ⅲ)由(Ⅱ)知,在内单调增加,在内单调减少,在上单调增加,且当或时,, ……………8分
所以的极大值为,极小值为. ……9分
由于,
,………10分
所以在的三个单调区间直线有的图象各有一个交点,当且仅当,
因此,的取值范围为. …………12分