高考数学复习 17-18版 第2章 第7课 二次函数与幂函数 14页

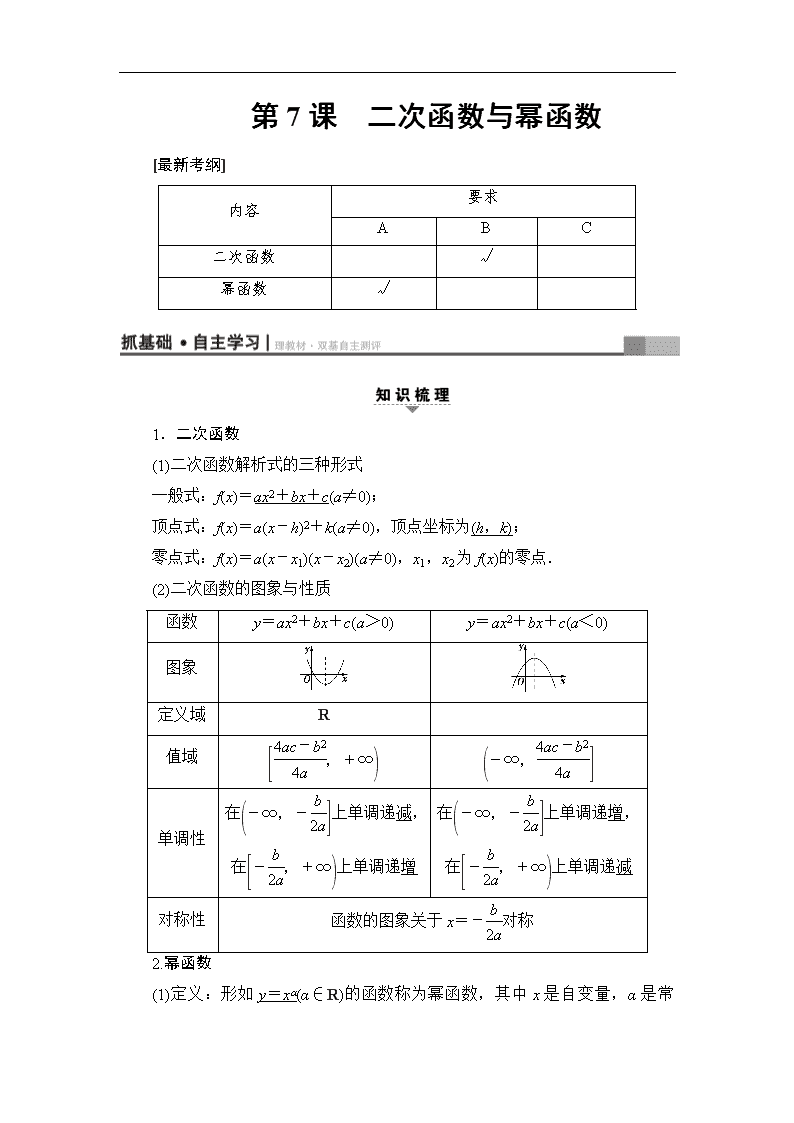
第7课 二次函数与幂函数 ‎[最新考纲]‎ 内容 要求 A B C 二次函数 ‎√‎ 幂函数 ‎√‎ ‎1．二次函数 ‎(1)二次函数解析式的三种形式 一般式：f(x)＝ax2＋bx＋c(a≠0)；‎ 顶点式：f(x)＝a(x－h)2＋k(a≠0)，顶点坐标为(h，k)；‎ 零点式：f(x)＝a(x－x1)(x－x2)(a≠0)，x1，x2为f(x)的零点．‎ ‎(2)二次函数的图象与性质 函数 y＝ax2＋bx＋c(a＞0)‎ y＝ax2＋bx＋c(a＜0)‎ 图象 定义域 R 值域 单调性 在上单调递减，‎ 在上单调递增 在上单调递增，‎ 在上单调递减 对称性 函数的图象关于x＝－对称 ‎2.幂函数 ‎(1)定义：形如y＝xα(α∈R)的函数称为幂函数，其中x是自变量，α 是常数．‎ ‎(2)五种常见幂函数的图象与性质 函数 特征 性质 y＝x y＝x2‎ y＝x3‎ y＝x y＝x－1‎ 图象 定义域 R R R ‎{x|x≥0}‎ ‎{x|x≠0}‎ 值域 R ‎{y|y≥0}‎ R ‎{y|y≥0}‎ ‎{y|y≠0}‎ 奇偶性 奇 偶 奇 非奇非偶 奇 单调性 增 ‎(－∞，0)减，‎ ‎(0，＋∞)增 增 增 ‎(－∞，0)和 ‎(0，＋∞)减 公共点 ‎(1,1)‎ ‎1．(思考辨析)判断下列结论的正误．(正确的打“√”，错误的打“×”)‎ ‎(1)二次函数y＝ax2＋bx＋c，x∈R，不可能是偶函数．(　　)‎ ‎(2)二次函数y＝ax2＋bx＋c，x∈[a，b]的最值一定是.(　　)‎ ‎(3)幂函数的图象一定经过点(1,1)和点(0,0)．(　　)‎ ‎(4)当n＞0时，幂函数y＝xn在(0，＋∞)上是增函数．(　　)‎ ‎[答案]　(1)×　(2)×　(3)×　(4)√‎ ‎2．(教材改编)已知幂函数f(x)＝xα的图象过点(4,2)，若f(m)＝3，则实数m的值为________．‎ ‎9　[由题意可知4α＝22α＝2，所以α＝.‎ 所以f(x)＝x＝，‎ 故f(m)＝＝3⇒m＝9.]‎ ‎3．已知函数f(x)＝ax2＋x＋5的图象在x轴上方，则a的取值范围是________．‎ 　[由题意知即得a＞.]‎ ‎4．二次函数f(x)＝2x2＋bx－3(b∈R)零点的个数是________．‎ ‎2　[因为判别式Δ＝b2＋24＞0，所以原二次函数有2个零点．]‎ ‎5．(2017·徐州模拟)已知函数f(x)＝x2－2x＋2的定义域和值域均为[1，b]，则b＝________.‎ ‎2　[∵f(x)＝x2－2x＋2＝(x－1)2＋1，‎ ‎∴f(x)在[1，b]上递增，‎ ‎∴即解得b＝2.]‎ 求二次函数的解析式 ‎　已知二次函数f(x)满足f(2)＝－1，f(－1)＝－1，且f(x)的最大值是8，试确定此二次函数的解析式. 【导学号：62172036】‎ ‎[解]　法一(利用一般式)：‎ 设f(x)＝ax2＋bx＋c(a≠0)．‎ 由题意得 解得 ‎∴所求二次函数为f(x)＝－4x2＋4x＋7.‎ 法二(利用顶点式)：‎ 设f(x)＝a(x－m)2＋n.‎ ‎∵f(2)＝f(－1)，‎ ‎∴抛物线的图象的对称轴为x＝＝.‎ ‎∴m＝.又根据题意函数有最大值8，∴n＝8.‎ ‎∴y＝f(x)＝a2＋8.‎ ‎∵f(2)＝－1，∴a2＋8＝－1，解得a＝－4，‎ ‎∴f(x)＝－42＋8＝－4x2＋4x＋7.‎ 法三(利用零点式)：‎ 由已知f(x)＋1＝0的两根为x1＝2，x2＝－1，‎ 故可设f(x)＋1＝a(x－2)(x＋1)，‎ 即f(x)＝ax2－ax－2a－1.‎ 又函数的最大值是8，即＝8，‎ 解得a＝－4，‎ ‎∴所求函数的解析式为f(x)＝－4x2＋4x＋7.‎ ‎[规律方法]　用待定系数法求二次函数的解析式，关键是灵活选取二次函数解析式的形式，选法如下 ‎[变式训练1]　已知二次函数f(x)的图象经过点(4,3)，它在x轴上截得的线段长为2，并且对任意x∈R，都有f(2－x)＝f(2＋x)，求f(x)的解析式．‎ ‎[解]　∵f(2－x)＝f(2＋x)对x∈R恒成立，‎ ‎∴f(x)的对称轴为x＝2.‎ 又∵f(x)的图象被x轴截得的线段长为2，‎ ‎∴f(x)＝0的两根为1和3.‎ 设f(x)的解析式为f(x)＝a(x－1)(x－3)(a≠0)．‎ 又∵f(x)的图象过点(4,3)，‎ ‎∴3a＝3，a＝1.‎ ‎∴所求f(x)的解析式为f(x)＝(x－1)(x－3)，‎ 即f(x)＝x2－4x＋3.‎ 二次函数的图象与性质 角度1　二次函数图象的识别及应用 ‎　(1)设abc＞0，则二次函数f(x)＝ax2＋bx＋c 的图象可能是________．(填序号)‎ ‎①　　　　②　　　　③　　　　④‎ 图71‎ ‎(2)已知函数f(x)＝x2＋mx－1，若对于任意x∈[m，m＋1]，都有f(x)＜0成立，则实数m的取值范围是________．‎ ‎(1)④　(2)　[(1)由①，③，④知，f(0)＝c＜0.‎ ‎∵abc＞0，∴ab＜0，∴对称轴x＝－＞0，知①，③错误，④符合要求．由②知f(0)＝c＞0，∴ab＞0，∴x＝－＜0，②错误．‎ ‎(2)作出二次函数f(x)的图象，对于任意x∈[m，m＋1]，都有f(x)＜0，则有 即解得－＜m＜0.]‎ 角度2　二次函数的最值问题 ‎　(1)若xlog52≥－1，则函数f(x)＝4x－2x＋1－3的最小值为________．‎ ‎(2)已知函数f(x)＝－x2＋2ax＋1－a在区间[0,1]上的最大值为2，求a的值. ‎ ‎【导学号：62172037】‎ ‎(1)－4　[xlog52≥－1⇒log52x≥log55－1⇒2x≥，‎ 令t＝2x，则有y＝t2－2t－3＝(t－1)2－4，‎ 当t＝1≥，即x＝0时，f(x)取得最小值－4.]‎ ‎(2)函数f(x)＝－(x－a)2＋a2－a＋1图象的对称轴为x＝a，且开口向下，分三种情况讨论如下：‎ ‎①当a≤0时，函数f(x)＝－x2＋2ax＋1－a在区间[0,1]上是减函数，‎ ‎∴f(x)max＝f(0)＝1－a，由1－a＝2，得a＝－1.‎ ‎②当0＜a≤1时，函数f(x)＝－x2＋2ax＋1－a在区间[0，a]上是增函数，在[a,1]上是减函数，‎ ‎∴f(x)max＝f(a)＝－a2＋2a2＋1－a＝a2－a＋1，‎ 由a2－a＋1＝2，解得a＝或a＝.∵0＜a≤1，∴两个值都不满足，舍去．‎ ‎③当a＞1时，函数f(x)＝－x2＋2ax＋1－a在区间[0,1]上是增函数，‎ ‎∴f(x)max＝f(1)＝－1＋2a＋1－a＝2，∴a＝2.‎ 综上可知，a＝－1或a＝2.‎ 角度3　二次函数中的恒成立问题 ‎　已知a是实数，函数f(x)＝2ax2＋2x－3在x∈[－1,1]上恒小于零，求实数a的取值范围．‎ ‎[解]　由题意知2ax2＋2x－3＜0在[－1,1]上恒成立．‎ 当x＝0时，－3＜0，适合；‎ 当x≠0时，a＜2－.‎ 因为∈(－∞，－1]∪[1，＋∞)，‎ 当x＝1时，右边取最小值，所以a＜.‎ 综上，实数a的取值范围是.‎ ‎[规律方法]　1.二次函数最值问题应抓住“三点一轴”数形结合求解，三点是指区间两个端点和中点，一轴指的是对称轴，结合配方法，用函数的单调性及分类讨论的思想即可完成．‎ ‎2．由不等式恒成立求参数的取值范围，常用分离参数法，转化为求函数最值问题，其依据是a≥f(x)⇔a≥f(x)max，a≤f(x)⇔a≤f(x)min.‎ 幂函数的图象与性质 ‎　(1)幂函数y＝f(x)的图象过点(4,2)，则幂函数y＝f(x)的图象是________．(填序号)‎ ‎①　　　　　②　　　　　③　　　　　④‎ 图72‎ ‎(2)已知幂函数f(x)＝xm2－‎2m－3(m∈N＋)的图象关于y轴对称，且在(0，＋∞)上是减函数，则m的值为________．‎ ‎(1)③　(2)1　[(1)令f(x)＝xα，则4α＝2，∴α＝，‎ ‎∴f(x)＝.‎ ‎(2)∵f(x)在(0，＋∞)上是减函数，‎ ‎∴m2－2m－3＜0，解得－1＜m＜3.‎ 又m∈N＋，∴m＝1或m＝2.‎ 由于f(x)的图象关于y轴对称．‎ ‎∴m2－2m－3的值应为偶数，‎ 又当m＝2时，m2－2m－3为奇数，‎ ‎∴m＝2舍去．因此m＝1.]‎ ‎[规律方法]　1.幂函数的形式是y＝xα(α∈R)，其中只有一个参数α，因此只需一个条件即可确定其解析式．‎ ‎2．若幂函数y＝xα(α∈R)是偶函数，则α必为偶数．当α是分数时，一般将其先化为根式，再判断．‎ ‎3．若幂函数y＝xα在(0，＋∞)上单调递增，则α＞0，若在(0，＋∞)上单调递减，则α＜0.‎ ‎[变式训练2]　(1)设a＝0.5，b＝0.9，c＝log50.3，则a，b，c的大小关系是________．‎ ‎(2)若(a＋1)＜(3－‎2a)，则实数a的取值范围是________．‎ ‎(1)c0时，图象过原点和(1,1)，在第一象限的图象上升；‎ α＜0时，图象不过原点，在第一象限的图象下降，反之也成立．‎ ‎[易错与防范]‎ ‎1．对于函数y＝ax2＋bx＋c，若是二次函数，就隐含着a≠0，当题目条件中未说明a≠0时，就要分a＝0，a≠0两种情况讨论．‎ ‎2．幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限，至于是否出现在第二、三象限内，要看函数的奇偶性；幂函数的图象最多能同时出现在两个象限内；如果幂函数图象与坐标轴相交，则交点一定是原点．‎ 课时分层训练(七)‎ A组　基础达标 ‎(建议用时：30分钟)‎ 一、填空题 ‎1．(2017·南通第一次学情检测)设幂函数f(x)＝kxα的图象经过点(4,2)，则k＋α＝________.‎ 　[由题意可知k＝1,‎4a＝2，∴α＝，∴k＋α＝1＋＝.]‎ ‎2．函数f(x)＝2x2－mx＋3，当x∈[－2，＋∞)时，f(x)是增函数，当x∈(－∞，－2]时，f(x)是减函数，则f(1)的值为________. 【导学号：62172038】‎ ‎13　[函数f(x)＝2x2－mx＋3图象的对称轴为直线x＝，由函数f(x)的增减区间可知＝－2，∴m＝－8，即f(x)＝2x2＋8x＋3，∴f(1)＝2＋8＋3＝13.]　‎ ‎3．若幂函数y＝(m2－‎3m＋3)·xm2－m－2的图象不过原点，则m的取值是________．‎ ‎1或2　[由幂函数性质可知m2－‎3m＋3＝1，∴m＝2或m＝1.又幂函数图象不过原点，∴m2－m－2≤0，即－1≤m≤2，∴m＝2或m＝1.]‎ ‎4．函数y＝－x(x≥0)的最大值为________．‎ 　[令t＝，则t≥0，所以y＝t－t2＝－2＋，结合图象(略)知，当t＝，即x＝时，ymax＝.]‎ ‎5．已知函数f(x)＝ax2－2ax＋1＋b(a＞0)．若f(x)在[2,3]上的最大值为4，最小值为1，则a＝________，b＝________. 【导学号：62172039】‎ ‎1　0　[因为函数f(x)的对称轴为x＝1，又a＞0，‎ 所以f(x)在[2,3]上单调递增，所以 即解方程得a＝1，b＝0.]‎ ‎6．已知P＝2，Q＝3，R＝3，则P，Q，R的大小关系是________．‎ P＞R＞Q　[P＝2＝3，根据函数y＝x3是R上的增函数且＞＞，‎ 得3＞3＞3，即P＞R＞Q.]‎ ‎7．对于任意实数x，函数f(x)＝(5－a)x2－6x＋a＋5恒为正值，则a的取值范围是________．‎ ‎(－4,4)　[由题意可得 解得－40，b∈R，c∈R)．‎ ‎(1)若函数f(x)的最小值是f(－1)＝0，且c＝1，‎ F(x)＝求F(2)＋F(－2)的值；‎ ‎(2)若a＝1，c＝0，且|f(x)|≤1在区间(0,1]上恒成立，试求b的取值范围．‎ ‎[解]　(1)由已知c＝1，a－b＋c＝0，‎ 且－＝－1，解得a＝1，b＝2，‎ ‎∴f(x)＝(x＋1)2.‎ ‎∴F(x)＝ ‎∴F(2)＋F(－2)＝(2＋1)2＋[－(－2＋1)2]＝8.‎ ‎(2)f(x)＝x2＋bx，原命题等价于－1≤x2＋bx≤1在(0,1]上恒成立，‎ 即b≤－x且b≥－－x在(0,1]上恒成立．‎ 又－x的最小值为0，－－x的最大值为－2，∴－2≤b≤0.‎ 故b的取值范围是[－2,0]．‎