- 737.80 KB
- 2023-12-02 发布
一、填空题(本大题共8个小题,每小题5分,共40分,则每个小题所给出的四个选项中,只有一项是符合题目要求的)
1. ,且为纯虚数,则等于
A. B. C. D.
【答案】D
【解析】∵为纯虚数,∴-a-1=0,所以a=-1,故选D
2. 已知,则“”是“”的
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
【答案】A
【解析】若“”,则,即.
所以,充分性成立;
若“”,则,有或.必要性不成立.
故“”是“”的充分不必要条件.
故选A.
3. 已知向量的夹角是,,则的值是
A. B. C. D.
【答案】A
【解析】向量的夹角是,,所以.
.
.
.
故选A.
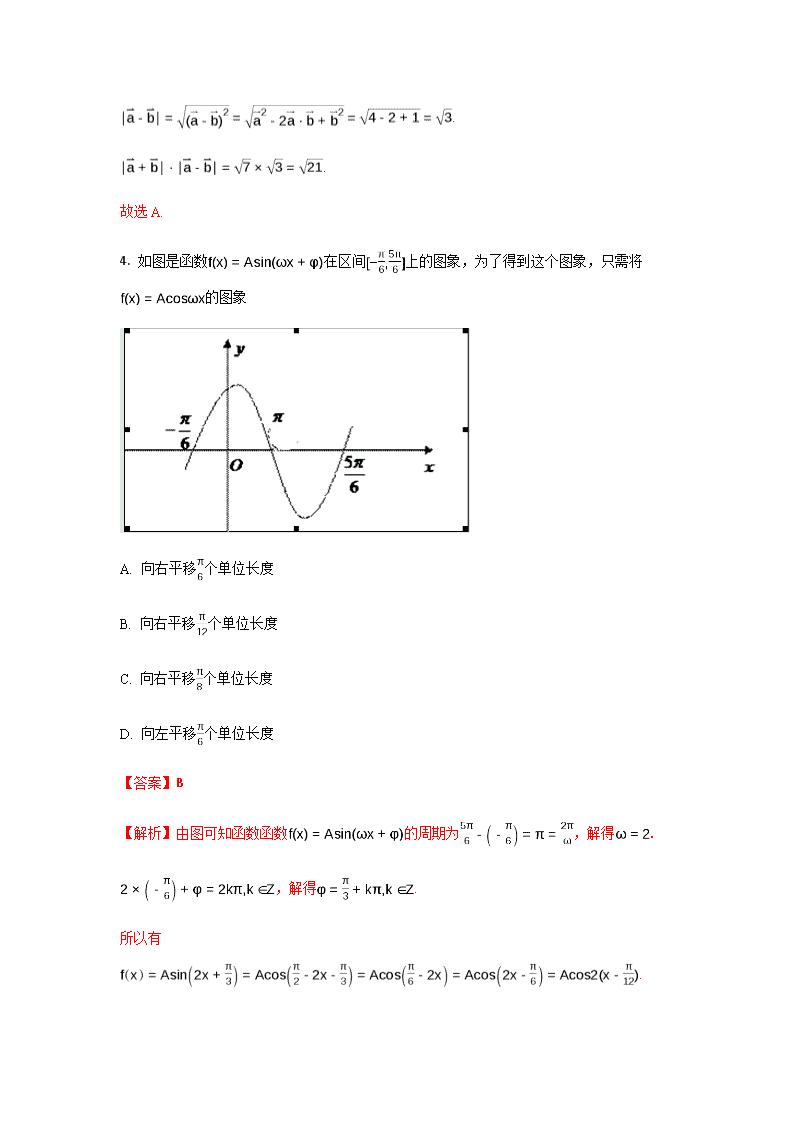
4. 如图是函数在区间上的图象,为了得到这个图象,只需将的图象
A. 向右平移个单位长度
B. 向右平移个单位长度
C. 向右平移个单位长度
D. 向左平移个单位长度
【答案】B
【解析】由图可知函数函数的周期为,解得.
,解得.
所以有.
所以只需将右平移个单位长度.
故选B.
点睛:三角函数中函数图象的平移变化是常考知识点,也是易错题型.
首项必须看清题目中是由哪个函数平移,平移后是哪个函数;
其次,在平移时,还要注意自变量x的系数是否为1,如果x有系数,需要将系数提出来求平移量,平移时遵循“左加右减”.
5. 若函数满足,且在上单调递增,则实数的最小值为
A. B. C. D.
【答案】C
知在单调递减;在单调递增.
所以.的最小值为1.
故选C.
6. 在中,角的对边分别为,且,则角的最大值为
A. B. C. D.
【答案】A
【解析】由正弦定理得,所以,因此,中有一钝角, 角必为锐角,因为 ,
所以,即角的最大值为,选A.
点睛:在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误.
7. 若函数的图象关于点对称,且在内有零点,则的最小值是
A. B. C. D.
【答案】D
【解析】函数.
图象关于点对称,所以..
当时,,令,得,.
令,无解;
当时,,令,得,.
令,解得,即零点为.
所以的最小值是10.
故选D.
8. 已知定义域为的奇函数的导函数为,当时,,若,则的大小关系正确的是
A. B. C. D.
【答案】B
【解析】定义域为R的奇函数,
设,为R上的偶函数,
当时,
所以当时,,
当时,,
即在单调递增,在单调递减.
;
;
.
因为,所以.
即 ,
故选B.
点睛:本题主要考查构造函数,常用的有:,构造xf(x);
2xf(x)+x2f′(x),构造x2f(x);
,构造;
,构造;
,构造.等等.
二、填空题(本大题共6个小题,每小题5分,共30分,请将答案填在答题卡上)
9. 若集合,则________
【答案】
【解析】集合.
.
10. 若圆经过坐标原点和点,且和直线相切,则圆的方程是_________
【答案】
【解析】设圆的圆心坐标,半径为,因为圆经过坐标原点和点,且与直线相切,所以,解得,所求圆的方程为,故答案为.
11. 已知为偶函数,则的单调递增区间为_______
【答案】
【解析】因为为偶函数,所以,所以,解得.
则函数.
令,为其对称轴.
由,解得或.
由复合函数的单调性知,单调递增区间为.
点睛:形如的函数为,的复合函数,为内层函数,为外层函数.
当内层函数单增,外层函数单增时,函数也单增;
当内层函数单增,外层函数单减时,函数也单减;
当内层函数单减,外层函数单增时,函数也单减;
当内层函数单减,外层函数单减时,函数也单增.
简称为“同增异减”.
12. 已知各项都为正数的等比数列,且满足,若存在两项,使得,则的最小是为________
【答案】
【解析】等比数列各项都为正数,则
.,则,得.;则,
则
故本题正确答案为
13. 中,分别为边的中点,且与夹角为,则______
【答案】
【解析】假设为中线与 的交点,则为三角形的重心。所以,,根据余弦定理,得。
所以
14. 已知函数,若函数有且只有三个零点,则实数的取值范围是________
【答案】
【解析】如图所示,易得,
根据题意得,
.
三、解答题(本大题共6个小题,总分80分)
15. 在中,角的对边分别为,且
(Ⅰ)求的值;
(Ⅱ)若,求的面积.
【答案】(1);(2).
试题解析:
(1)∵
∴
又∵,
∵.
则.
(2)由,得,
又∵.
则
由正弦定理知,
∴△ABC的面积为 .
16. 已知函数.
(Ⅰ)求函数的最小正周期和图象的对称中心;
(Ⅱ)求在区间上的最大值和最小值.
【答案】(1)最小正周期为:,对称中心为:;(2)最大值2,最小值.
【解析】试题分析:(1)根据二倍角的正弦与余弦及辅助角公式,将解析式化为,根据正弦函数的性质,求出最小正周期和图象的对称中心;
(2)由x的范围求出“”的范围,根据正弦函数的单调性判断出函数的单调性,再求出端点处的函数值,进行比较后得函数的最值,即求出函数的最值.
试题解析:
(1)∵
最小正周期为:,对称中心为:
(2),
当,即时函数有最大值2;
当,即时函数有最小值.
17. 某工艺厂有铜丝5万米,铁丝9万米,准备用这两种材料编制成花篮和花盆出售,已知一只花篮需要用铜丝200米,铁丝300米;编制一只花盆需要100米,铁丝300米,设该厂用所有原来编制个花篮,个花盆.
(Ⅰ)列出满足的关系式,并画出相应的平面区域;
(Ⅱ)若出售一个花篮可获利300元,出售一个花盘可获利200元,那么怎样安排花篮与花盆的编制个数,可使得所得利润最大,最大利润是多少?
【答案】(1)见解析;(2)该厂编制200个花篮,100花盆所获得利润最大,最大利润为8万元.
【解析】试题分析:(1)列出x、y满足的关系式为,画出不等式组所表示的平面区域即可.
(2)设该厂所得利润为z元,写出目标函数,利用目标函数的几何意义,求解目标函数z=300x+200y,所获得利润.
试题解析:
(1)由已知x、y满足的关系式为等价于
该二元一次不等式组所表示的平面区域如图中的阴影部分.
(2)设该厂所得利润为z元,则目标函数为z=300x+200y
将z=300x+200y变形为,这是斜率为,在y轴上截距为、随z变化的一族平行直线.
又因为x、y满足约束条件,所以由图可知,当直线经过可行域上的点M时,截距最大,即z最大.
解方程组得点M的坐标为(200,100)且恰为整点,即x=200,y=100.
所以,.
答:该厂编制200个花篮,100花盆所获得利润最大,最大利润为8万元.
点睛:线性规划的实质是把代数问题几何化,即数形结合的思想.需要注意的是:一、准确无误地作出可行域;二、画标准函数所对应的直线时,要注意与约束条件中的直线的斜率进行比较,避免出错;三、一般情况下,目标函数的最大或最小会在可行域的端点或边界上取得.
18. 已知各项均不为零的数列的前项和,且满足,数列满足.
(Ⅰ)求数列,的通项公式;
(Ⅱ)设,求数列的前项和.
【答案】(1),;(2).
【解析】试题分析:(1)由,求出,当,求出.利用,,判断数列是以2为首项,以2为公比的等比数列,然后求解;
(2)由可以利用错位相减来求和.
试题解析:
(1)
当时,,综上.
由 ,所以是以2位公比,2为首项的等比数列,所以,则.
(2),……①
……②
①-②整理得.
点睛:用错位相减法求和应注意的问题(1)要善于识别题目类型,特别是等比数列公比为负数的情形;(2)在写出“Sn”与“qSn”的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“Sn-qSn”的表达式;(3)在应用错位相减法求和时,若等比数列的公比为参数,应分公比等于1和不等于1两种情况求解.
19. 已知数列的前项和为,且满足.
(Ⅰ)求数列的通项公式;
(Ⅱ)设,求数列的前项和.
【答案】(1);(2).
【解析】试题分析:(Ⅰ)由 ,求出,,能求出数列的通项公式.
(Ⅱ)由(Ⅰ)知:,由此利用分组求和法和裂项求和法能求出数列的前n项和.
试题解析:
(1)
,当时,,所以
(2)
当为偶数时,
当为奇数时,
综上
20. 已知函数.
(Ⅰ)当时,求曲线在点处的切线方程;
(Ⅱ)当时,若在区间上的最小值为,求的取值范围;
(Ⅲ)若对任意,有恒成立,求的取值范围.
【答案】(1);(2);(3).
【解析】试题分析:(Ⅰ)把a=1代入函数解析式,求导后求出f′(1),同时求出f(1),由点斜式写出切线方程;
(Ⅱ)求出函数的定义域,求出原函数的导函数,进一步求出导函数的零点,分和三种情况讨论三种情况讨论原函数的单调性,由f(x)在区间[1,e]上的最小值为-2求解的取值范围;
(Ⅲ)构造辅助函数g(x)=f(x)+2x,问题转化为函数g(x)在(0,+∞)上单调递增,求解的范围.把函数g(x)求导后分 =0和≠0讨论,≠0时借助于二次函数过定点及对称轴列式求解.
试题解析:
(1)由,则
,所以切线方程为
(2)
令
当时,在上单调递增,
当时,在上单调递减,
(舍)
当时,在上单调递减, 在上单调递增,(舍)
综上,
(3)令
令,只要在上单调递增即可.
在上恒成立.
在上恒成立.
当时,恒成立;
当时,原不等式
当时,原不等式,左边无最大值,不合题意(舍)
综上,.
点睛:本题考查学生会利用导数求曲线上过某点切线方程的斜率,会利用导数研究函数的单调区间以及根据函数的增减性得到函数的最值.掌握不等式恒成立时所取的条件.考查了数学转化思想方法及分类讨论的数学数学思想方法,是难题.