【数学】2018届一轮复习人教A版直接证明与间接证明教案 8页

高三 一轮复习 6.6直接证明与间接证明 ‎【教学目标】‎ ‎1.了解直接证明的两种基本方法——分析法和综合法；了解分析法和综合法的思考过程和特点．‎ ‎2.了解反证法的思考过程和特点.‎ ‎【重点难点】‎ ‎ 1.教学重点 了解分析法、综合法及反证法的思考过程 ‎2.教学难点学会对知识进行整理达到系统化，提高分析问题和解决问题的能力；‎ ‎【教学策略与方法】‎ 自主学习、小组讨论法、师生互动法 ‎【教学过程】‎ 教学流程 教师活动 学生活动 设计意图 考纲传真 　1.了解直接证明的两种基本方法——分析法和综合法；了解分析法和综合法的思考过程和特点．　2.了解反证法的思考过程和特点.‎ 真题再现;‎ ‎1.(2014·山东，4)用反证法证明命题“设a，b为实数 则方程x3＋ax＋b＝0至少有一个实根”时，要做的假 设是(　　)‎ A.方程x3＋ax＋b＝0没有实根 B.方程x3＋ax＋b＝0至多有一个实根 C.方程x3＋ax＋b＝0至多有两个实根 D.方程x3＋ax＋b＝0恰好有两个实根 解析　至少有一个实根的否定是没有实根，故要做的假设是“方程x3＋ax＋b＝0没有实根”.答案　A ‎2.(2012·福建，17)某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数 ‎①sin213°＋cos217°－sin 13°cos 17°；‎ ‎②sin215°＋cos215°－sin 15°cos 15°；‎ ‎③sin218°＋cos212°－sin 18°cos 12°；‎ ‎④sin2(－18°)＋cos248°－sin(－18°)cos 48°；‎ ‎⑤sin2(－25°)＋cos255°－sin(－25°)cos 55°.‎ ‎(1)试从上述五个式子中选择一个，求出这个常数；‎ ‎。‎ 学生通过对高考真题的解决，发现自己对知识的掌握情况。‎ ‎ ‎ ‎ ‎ 通过对考纲的解读和分析。让学生明确考试要求，做到有的放矢 ‎(2)根据(1)的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论.‎ 解　(1)选择②式，计算如下sin215°＋cos215°－sin 15°cos 15°＝1－sin 30°＝1－＝.‎ ‎(2)三角恒等式为sin2α＋cos2(30°－α)－sin αcos(30°－α)＝.‎ 证明如下sin2α＋cos2(30°－α)－sin αcos(30°－α)‎ ‎＝sin2α＋(cos 30°cos α＋sin 30°sin α)2－sin α(cos 30°cos α＋sin 30°sin α)＝sin2α＋cos2α＋sin αcos α＋sin2α－sin αcos α－sin2α ‎＝sin2α＋ cos2α＝.‎ ‎3．(2013·江苏卷)已知a≥b>0，求证2a3－b3≥2ab2－a2b.‎ 证明2a3－b3－(2ab2－a2b)＝2a(a2－b2)＋b(a2－b2)‎ ‎＝(a2－b2)(2a＋b)＝(a－b)(a＋b)(2a＋b)．‎ 因为a≥b>0，所以a－b≥0，a＋b>0,2a＋b>0，‎ 从而(a－b)(a＋b)(2a＋b)≥0，‎ 即2a3－b3≥2ab2－a2b.‎ 知识梳理 知识点1　直接证明 内容 综合法 分析法 定义 利用已知条件和某些数学定义、公理、定理等，经过一系列的推理论证，最后推导出所要证明的结论成立的证明方法 从要证明的结论出发，逐步寻求使它成立的充分条件，直到最后，把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止的证明方法 思维特点 由因导果(顺推证法)‎ 执果索因(逆推证法)‎ →→‎ →…→‎ →→‎ →…→‎ 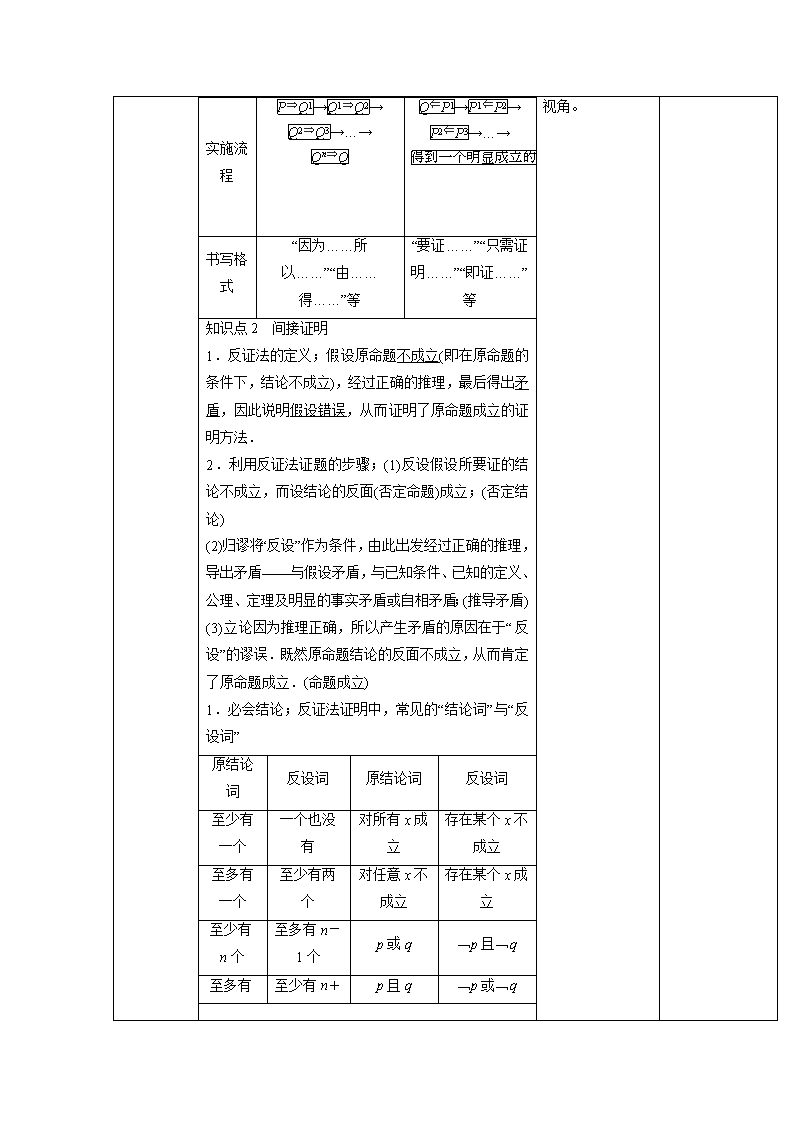实施流程 书写格式 ‎“因为……所以……”“由……得……”等 ‎“要证……”“只需证明……”“即证……”等 知识点2　间接证明 ‎1．反证法的定义；假设原命题不成立(即在原命题的条件下，结论不成立)，经过正确的推理，最后得出矛盾，因此说明假设错误，从而证明了原命题成立的证明方法．‎ ‎2．利用反证法证题的步骤；(1)反设假设所要证的结论不成立，而设结论的反面(否定命题)成立；(否定结论)‎ ‎(2)归谬将“反设”作为条件，由此出发经过正确的推理，导出矛盾——与假设矛盾，与已知条件、已知的定义、公理、定理及明显的事实矛盾或自相矛盾；(推导矛盾)‎ ‎(3)立论因为推理正确，所以产生矛盾的原因在于“反设”的谬误．既然原命题结论的反面不成立，从而肯定了原命题成立．(命题成立)‎ ‎1．必会结论；反证法证明中，常见的“结论词”与“反设词”‎ 原结论词 反设词 原结论词 反设词 至少有一个 一个也没有 对所有x成立 存在某个x不成立 至多有一个 至少有两个 对任意x不成立 存在某个x成立 至少有n个 至多有n－1个 p或q ‎﹁p且﹁q 至多有 至少有n＋‎ p且q ‎﹁p或﹁q 学生通过对高考真题的解决，感受高考题的考察视角。‎ 环节二 n个 ‎1个 ‎2.必知联系；分析法与综合法相辅相成，对较复杂的问题，常常先从结论进行分析，寻求结论与条件、基础知识之间的关系，找到解决问题的思路，再运用综合法证明，或者在证明时将两种方法交叉使用．‎ 考点分项突破 考点一综合法 ‎1.(2015·安徽高考)设n∈N*，xn是曲线y＝x2n＋2＋1在点(1,2)处的切线与x轴交点的横坐标．‎ ‎(1)求数列{xn}的通项公式；‎ ‎(2)记Tn＝xx…x，证明Tn≥.‎ ‎【解】　(1)y′＝(x2n＋2＋1)′＝(2n＋2)x2n＋1，曲线y＝x2n＋2＋1在点(1,2)处的切线斜率为2n＋2，从而切线方程为y－2＝(2n＋2)(x－1)．令y＝0，解得切线与x轴交点的横坐标xn＝1－＝，所以数列{xn}的 通项公式xn＝.‎ ‎(2)证明由题设和(1)中的计算结果知，‎ Tn＝xx…x＝22…2.‎ 当n＝1时，T1＝.当n≥2时，因为x＝2＝>＝＝，‎ 所以Tn>2×××…×＝.‎ 综上可得，对任意的n∈N*，均有Tn≥.‎ 跟踪训练 1.(2015·北京高考)设函数f(x)＝－kln x，k>0.‎ ‎(1)求f(x)的单调区间和极值；‎ ‎(2)证明若f(x)存在零点，则f(x)在区间(1，]上仅有一个零点．‎ ‎ 教师引导学生及时总结，以帮助学生形成完整的认知结构。‎ ‎【解】　(1)由f(x)＝－kln x(k>0)，得x>0且f′(x)＝x－＝.由f′(x)＝0，解得x＝(负值舍去)．‎ f(x)与f′(x)在区间(0，＋∞)上的情况如下 x ‎(0，)‎ ‎(，＋∞)‎ f′(x)‎ ‎－‎ ‎0‎ ‎＋‎ f(x)‎   所以，f(x)的单调递减区间是(0，)，单调递增区间是(，＋∞)．f(x)在x＝处取得极小值f()＝.‎ ‎(2)证明由(1)知，f(x)在区间(0，＋∞)上的最小值为f()＝.因为f(x)存在零点，所以≤0，从而k≥e.当k＝e时，f(x)在区间(1，)上单调递减，且f()＝0，所以x＝是f(x)在区间(1，]上的唯一零点．当k>e时，f(x)在区间(1，)上单调递减，且f(1)＝>0，f()＝<0，‎ 所以f(x)在区间(1，]上仅有一个零点．‎ 综上可知，若f(x)存在零点，则 f(x)在区间(1，]上仅有一个零点．‎ 归纳综合法证题的思路 考点二 分析法 引导学生通过对基础知识的逐点扫描，来澄清概念，加强理解。从而为后面的练习奠定基础.‎ 由常见问题的解决和总结，使学生形成解题模块，提高模式识别能力和解题效率。‎ 教师引导学生及时总结，以帮助学生形成完整的认知结构。‎ ‎1.　已知a>0，求证－≥a＋－2.‎ ‎【证明】　要证－≥a＋－2，‎ 只需证＋2≥a＋＋.‎ ‎∵a>0，故只需证2≥2，‎ 即a2＋＋4＋4≥a2＋2＋＋2＋2，从而只需证2≥，‎ 只需证4≥2，即a2＋≥2，而上述不等式显然成立，故原不等式成立．‎ 跟踪训练 ‎ ‎1.△ABC的三个内角A，B，C成等差数列，A，B，C的对边分别为a，b，c.‎ 求证＋＝.‎ ‎【证明】　要证＋＝，‎ 即证＋＝3，也就是＋＝1，‎ 只需证c(b＋c)＋a(a＋b)＝(a＋b)(b＋c)，‎ 需证c2＋a2＝ac＋b2，又△ABC三内角A，B，C成等差数列，故B＝60°，由余弦定理，得 b2＝c2＋a2－2accos 60°，即b2＝c2＋a2－ac，‎ 故c2＋a2＝ac＋b2成立．于是原等式成立．‎ 归纳分析法证题的技巧 ‎1．逆向思考是用分析法证题的主要思想，通过反推，逐步寻找使结论成立的充分条件，正确把握转化方向是使问题顺利获解的关键．‎ ‎2．证明较复杂的问题时，可以采用两头凑的办法，即通过分析法找出某个与结论等价(或充分)的中间结论，然后通过综合法由条件证明这个中间结论，从而使原命题得证．‎ 在解题中注意引导学生自主分析和解决问题，教师及时点拨从而提高学生的解题能力和兴趣。‎ 教师引导学生及时总结，以帮助学生形成完整的认知结构。‎ 引导学生对所学的知识进行小结，由利于学生对已有的知识结构进行编码处理，加强理解记忆，提高解题技能。‎ 考点三 反证法 ‎(1)一个命题的结论是“自然数a，b，c中恰有一个偶数”，用反证法证明该命题时，正确的假设是(　　)‎ A．假设a，b，c都是奇数或至少有两个偶数 B．假设a，b，c都是偶数 C．假设a，b，c至少有两个偶数 D．假设a，b，c都是奇数 ‎(2)等差数列{an}的前n项和为Sn，a1＝1＋，S3＝9＋3.‎ ‎①求数列{an}的通项an与前n项和Sn；‎ ‎②设bn＝(n∈N*)，求证数列{bn}中任意不同的三项都不可能成为等比数列．‎ ‎【解析】　(1)“恰有一个”的否定是“一个也没有”或“至少有2个”，因此正确的假设是“假设a，b，c都是奇数或至少有两个偶数”，故选A.【答案】　A ‎(2)①由已知得∴d＝2，‎ 故an＝2n－1＋，Sn＝n(n＋)．‎ ‎②证明由(1)得bn＝＝n＋.‎ 假设数列{bn}中存在三项bp，bq，br(p，q，r∈N*，且互不相等)成等比数列，则b＝bpbr，‎ 即(q＋)2＝(p＋)(r＋)，∴(q2－pr)＋(2q－p－r)＝0，∵p，q，r∈N*，∴ ‎∴2＝pr，即(p－r)2＝0.∴p＝r，与p≠r矛盾．‎ ‎∴假设不成立，即数列{bn}中任意不同的三项都不可能成等比数列．‎ 跟踪训练 1.设{an}是公比为q的等比数列．‎ ‎(1)推导{an}的前n项和公式；‎ ‎(2)设q≠1，证明数列{an＋1}不是等比数列．‎ ‎【解】　(1)设{an}的前n项和为Sn，‎ 当q＝1时，Sn＝a1＋a1＋…＋a1＝na1；‎ 当q≠1时，Sn＝a1＋a1q＋a1q2＋…＋a1qn－1，①‎ qSn＝a1q＋a1q2＋…＋a1qn，②‎ ‎①－②得，(1－q)Sn＝a1－a1qn，‎ ‎∴Sn＝，∴Sn＝ ‎(2)证明假设{an＋1}是等比数列，则对任意的k∈N*，‎ ‎(ak＋1＋1)2＝(ak＋1)(ak＋2＋1)，‎ a＋2ak＋1＋1＝akak＋2＋ak＋ak＋2＋1，‎ aq2k＋2a1qk＝a1qk－1·a1qk＋1＋a1qk－1＋a1qk＋1，‎ ‎∵a1≠0，∴2qk＝qk－1＋qk＋1.∵q≠0，∴q2－2q＋1＝0，‎ ‎∴q＝1，这与已知矛盾．‎ ‎∴假设不成立，故{an＋1}不是等比数列．‎ 归纳反证法的适用范围及证题的关键 ‎1．适用范围当一个命题的结论是以“至多”、“至少”、“唯一”或以否定形式出现时，宜用反证法来证．‎ ‎2．关键在正确的推理下得出矛盾，矛盾可以是与已知条件矛盾，与假设矛盾，与定义、公理、定理矛盾，与事实矛盾等，推导出的矛盾必须是明显的．‎ 环节三 课堂小结 ‎1.了解直接证明的两种基本方法——分析法和综合法；了解分析法和综合法的思考过程和特点．‎ ‎2.了解反证法的思考过程和特点.‎ 学生回顾，总结.‎ 引导学生对学习过程进行反思，为在今后的学习中，进行有效调控打下良好的基础。‎ 环节四 课后作业学生版练与测 学生通过作业进行课外反思，通过思考发散巩固所学的知识。‎ ‎ ‎