浙江省杭州市建人高复2020届高三下学期4月模拟测试数学试题 Word版含解析 26页

www.ks5u.com 杭州建人高复2020届第二学期模拟测试数学试卷 本试卷分选择题和非选择题两部分.满分150分，考试时间120分钟.‎ 参考公式：‎ 如果事件互斥，那么柱体的体积公式 ‎；‎ 如果事件相互独立，那么椎体的体积公式 ‎；‎ 如果事件在一次试验中发生的概率是，那么球的表面积公式 次独立重复试验中事件A恰好发生次的概率 ‎（k=0，1，…，n）.球的体积公式 台体的体积公式 选择题部分（共40分）‎ 一、选择题：本大题共10小题，每小题4分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.已知全集2，3，4，5，，集合，，则　　‎ A. B. 3，5，‎ C. 3，4， D. 2，3，4，5，‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 进行并集、补集的运算即可．‎ ‎【详解】P∪Q={1，3，4，5}；∴∁U（P∪Q）={2，6}．‎ 故选A．‎ ‎【点睛】考查列举法表示集合概念，并集、补集的运算,属于基础题.‎ ‎2.已知a，b∈R，则“”是“”的（ ）‎ A. 充分不必要条件 B. 必要不充分条件 - 26 -‎ C. 充要条件 D. 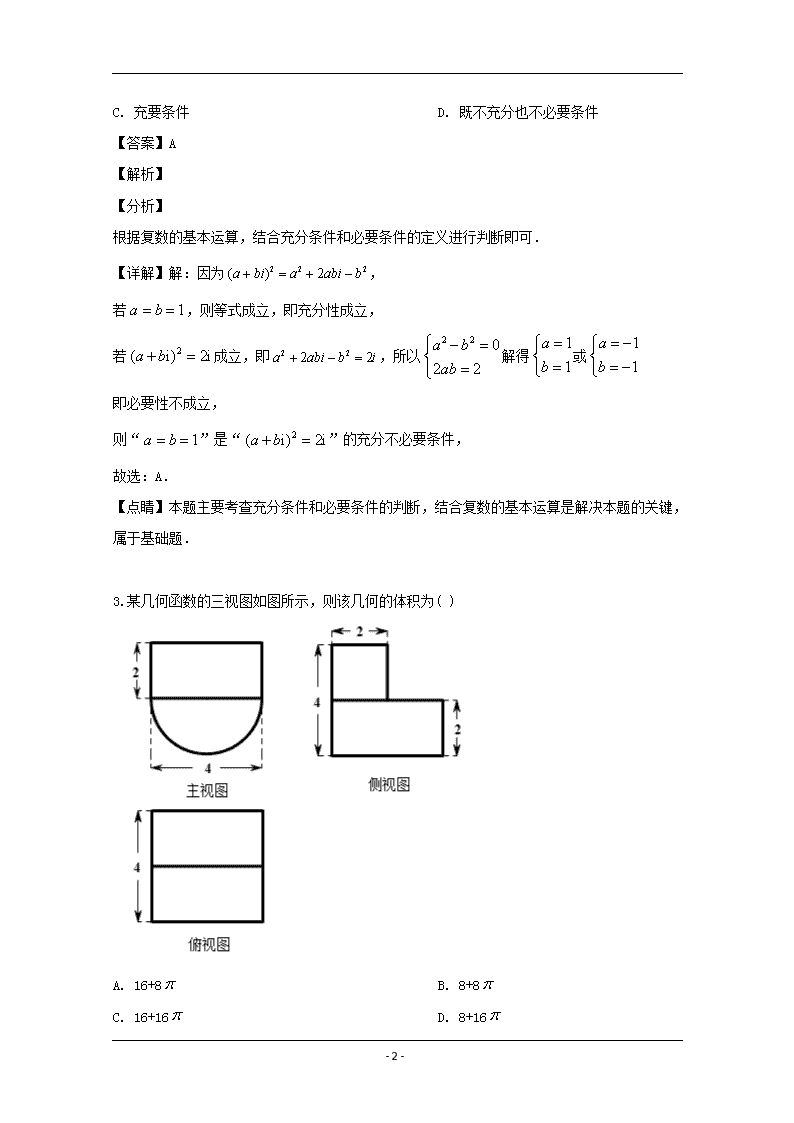既不充分也不必要条件 ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据复数的基本运算，结合充分条件和必要条件的定义进行判断即可．‎ ‎【详解】解：因为，‎ 若，则等式成立，即充分性成立，‎ 若成立，即，所以解得或 即必要性不成立，‎ 则“”是“”的充分不必要条件，‎ 故选：A．‎ ‎【点睛】本题主要考查充分条件和必要条件的判断，结合复数的基本运算是解决本题的关键，属于基础题．‎ ‎3.某几何函数的三视图如图所示，则该几何的体积为( )‎ A. 16+8 B. 8+8‎ C. 16+16 D. 8+16‎ - 26 -‎ ‎【答案】A ‎【解析】‎ 试题分析：由已知中的三视图可得该几何体是一个半圆柱和正方体的组合体，‎ 半圆柱的底面半径为2，故半圆柱的底面积半圆柱的高．‎ 故半圆柱的体积为，长方体的长宽高分别为故长方体的体积为 故该几何体的体积为，选A 考点：三视图，几何体的体积 ‎4.如果正数满足，那么（　　）‎ A. ，且等号成立时的取值唯一 B. ，且等号成立时的取值唯一 C. ，且等号成立时的取值不唯一 D. ，且等号成立时的取值不唯一 ‎【答案】A ‎【解析】‎ 正数满足，∴ 4=，即，当且仅当a=b=2时，“=”成立；又4=，∴ c+d≥4，当且仅当c=d=2时，“=”成立；综上得，且等号成立时的取值都为2，选A．‎ ‎5.设等差数列的公差为d，若数列为递减数列，则（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ 试题分析：因为是等差数列，则，又由于为递减数列，所以，故选C.‎ 考点：1.等差数列的概念；2.递减数列.‎ ‎6.已知实数满足则的最小值是（ ）‎ - 26 -‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据已知条件把转化为圆的标准方程，可得到圆心坐标及半径，而可转化为即可看到圆上的点到直线距离的最小值.‎ ‎【详解】，‎ ‎，即圆心，半径，‎ ‎，‎ 可看到圆上的点到直线距离，‎ 圆上的点到直线距离的最小值为 圆心到直线距离减去半径即，‎ ‎，‎ 圆上的点到直线距离的最小值为，‎ 的最小值为 - 26 -‎ 故选：A ‎【点睛】本题考查了圆上的点到定直线的距离的最小值，考查了学生的计算能力，属于一般题.‎ ‎7.定义平面向量之间的一种运算“”如下：对任意的，，令.下面说法错误的是 A. 若共线，则 B. ‎ C. 对任意的 D. ‎ ‎【答案】B ‎【解析】‎ ‎【详解】若与共线，则有，故A正确；因为，而，所以有，故选项B错误；‎ 因为，，所以选项C正确；‎ ‎，所以选项D正确.‎ 故选B．‎ ‎8.对于给定正数k，定义，设，对任意和任意恒有，则（ ）‎ A. k的最大值为2 B. k的最小值为2 C. k的最大值为1 D. k的最小值为1‎ ‎【答案】B ‎【解析】‎ - 26 -‎ ‎【分析】‎ 根据已知条件可得：对任意恒成立，即，结合二次函数的性质可求函数的最大值即可.‎ ‎【详解】因为对任意和任意恒有，‎ 根据已知条件可得：对任意恒成立，‎ 即，‎ ‎，‎ ‎，‎ 当时有，即 故选：B ‎【点睛】本题考查了不等式恒成立问题以及二次函数的性质，属于一般题.‎ ‎9.如图，点在正方体的表面上运动，且到直线与直线 的距离相等，如果将正方体在平面内展开，那么动点的轨迹在展开图中的形状是（ ）‎ A. B. ‎ - 26 -‎ C. D. ‎ ‎【答案】B ‎【解析】‎ 在平面BCC1B1上，‎ P到直线C1D1的距离为|PC1|，‎ ‎∵P到直线BC与直线C1D1的距离相等，‎ ‎∴点P到点C1的距离与到直线BC的距离相等，‎ ‎∴轨迹为抛物线,且点C1为焦点，BC为准线；‎ 故排除C，D，‎ 同理可得，‎ 在平面ABB1A1上，‎ 点P到点B的距离与到直线C1D1的距离相等，‎ - 26 -‎ 从而排除A，‎ 本题选择B选项.‎ ‎10.设函数的最大值为，最小值为，则（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 将函数整理为，再由辅助角公式和正弦函数的值域，得到不等式，结合韦达定理，即可得到答案.‎ ‎【详解】因为，‎ 所以有，即 ‎，为辅助角，‎ 因为，‎ 所以，‎ 化简得：，‎ 由于恒成立，‎ 则判别式：‎ 恒成立，‎ 即有不等式的解集为，‎ 由韦达定理可得 故选：D ‎【点睛】本题考查了利用三角函数的范围，辅助角公式以及韦达定理，考查了学生的计算能力，属于较难题.‎ - 26 -‎ 非选择题部分（共110分）‎ 二、填空题：本大题共7个小题，多空题每题6分，单空题每题4分，共36分.‎ ‎11.已知，若，则_______，______；‎ ‎【答案】 (1). (2). ‎ ‎【解析】‎ ‎【分析】‎ 根据已知条件可得，所以直接把代入即可求出，，即有，再代入计算即可.‎ ‎【详解】，‎ ‎，‎ ‎，‎ ‎，‎ ‎，‎ 故答案为：；‎ ‎【点睛】本题考查了对数，指数的运算，考查了学生的计算能力，属于一般题.‎ ‎12.已知方程，若该方程表示椭圆方程，则的取值范围是_______；‎ ‎【答案】或 ‎【解析】‎ ‎【分析】‎ 先对方程进行化简成椭圆的标准方程，再利用椭圆的定义可得到的取值范围.‎ ‎【详解】因为方程，‎ - 26 -‎ 所以，‎ 所以有即或 故答案为：或 ‎【点睛】本题考查了椭圆的定义，考查了学生的计算能力，属于较易题.‎ ‎13.已知展开式中各项的系数和比各项的二项式系数和大992，则展开式中最大的二项式系数为______；展开式中系数最大的项为______.‎ ‎【答案】 (1). 10 (2). ‎ ‎【解析】‎ ‎【分析】‎ 由题意令可得展开式中各项系数和为，二项式系数和，再根据已知条件可得到，即可求出.‎ ‎【详解】，‎ 令可得展开式中各项系数和为，且二项式系数和，‎ 展开式中各项的系数和比各项的二项式系数和大992，‎ 解得，‎ 则展开式中最大的二项式系数为；‎ 设展开式中第项的系数最大，‎ 由二项式定理可得展开式，‎ 则，‎ - 26 -‎ 所以，‎ 解得：，‎ 因为，‎ 所以，‎ 因此当时展开式中第5项系数最大的项为 故答案为：10；‎ ‎【点睛】本题考查了二项式的展开式以及系数和，考查了学生的计算能力，属于一般题.‎ ‎14.将字母放入的方表格，每个格子各放一个字母，则每一行的字母互不相同，每一列的字母也互不相同的概率为_______；若共有行字母相同，则得k分，则所得分数的数学期望为______；（注：横的为行，竖的为列；比如以下填法第二行的两个字母相同，第1，3行字母不同，该情况下）‎ a b c c a b ‎【答案】 (1). (2). （填0.6也对）‎ ‎【解析】‎ ‎【分析】‎ 分类讨论计算出满足条件的基本事件个数，以及所有的基本事件个数，代入概率计算公式即可；计算出对对应的得分数的概率，代入期望公式即可.‎ ‎【详解】第一种：当每一列都不一样时有：‎ 第一列三个全排有，第二列剩下的三个全排也有，‎ - 26 -‎ 第二种：在一列中有其中两个是一样的则有：，‎ 所以总的基本事件个数有：，‎ 当每一行的字母互不相同，每一列的字母也互不相同的基本事件个数有：‎ ‎，‎ 记事件“每一行的字母互不相同，每一列的字母也互不相同”为，‎ 则；‎ 因为所得分数可能取值为：0，1，3，‎ 则有：，‎ 所以有 故答案为：；‎ ‎【点睛】本题考查了离散型随机变量的概率和期望的计算，考查了学生的计算能力，属于一般题.‎ ‎15.已知正四面体和平面，，正四面体绕边旋转，当与平面所成角最大时，与平面所成角的正弦值为______‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 由已知条件可得当与平面所成角最大时即平面，以的中点为原点建立空间直角坐标系，写出相关点的坐标，代入线面角公式即可求出.‎ ‎【详解】由题意可得：当与平面所成角最大时即平面，‎ 以的中点为原点建立空间直角坐标系（如图），‎ - 26 -‎ 过作平面，垂足为，设，‎ 则，即,‎ 设与平面所成角为，平面的法向量为，‎ 则 即与平面所成角的正弦值为 故答案为：‎ ‎【点睛】本题考查了利用向量法求线面角的正弦值，考查了学生的计算能力，属于一般题.‎ ‎16.双曲线的左焦点为，过的直线交双曲线左支于两点，且，延长交双曲线右支于点，若，则该双曲线的离心率为_________‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 取双曲线的右焦点,连接，延长交双曲线于，连接，由平面几何的性质可得四边形为矩形，设，运用双曲线的定义和对称性，结合勾股定理，化简可得，代入方程结合离心率公式即可求出.‎ - 26 -‎ ‎【详解】取双曲线的右焦点,连接，延长交双曲线于，连接，（如图）‎ 由，‎ 可得四边形为矩形，‎ 设，‎ 由对称性可得：，，‎ 即有，‎ 由双曲线的定义可得：‎ ‎，①‎ 在直角三角形中，‎ ‎，‎ 可得，②‎ 由①②可得，即，‎ 代入①可得：，‎ 化简可得：，‎ 即有 故答案为：‎ ‎【点睛】本题考查了双曲线的定义以及性质，考查了学生的计算能力，属于较难题.‎ - 26 -‎ ‎17.已知都是单位向量，且，则的最小值为_____；最大值为________‎ ‎【答案】 (1). (2). ‎ ‎【解析】‎ ‎【分析】‎ 根据题意可设，再代入，利用二倍角公式进行化简、求三角函数的值域即可.‎ ‎【详解】因为都是单位向量，且，‎ 设，‎ 则 取当取时，‎ 即，‎ 则有 ‎，，‎ 此时有：，‎ 同理当时，有 - 26 -‎ ‎，，‎ 此时有：‎ 故的最小值为；最大值为 故答案为：；‎ ‎【点睛】本题考查了向量的坐标运算以及三角函数的化简、求值域，考查了学生的计算能力，属于较难题.‎ 三、简答题：本大题共5小题，共74分.解答应写出文字说明、证明过程和演算步骤.‎ ‎18.在中，角A，B，C所对的边分别为a，b，c，已知.‎ ‎（1）求角B的大小；‎ ‎（2）求的取值范围.‎ ‎【答案】（1） （2）‎ ‎【解析】‎ ‎【分析】‎ ‎(1)根据题意可利用正弦定理把边转化为角，再用两角和的正弦即可；‎ ‎(2)先利用二倍角公式进行化简，再利用角度范围即可求的取值范围.‎ ‎【详解】（1）由题意 - 26 -‎ ‎（2）‎ ‎【点睛】本题考查了正弦定理，两角和的正弦公式，二倍角公式，考查了学生的计算能力，属于一般题.‎ ‎19.如图所示，和所在平面互相垂直，且，，，分别为，的中点.‎ ‎（1）求证：；‎ ‎（2）求二面角的正弦值.‎ - 26 -‎ ‎【答案】(1)见解析(2) ‎ ‎【解析】‎ 试题分析：（1）（方法一）过E作EO⊥BC，垂足为O，连OF，由△ABC≌△DBC可证出△EOC≌△FOC，所以∠EOC=∠FOC=，即FO⊥BC，又EO⊥BC，因此BC⊥面EFO，即可证明EF⊥BC.（方法二）由题意，以B为坐标原点，在平面DBC内过B左垂直BC的直线为x轴，BC所在直线为y轴，在平面ABC内过B作垂直BC的直线为z轴，建立如图所示的空间直角坐标系.‎ 易得,所以，因此,从而得；（2） （方法一）在图1中，过O作OG⊥BF，垂足为G，连EG，由平面ABC⊥平面BDC，从而EO⊥平面BDC，从而EO⊥面BDC，又OG⊥BF，由三垂线定理知EG垂直BF，因此∠EGO为二面角E-BF-C平面角；在△EOC中，EO=EC=BC·cos30°=，由△BGO∽△BFC知，,因此tan∠EGO=,从而sin∠EGO=，即可求出二面角E-BF-C的正弦值.‎ ‎（方法二）在图2中，平面BFC的一个法向量为，设平面BEF的法向量，又,由得其中一个，设二面角E-BF-C的大小为，且由题意知为锐角，则，因此sin∠EGO=，即可求出二面角E-BF-C的正弦值.‎ - 26 -‎ ‎（1）证明：‎ ‎（方法一）过E作EO⊥BC，垂足为O，连OF，‎ 由△ABC≌△DBC可证出△EOC≌△FOC，所以∠EOC=∠FOC=，即FO⊥BC，‎ 又EO⊥BC，因此BC⊥面EFO，‎ 又EF面EFO，所以EF⊥BC.‎ ‎（方法二）由题意，以B为坐标原点，在平面DBC内过B左垂直BC的直线为x轴，BC所在直线为y轴，在平面ABC内过B作垂直BC的直线为z轴，建立如图所示的空间直角坐标系.‎ 易得B（0,0,0），A(0，-1，),D(,-1,0)，C(0,2,0),因而,所以，因此,从而，所以.‎ ‎（2）（方法一）在图1中，过O作OG⊥BF，垂足为G，连EG，由平面ABC⊥平面BDC，从而EO⊥平面BDC，从而EO⊥面BDC，又OG⊥BF，由三垂线定理知EG垂直BF.‎ 因此∠EGO为二面角E-BF-C的平面角；‎ 在△EOC中，EO=EC=BC·cos30°=，由△BGO∽△BFC知，,因此tan∠EGO=,从而sin∠EGO=，即二面角E-BF-C的正弦值为.‎ - 26 -‎ ‎（方法二）在图2中，平面BFC的一个法向量为，设平面BEF的法向量，又,由得其中一个，设二面角E-BF-C的大小为，且由题意知为锐角，则，因此sin∠EGO=，即二面角E-BF-C的正弦值为.‎ 考点：1.线面垂直的判定；2.二面角.‎ ‎20.已知各项均为正数的数列{}的前n项和满足，且 ‎（1）求{}的通项公式；‎ ‎（2）设数列满足，并记为前n项和，求证：‎ ‎【答案】（1）（2）见解析 ‎【解析】‎ ‎【分析】‎ ‎(1)利用已知与的关系求{}的通项公式；‎ ‎(2)先根据(1)的结论求出，再求出的前n项和，利用放缩法证明不等式.‎ ‎【详解】解：（1）由，因此 由 得，又，得 从而{}是首项为2公差为3的等差数列，故{}的通项公式为 ‎（2）由可得，从而 - 26 -‎ ‎=‎ 于是 ‎【点睛】本题考查了已知与的关系求{}的通项公式以及利用放缩法证明不等式，属于较难题.‎ ‎21.已知是抛物线上位于轴两侧的不同两点 ‎（1）若在直线上，且使得以为顶点的四边形恰为正方形，求该正方形的面积.‎ ‎（2）求过、的切线与直线围成的三角形面积的最小值；‎ ‎【答案】（1）或；（2）‎ ‎【解析】‎ ‎【分析】‎ ‎(1)联解直线方程和抛物线方程，可求出的弦长，再结合已知条件以为顶点的四边形为正方形可得到正方形的边长，从而可求得面积；‎ ‎(2)分别求出切线方程，由切线方程求出交点坐标，代入三角形的面积公式，利用基本不等式求出面积的最小值.‎ ‎【详解】（1）设直线 联立直线与抛物线方程得：‎ 易得：‎ - 26 -‎ 直线与之间的距离为 令，可得 所以该正方形的边长为或 面积为或；‎ ‎（2）设，（由对称性不妨设）‎ 则处的切线方程为：，与直线交点记为M，则 则处的切线方程为：，与直线交点记为N，则 两条切线交点P 于是 当时取到等号 - 26 -‎ 所以该三角形面积的最小值为 ‎【点睛】本题考查了直线与抛物线位置关系求弦长，求过点的切线方程，利用基本不等式求最小值，考查了学生的计算能力，属于较难题.‎ ‎22.设函数，其图象与x轴交于A（x1，0），B（x2，0）两点，且x1＜x2．‎ ‎（1）求的取值范围；‎ ‎（2）证明：f′（）＜0（f′（x）为函数f（x）的导函数）；‎ ‎（3）设点C在函数y＝f（x）的图象上，且△ABC为等腰直角三角形，记t，求（﹣1）（t﹣1）的值．‎ ‎【答案】（1）见解析; （2）见解析（3）2‎ ‎【解析】‎ ‎【详解】（1）∵f（x）＝ex﹣ax+a，‎ ‎∴f'（x）＝ex﹣a，‎ 若a≤0，则f'（x）＞0，则函数f（x）是单调增函数，这与题设矛盾．‎ ‎∴a＞0，令f'（x）＝0，则x＝lna，‎ 当f'（x）＜0时，x＜lna，f（x）是单调减函数，‎ 当f'（x）＞0时，x＞lna，f（x）是单调增函数，‎ 于是当x＝lna时，f（x）取得极小值，‎ ‎∵函数f（x）＝ex﹣ax+a（a∈R）的图象与x轴交于两点A（x1，0），B（x2，0）（x1＜x2），‎ ‎∴f（lna）＝a（2﹣lna）＜0，即a＞e2，‎ 此时，存在1＜lna，f（1）＝e＞0，‎ 存在3lna＞lna，f（3lna）＝a3﹣3alna+a＞a3﹣3a2+a＞0，‎ 又由f（x）在（﹣∞，lna）及（lna，+∞）上的单调性及曲线在R上不间断，‎ 可知a＞e2为所求取值范围．‎ - 26 -‎ ‎（2）∵，‎ ‎∴两式相减得．‎ 记，则，‎ 设g（s）＝2s﹣（es﹣e﹣s），‎ 则g'（s）＝2﹣（es+e﹣s）＜0，‎ ‎∴g（s）是单调减函数，‎ 则有g（s）＜g（0）＝0，而，‎ ‎∴．‎ 又f'（x）＝ex﹣a是单调增函数，且 ‎∴． ‎ ‎（3）依题意有，则⇒xi＞1（i＝1，2）．‎ 于是，在等腰三角形ABC中，显然C＝90°，‎ ‎∴，即y0＝f（x0）＜0，‎ 由直角三角形斜边的中线性质，可知，‎ ‎∴，‎ 即，‎ ‎∴，‎ 即．‎ - 26 -‎ ‎∵x1﹣1≠0，则，‎ 又，‎ ‎∴，‎ 即，‎ ‎∴（a﹣1）（t﹣1）＝2．‎ 点睛：本题以含参数的函数解析式为背景，旨在考查导数的有关知识在研究函数的单调性与极值（最值）等方面的综合运用．求解第一问时，充分借助题设条件运用分析推证的思想方法求解；解答第二问时，则借助题设中的坐标进分析推证；第三问则依据等边三角形的题设条件进行分析探求，综合运用等价转化的数学思想及数形结合的思想和意识，从而使得问题简捷、巧妙地获解．‎ - 26 -‎ - 26 -‎