- 972.00 KB
- 2023-11-08 发布
台州市 2011学年 第一学期 高三年级期末质量评估试题
数 学(文) 2012.01
本试题卷分选择题和非选择题两部分.满分150分,考试时间120分钟.
Ⅰ 选择题部分(共50分)
参考公式:
球的表面积公式 柱体的体积公式
球的体积公式 其中表示柱体的底面积,h表示柱体的高
其中表示球的半径 台体的体积公式
锥体的体积公式 其中,分别表示台体的上底、下底面积,
其中表示锥体的底面积,表示锥体的高 表示台体的高
如果事件,互斥,那么
一、选择题(共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项符合题目要求.)
1. 复数等于
(A) (B) (C) (D)
2. 集合,集合,则
(A) (B) (C) (D)
3.向量,则“”是“∥”的
(A) 充分而不必要条件 (B) 必要而不充分条件
(C) 充要条件 (D) 既不充分也不必要条件
4. 已知点及圆 ,则过点,且在圆上截得最长的弦所在的直线方程是
(A) (B) (C) (D)
5. 设函数为偶函数,且当时,当时,则
(A) (B) (C) (D)
开始
S=S+k
结束
输出
是
否
6. 按照如图的程序框图执行,若输出结果为,则处条件为
(A)? (B)?
(C)? (D)?
7. 若函数在R上既是奇函
(第6题)
(A) (B) (C) (D)
数,又是减函数,则的图象是
8. 设斜率为的直线与椭圆交于不同的两点,且这两个交点在轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为
(A) (B) (C) (D)
9. 如图,正方体中,是棱的中点,是
侧面上的动点,且//平面,则与平面
所成角的正弦值构成的集合是
(第9题)
(A) (B)
(第10题)
(C) (D)
10. 定义在上R的函数满足,为的导函 数,已知的图象如图所示,若两个正数满足,则的取值范围是
(A) (B)
(C) (D)
Ⅱ 非选择题部分(共100分)
二、填空题(本题共7道小题,每题4分,共28分;将答案直接答在答题卷上指定的位置)
(第11题)
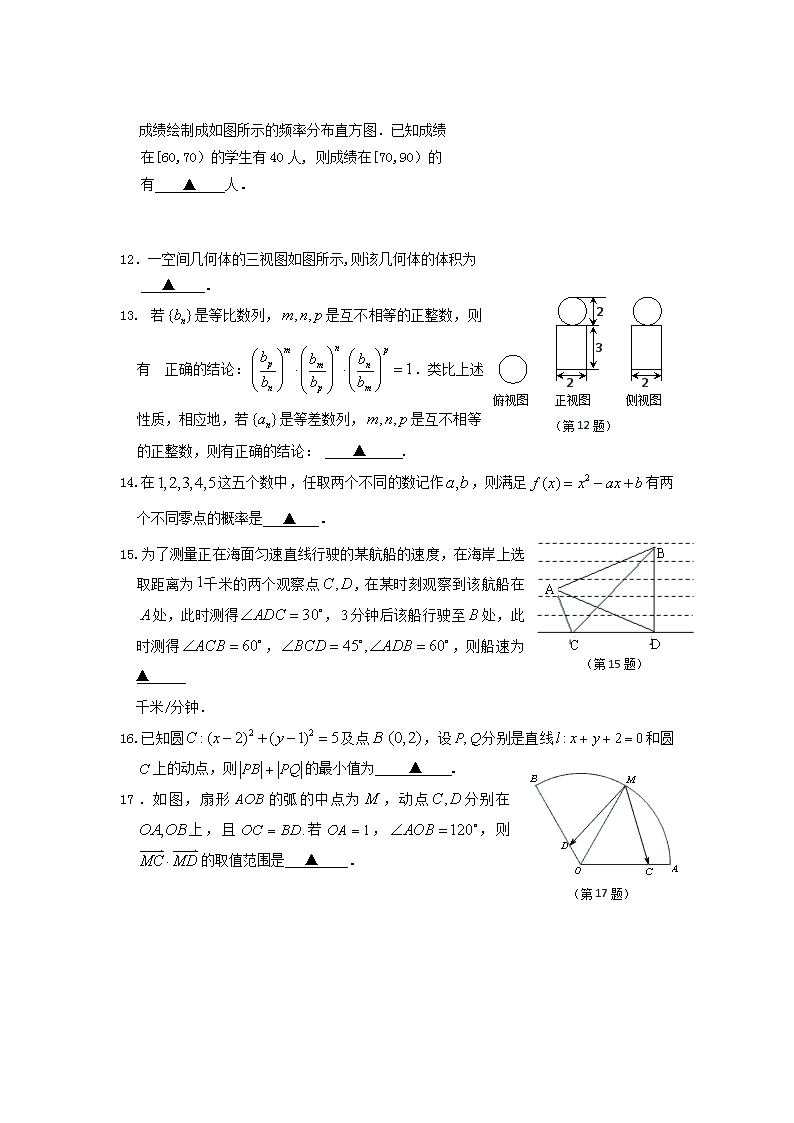
11.在某次法律知识竞赛中,将来自不同学校的学生的
成绩绘制成如图所示的频率分布直方图.已知成绩
在[60,70)的学生有40人, 则成绩在[70,90)的
有 ▲ 人.
12.一空间几何体的三视图如图所示,则该几何体的体积为
▲ .
俯视图
正视图
侧视图
2
3
2
2
(第12题)
13.若是等比数列,是互不相等的正整数,则有 正确的结论:.类比上述性质,相应地,若是等差数列,是互不相等的正整数,则有正确的结论: ▲ .
14.在这五个数中,任取两个不同的数记作,则满足有两个不同零点的概率是 ▲ .
B
C
A
(第15题)
D
15.为了测量正在海面匀速直线行驶的某航船的速度,在海岸上选取距离为千米的两个观察点,在某时刻观察到该航船在处,此时测得,分钟后该船行驶至处,此时测得,,则船速为 ▲
千米/分钟.
(第17题)
16.已知圆及点,设分别是直线和圆上的动点,则的最小值为 ▲ .
17.如图,扇形的弧的中点为,动点分别在上,且若,,则的取值范围是 ▲ .
三、解答题(本题共5小题,共72分.解答应写出文字说明、证明过程或演算步骤.)
18.(本题满分14分)已知函数的最小正周期为,最大值为3.
(Ⅰ)求和常数的值;
(Ⅱ)求函数的单调递增区间.
19. (本题满分14分)已知数列是首项为,公比为的等比数列.数列满足,是的前项和.
(Ⅰ)求
(第20题)
)
(Ⅱ)设同时满足条件:①;②(,是与无关的常数)的无穷数列叫“特界”数列.判断(1)中的数列是否为“特界”数列,并说明理由.
20.(本题满分14分)如图,在三棱锥中, ,,为线段的中点.
(Ⅰ)求证:;
(Ⅱ)求二面角的余弦值.
21. (本题满分15分)已知函数.
(Ⅰ)当时,求函数的极大值;
(Ⅱ)若函数存在单调递减区间,求实数的取值范围.
22.(本题满分15分)已知抛物线的焦点为,过点的直线与相交于两点,点关于轴的对称点为.
(Ⅰ)证明:点在直线上;
(Ⅱ)设,求的平分线与轴的交点坐标.
学校________________________ 班级_______________________ 姓名________________________ 准考证号_____________________________
…………………………………………装……………………………………订……………………………………线……………………………………
台州市 2011学年 第一学期 高三年级期末质量评估试题
数 学(文)答题卷2012.01
题号
一
二
18
19
20
21
22
总分
分数
一、选择题:本大题共有10小题,每小题5分,共50分.
题号
1
2
3
4
5
6
7
8
9
10
答案
二、填空题:本大题共有7小题,每小题4分,共28分.
11.________________________ 12.________________________
13. 14.________________________
15.________________________ 16.________________________
17.________________________
18.
三、解答题:本大题共5小题,共72分.解答应写出文字说明,证明过程或演算步骤.
请在各题目的答题区域内作答,超出边框限定区域的答案无效
19.
20.
请在各题目的答题区域内作答,超出边框限定区域的答案无效
21.
请在各题目的答题区域内作答,超出边框限定区域的答案无效
…………………………………………装……………………………………订……………………………………线……………………………………
22.
请在各题目的答题区域内作答,超出边框限定区域的答案无效
台州市2011学年第一学期高三年级期末质量评估试题
数学(文)参考答案及评分标准
2012.1
一、选择题:
1-10.
二、填空题:
11. 12. 13.
14. 15. 16. 17.
三、解答题:
18.(本小题14分)
(I)解: ……………………………………1分
, ………………………3分
由,得. ………………………5分
又当时,,得. ………7分
(Ⅱ)解:由(I)知,由,9分
得, ………………12分
故的单调增区间为. …………………14分
19.(本小题14分)
(I)解:, …………2分
, …………4分
. …………7分
(Ⅱ)解:由,
得,故数列适合条件①; …………………10分
又,故当或时,有最大值20,
即,故数列适合条件②. …………13分
综上,数列是“特界”数列. …………14分
O
A
B
C
D
M
N
20.(本小题14分)
(Ⅰ)证:取的中点,连接,则,
∵平面⊥平面,∴⊥平面,
∴⊥. ………3分
又∵平面,∴⊥. ………6分
∵∩=,∴⊥平面.…………………7分
(第20题)
(Ⅱ)解:取的中点,连接,
则∥,∴⊥平面,∴⊥. …………………8分
∵⊥,∥,∴⊥.
又∵∩=,∴⊥平面,
∴⊥,∴∠是所求二面角的平面角. ………11分
在Rt△中,,,
∴==,∴cos∠==. ………………14分
(其它解法相应给分)
21.(本题满分15分)
(Ⅰ)解:,. ……………2分
由,得,由,得. ……………5分
所以存在极大值. ……………7分
(Ⅱ)解:, ……………8分
依题意在上有解,即在上有解. …………9分
当时,显然有解; ……………11分
当时,由方程至少有一个正根,得; ……………14分
所以. ……………15分
另解:依题意在上有解,即在上有解. ………9分
在上有解,即 , ………11分
由,得. ……………15分
22.(本题满分15分)
(Ⅰ)解:设,,的方程为,
由得,
从而,. …………2分
直线的方程为,即,
令,得,所以点在直线上. …………6分(Ⅱ)解:因为 ,
故,解得, …………9分
所以的方程为.
又由(Ⅰ)得 ,故直线的斜率为,
因而直线的方程为. ……12分
设的平分线与轴的交点为,
则到及的距离分别为 ,,
由,得,或(舍去),
所以的平分线与轴的交点为. ……15分