高考理数　直线、平面垂直的判定与性质 87页

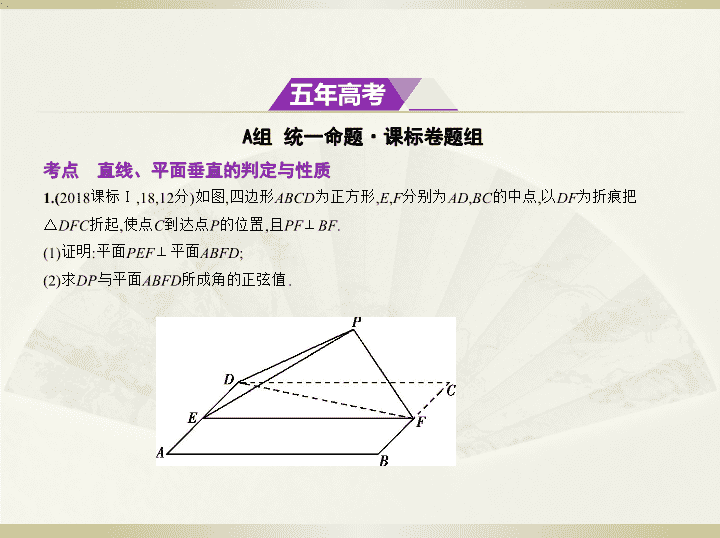
§8.3 　直线、平面垂直的判定与性质 高考理数 (课标专用 ) A组  统一命题·课标卷题组 考点　直线、平面垂直的判定与性质 1.( 2018课标Ⅰ,18,12分)如图,四边形 ABCD 为正方形, E , F 分别为 AD , BC 的中点,以 DF 为折痕把 △ DFC 折起,使点 C 到达点 P 的位置,且 PF ⊥ BF . (1)证明:平面 PEF ⊥平面 ABFD ; (2)求 DP 与平面 ABFD 所成角的正弦值.   五年高考 解析 　(1)由已知可得 BF ⊥ EF , 又已知 BF ⊥ PF ,且 PF 、 EF ⊂ 平面 PEF , PF ∩ EF = F , 所以 BF ⊥平面 PEF , 又 BF ⊂ 平面 ABFD ,所以平面 PEF ⊥平面 ABFD . (2)作 PH ⊥ EF ,垂足为 H .由(1)得, PH ⊥平面 ABFD . 以 H 为坐标原点,   的方向为 y 轴正方向,|   |为单位长,建立如图所示的空间直角坐标系 H - xyz .   由(1)可得, DE ⊥ PE .又 DP =2, DE =1,所以 PE =   , 又 PF =1, EF =2,故 PE ⊥ PF , 可得 PH =   , EH =   , 则 H (0,0,0), P   , D   ,   =   ,   =   为平面 ABFD 的法向量. 设 DP 与平面 ABFD 所成角为 θ ,则sin θ =   =   =   . 所以 DP 与平面 ABFD 所成角的正弦值为   . 易错警示 　利用空间向量求线面角的注意事项 (1)先求出直线的方向向量与平面的法向量所夹的锐角(钝角时取其补角)的角度,再取其余角 即为所求. (2)若求线面角的余弦值,要注意利用平方关系sin 2 θ +cos 2 θ =1求出其值,不要误以为直线的方向 向量与平面的法向量所夹角的余弦值为所求. 2. (2017课标Ⅲ,19,12分)如图,四面体 ABCD 中,△ ABC 是正三角形,△ ACD 是直角三角形,∠ ABD =∠ CBD , AB = BD . (1)证明:平面 ACD ⊥平面 ABC ; (2)过 AC 的平面交 BD 于点 E ,若平面 AEC 把四面体 ABCD 分成体积相等的两部分,求二面角 D - AE - C 的余弦值. 解析 　本题考查面面垂直的证明,二面角的求法. (1)由题设可得,△ ABD ≌△ CBD ,从而 AD = DC . 又△ ACD 是直角三角形,所以∠ ADC =90 ° . 取 AC 的中点 O ,连接 DO , BO ,则 DO ⊥ AC , DO = AO . 又由于△ ABC 是正三角形,故 BO ⊥ AC . 所以∠ DOB 为二面角 D - AC - B 的平面角. 在Rt△ AOB 中, BO 2 + AO 2 = AB 2 . 又 AB = BD ,所以 BO 2 + DO 2 = BO 2 + AO 2 = AB 2 = BD 2 ,故∠ DOB =90 ° . 所以平面 ACD ⊥平面 ABC . (2)由题设及(1)知, OA , OB , OD 两两垂直.以 O 为坐标原点,   的方向为 x 轴正方向,|   |为单位长, 建立如图所示的空间直角坐标系 O - xyz .则 A (1,0,0), B (0,   ,0), C (-1,0,0), D (0,0,1).   由题设知,四面体 ABCE 的体积为四面体 ABCD 的体积的   ,从而 E 到平面 ABC 的距离为 D 到平面 ABC 的距离的   ,即 E 为 DB 的中点,得 E   .故   =(-1,0,1),   =(-2,0,0),   =   . 设 n =( x , y , z )是平面 DAE 的法向量, 则   即   可取 n =   . 设 m 是平面 AEC 的法向量,则   同理可取 m =(0,-1,   ). 则cos< n , m >=   =   . 易知二面角 D - AE - C 为锐二面角, 所以二面角 D - AE - C 的余弦值为   . 方法总结 　证明面面垂直最常用的方法是证明其中一个平面经过另一个平面的一条垂线,即 在一个平面内,找一条直线,使它垂直于另一个平面.用空间向量法求二面角的余弦值时,要判 断二面角是钝角还是锐角. 3. (2016课标Ⅰ,18,12分)如图,在以 A , B , C , D , E , F 为顶点的五面体中,面 ABEF 为正方形, AF =2 FD ,∠ AFD =90 ° ,且二面角 D - AF - E 与二面角 C - BE - F 都是60 ° . (1)证明:平面 ABEF ⊥平面 EFDC ; (2)求二面角 E - BC - A 的余弦值. 解析 　(1)由已知可得 AF ⊥ DF , AF ⊥ FE ,所以 AF ⊥平面 EFDC .   (2分) 又 AF ⊂ 平面 ABEF ,故平面 ABEF ⊥平面 EFDC .   (3分) (2)过 D 作 DG ⊥ EF ,垂足为 G ,由(1)知 DG ⊥平面 ABEF . 以 G 为坐标原点,   的方向为 x 轴正方向,|   |为单位长,建立如图所示的空间直角坐标系 G - xyz .   (6分) 由(1)知∠ DFE 为二面角 D - AF - E 的平面角,故∠ DFE =60 ° ,则| DF |=2,| DG |=   ,可得 A (1,4,0), B (-3, 4,0), E (-3,0,0), D (0,0,   ). 由已知得, AB ∥ EF ,所以 AB ∥平面 EFDC .   (8分) 又平面 ABCD ∩ 平面 EFDC = CD , 故 AB ∥ CD , CD ∥ EF . 由 BE ∥ AF , 可得 BE ⊥ 平面 EFDC , 所以∠ CEF 为二面角 C - BE - F 的平面角 ,∠ CEF =60 ° . 从而可得 C (-2,0,   ). 所以   =(1,0,   ),   =(0,4,0),   =(-3,-4,   ),   =(-4,0,0).   (10 分 ) 设 n =( x , y , z ) 是平面 BCE 的法向量 , 则   即   所以可取 n =(3,0,-   ). 设 m 是平面 ABCD 的法向量,则   同理可取 m =(0,   ,4).则cos < n , m >=   =-   . 又易知二面角 E - BC - A 为钝二面角, 故二面角 E - BC - A 的余弦值为-   .   (12分) 思路分析 　(1)根据已知条件证出 AF ⊥平面 EFDC ,进而得出平面 ABEF ⊥平面 EFDC ;(2)根据证 得的垂直关系建立空间直角坐标系,求出平面 BCE 、平面 ABCD 的法向量,进而可求得二面角 E - BC - A 的余弦值. 方法总结 　对于立体几何问题的求解,首先要熟练掌握平行与垂直的判定与性质,对于面面垂 直的证明,寻找平面的垂线往往是解题的关键. 4 .(2015课标Ⅰ,18,12分)如图,四边形 ABCD 为菱形,∠ ABC =120 ° , E , F 是平面 ABCD 同一侧的两 点, BE ⊥平面 ABCD , DF ⊥平面 ABCD , BE =2 DF , AE ⊥ EC . (1)证明:平面 AEC ⊥平面 AFC ; (2)求直线 AE 与直线 CF 所成角的余弦值.   解析 　(1)连接 BD .设 BD ∩ AC = G ,连接 EG , FG , EF . 在菱形 ABCD 中,不妨设 GB =1.由∠ ABC =120 ° ,可得 AG = GC =   . 由 BE ⊥平面 ABCD , AB = BC ,可知 AE = EC . 又 AE ⊥ EC ,所以 EG =   ,且 EG ⊥ AC . 在Rt△ EBG 中,可得 BE =   ,故 DF =   . 在Rt△ FDG 中,可得 FG =   . 在直角梯形 BDFE 中,由 BD =2, BE =   , DF =   ,可得 EF =   . 从而 EG 2 + FG 2 = EF 2 ,所以 EG ⊥ FG . 又 AC ∩ FG = G ,可得 EG ⊥平面 AFC . 因为 EG ⊂ 平面 AEC ,所以平面 AEC ⊥平面 AFC .   (6分) (2)如图,以 G 为坐标原点,分别以   ,   的方向为 x 轴, y 轴正方向,|   |为单位长,建立空间直角 坐标系 G - xyz .   由(1)可得 A (0,-   ,0), E (1,0,   ), F   , C (0,   ,0),所以   =(1,   ,   ),   =   .   (10分) 故cos<   ,   >=   =-   . 所以直线 AE 与直线 CF 所成角的余弦值为   .   (12分) 5 .(2014课标Ⅰ,19,12分,0.428)如图,三棱柱 ABC - A 1 B 1 C 1 中,侧面 BB 1 C 1 C 为菱形, AB ⊥ B 1 C . (1)证明: AC = AB 1 ; (2)若 AC ⊥ AB 1 ,∠ CBB 1 =60 ° , AB = BC ,求二面角 A - A 1 B 1 - C 1 的余弦值.   解析 　(1)连接 BC 1 ,交 B 1 C 于点 O ,连接 AO .因为侧面 BB 1 C 1 C 为菱形,所以 B 1 C ⊥ BC 1 ,且 O 为 B 1 C 及 BC 1 的中点. 又 AB ⊥ B 1 C ,所以 B 1 C ⊥平面 ABO .由于 AO ⊂ 平面 ABO ,故 B 1 C ⊥ AO .又 B 1 O = CO ,故 AC = AB 1 . (2)因为 AC ⊥ AB 1 ,且 O 为 B 1 C 的中点,所以 AO = CO . 又因为 AB = BC ,所以△ BOA ≌△ BOC .故 OA ⊥ OB ,从而 OA , OB , OB 1 两两垂直. 以 O 为坐标原点,   的方向为 x 轴正方向,|   |为单位长,建立如图所示的空间直角坐标系 O - xyz .   因为∠ CBB 1 =60 ° ,所以△ CBB 1 为等边三角形,又 AB = BC ,则 A   , B (1,0,0), B 1   , C   .   =   ,   =   =   ,   =   =   . 设 n =( x , y , z )是平面 AA 1 B 1 的法向量, 则   即   所以可取 n =(1,   ,   ). 设 m 是平面 A 1 B 1 C 1 的法向量,则   同理可取 m =(1,-   ,   ). 则cos< n , m >=   =   . 易知二面角 A - A 1 B 1 - C 1 为锐二面角,所以二面角 A - A 1 B 1 - C 1 的余弦值为   . 方法点拨 　在求解或证明过程中,通常会用到一些初中阶段学习的平面几何知识,如三角形中 位线的性质、菱形的性质,等腰三角形的性质,相似(全等)三角形的判定与性质等,在复习时应 予以关注. 考点　直线、平面垂直的判定与性质 1 .(2014广东,7,5分)若空间中四条两两不同的直线 l 1 , l 2 , l 3 , l 4 ,满足 l 1 ⊥ l 2 , l 2 ⊥ l 3 , l 3 ⊥ l 4 ,则下列结论一 定正确的是   (　　) A. l 1 ⊥ l 4 　     B. l 1 ∥ l 4 C. l 1 与 l 4 既不垂直也不平行　     D. l 1 与 l 4 的位置关系不确定 B组  自主命题·省(区、市)卷题组 答案    D 　由 l 1 ⊥ l 2 , l 2 ⊥ l 3 可知 l 1 与 l 3 的位置不确定, 若 l 1 ∥ l 3 ,则结合 l 3 ⊥ l 4 ,得 l 1 ⊥ l 4 ,所以排除选项B、C, 若 l 1 ⊥ l 3 ,则结合 l 3 ⊥ l 4 ,知 l 1 与 l 4 可能不垂直,所以排除选项A.故选D. 评析 　本题考查了空间直线之间的位置关系,考查学生的空间想象能力、思维的严密性. 2 .(2018北京,16,14分)如图,在三棱柱 ABC - A 1 B 1 C 1 中, CC 1 ⊥平面 ABC , D , E , F , G 分别为 AA 1 , AC , A 1 C 1 , BB 1 的中点, AB = BC =   , AC = AA 1 =2. (1)求证: AC ⊥平面 BEF ; (2)求二面角 B - CD - C 1 的余弦值; (3)证明:直线 FG 与平面 BCD 相交.   解析 　(1)在三棱柱 ABC - A 1 B 1 C 1 中, 因为 CC 1 ⊥平面 ABC ,所以四边形 A 1 ACC 1 为矩形. 又 E , F 分别为 AC , A 1 C 1 的中点,所以 AC ⊥ EF . 因为 AB = BC ,所以 AC ⊥ BE . 所以 AC ⊥平面 BEF . (2)由(1)知 AC ⊥ EF , AC ⊥ BE , EF ∥ CC 1 . 又 CC 1 ⊥平面 ABC ,所以 EF ⊥平面 ABC .因为 BE ⊂ 平面 ABC ,所以 EF ⊥ BE . 如图建立空间直角坐标系 E - xyz .   由题意得 B (0,2,0), C (-1,0,0), D (1,0,1), F (0,0,2), G (0,2,1). 所以   =(-1,-2,0),   =(1,-2,1). 设平面 BCD 的法向量为 n =( x 0 , y 0 , z 0 ), 则   即   令 y 0 =-1,则 x 0 =2, z 0 =-4. 于是 n =(2,-1,-4). 又因为平面 CC 1 D 的一个法向量为   =(0,2,0), 所以cos< n ,   >=   =-   . 由题知二面角 B - CD - C 1 为钝角,所以其余弦值为-   . (3)由(2)知平面 BCD 的一个法向量为 n =(2,-1,-4),   =(0,2,-1). 因为 n ·   =2 × 0+(-1) × 2+(-4) × (-1)=2 ≠ 0, 所以直线 FG 与平面 BCD 相交. 3. (2015北京,17,14分)如图,在四棱锥 A - EFCB 中,△ AEF 为等边三角形,平面 AEF ⊥平面 EFCB , EF ∥ BC , BC =4, EF =2 a ,∠ EBC =∠ FCB =60 ° , O 为 EF 的中点. (1)求证: AO ⊥ BE ; (2)求二面角 F - AE - B 的余弦值; (3)若 BE ⊥平面 AOC ,求 a 的值.   解析 　(1)证明:因为△ AEF 是等边三角形, O 为 EF 的中点,所以 AO ⊥ EF . 又因为平面 AEF ⊥平面 EFCB , AO ⊂ 平面 AEF , 所以 AO ⊥平面 EFCB . 所以 AO ⊥ BE . (2)取 BC 中点 G ,连接 OG . 由题设知 EFCB 是等腰梯形, 所以 OG ⊥ EF . 由(1)知 AO ⊥平面 EFCB , 又 OG ⊂ 平面 EFCB , 所以 OA ⊥ OG . 如图建立空间直角坐标系 O - xyz , 则 E ( a ,0,0), A (0,0,   a ), B (2,   (2- a ),0),   =(- a ,0,   a ),   =( a -2,   ( a -2),0). 设平面 AEB 的法向量为 n =( x , y , z ), 则   即   令 z =1,则 x =   , y =-1. 于是 n =(   ,-1,1). 平面 AEF 的法向量为 p =(0,1,0). 所以cos< n , p >=   =-   . 由题设知二面角 F - AE - B 为钝二面角,所以它的余弦值为-   . (3)因为 BE ⊥平面 AOC ,所以 BE ⊥ OC ,即   ·   =0. 因为   =( a -2,   ( a -2),0),   =(-2,   (2- a ),0), 所以   ·   =-2( a -2)-3( a -2) 2 . 由   ·   =0及0< a <2,解得 a =   . 评析 　本题主要考查面面垂直的性质定理、二面角的求解以及线面垂直的性质定理,考查学 生空间想象能力和运算求解能力,正确建立空间直角坐标系以及表示点的坐标是解决本题的 关键. 4. (2015湖北,19,12分)《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马 P - ABCD 中,侧棱 PD ⊥底面 ABCD ,且 PD = CD ,过棱 PC 的中点 E ,作 EF ⊥ PB 交 PB 于点 F ,连接 DE , DF , BD , BE . (1)证明: PB ⊥平面 DEF .试判断四面体 DBEF 是不是鳖臑,若是,写出其每个面的直角(只需写出 结论);若不是,说明理由; (2)若面 DEF 与面 ABCD 所成二面角的大小为   ,求   的值. 解析　 解法一:(1)因为 PD ⊥底面 ABCD ,所以 PD ⊥ BC , 由底面 ABCD 为长方形,有 BC ⊥ CD ,而 PD ∩ CD = D , 所以 BC ⊥平面 PCD ,而 DE ⊂ 平面 PCD ,所以 BC ⊥ DE . 又因为 PD = CD ,点 E 是 PC 的中点,所以 DE ⊥ PC . 而 PC ∩ BC = C ,所以 DE ⊥平面 PBC . 而 PB ⊂ 平面 PBC ,所以 PB ⊥ DE . 又 PB ⊥ EF , DE ∩ EF = E ,所以 PB ⊥平面 DEF . 又因为 PD ⊥底面 ABCD ,所以 PD ⊥ DG . 而 PD ∩ PB = P ,所以 DG ⊥平面 PBD . 故∠ BDF 是面 DEF 与面 ABCD 所成二面角的平面角, 设 PD = DC =1, BC = λ ,有 BD =   , 在Rt△ PDB 中,由 DF ⊥ PB ,得∠ DPF =∠ FDB =   , 则tan   =tan∠ DPF =   =   =   ,解得 λ =   . 所以   =   =   . 故当面 DEF 与面 ABCD 所成二面角的大小为   时,   =   . 由 DE ⊥平面 PBC , PB ⊥平面 DEF ,可知四面体 BDEF 的四个面都是直角三角形,即四面体 BDEF 是一个鳖臑,其四个面的直角分别为∠ DEB ,∠ DEF ,∠ EFB ,∠ DFB . (2)如图,在面 PBC 内,延长 BC 与 FE 交于点 G ,则 DG 是平面 DEF 与平面 ABCD 的交线. 由(1)知, PB ⊥平面 DEF ,所以 PB ⊥ DG . 解法二:(1)如图,以 D 为原点,射线 DA , DC , DP 分别为 x , y , z 轴的正半轴,建立空间直角坐标系. 设 PD = DC =1, BC = λ ,则 D (0,0,0), P (0,0,1), B ( λ ,1,0), C (0,1,0),   =( λ ,1,-1),点 E 是 PC 的中点, 所以 E   ,   =   , 于是   ·   =0,即 PB ⊥ DE . 又已知 EF ⊥ PB ,而 DE ∩ EF = E ,所以 PB ⊥平面 DEF . 因   =(0,1,-1),   ·   =0,则 DE ⊥ PC ,所以 DE ⊥平面 PBC . 由 DE ⊥平面 PBC , PB ⊥平面 DEF ,可知四面体 BDEF 的四个面都是直角三角形, 即四面体 BDEF 是一个鳖臑,其四个面的直角分别为∠ DEB ,∠ DEF ,∠ EFB ,∠ DFB . (2)由 PD ⊥平面 ABCD ,所以   =(0,0,1)是平面 ABCD 的一个法向量; 由(1)知, PB ⊥平面 DEF ,所以   =(- λ ,-1,1)是平面 DEF 的一个法向量. 若面 DEF 与面 ABCD 所成二面角的大小为   , 则cos   =   =   =   , 解得 λ =   ,所以   =   =   . 故当面 DEF 与面 ABCD 所成二面角的大小为   时,   =   . 5 .(2014辽宁,19,12分)如图,△ ABC 和△ BCD 所在平面互相垂直,且 AB = BC = BD =2,∠ ABC =∠ DBC =120 ° , E , F 分别为 AC , DC 的中点. (1)求证: EF ⊥ BC ; (2)求二面角 E - BF - C 的正弦值.   解析 　(1)证法一:过 E 作 EO ⊥ BC ,垂足为 O ,连 OF ,如图1.   图1 由△ ABC ≌△ DBC 可证出△ EOC ≌△ FOC . 所以∠ EOC =∠ FOC =   , 即 FO ⊥ BC . 又 EO ⊥ BC ,因此 BC ⊥面 EFO . 又 EF ⊂ 面 EFO ,所以 EF ⊥ BC . 证法二:以 B 为坐标原点,在平面 DBC 内过 B 且垂直 BC 的直线为 x 轴, BC 所在直线为 y 轴,在平面 ABC 内过 B 且垂直 BC 的直线为 z 轴,建立如图2所示空间直角坐标系,   图2 易得 B (0,0,0), A (0,-1,   ), D (   ,-1,0), C (0,2,0),因而 E   , F   , 所以,   =   ,   =(0,2,0),因此   ·   =0. 从而   ⊥   ,所以 EF ⊥ BC . (2)解法一:在图1中,过 O 作 OG ⊥ BF ,垂足为 G ,连 EG .由平面 ABC ⊥平面 BDC ,从而 EO ⊥面 BDC , 又 OG ⊥ BF ,由三垂线定理知 EG ⊥ BF . 因此∠ EGO 为二面角 E - BF - C 的平面角. 在△ EOC 中, EO =   EC =   BC ·cos 30 ° =   , 由△ BGO ∽△ BFC 知, OG =   · FC =   , 因此tan∠ EGO =   =2, 从而sin∠ EGO =   , 即二面角 E - BF - C 的正弦值为   . 解法二:在图2中,平面 BFC 的一个法向量为 n 1 =(0,0,1). 设平面 BEF 的法向量为 n 2 =( x , y , z ), 又   =   ,   =   , 由   得其中一个 n 2 =(1,-   ,1). 评析 　本题考查空间位置关系的证明及空间角的求法.本题的难点和易错点都是空间直角坐 标系的建立,由于 A 、 D 两点都不在坐标轴上,因此正确求出 A 、 D 两点的坐标是解决本题的关 键. cos θ =|cos< n 1 , n 2 >|=       =   , 因此sin θ =   =   ,即所求二面角的正弦值为   . 设二面角 E - BF - C 的大小为 θ ,且由题意知 θ 为锐角,则 考点　直线、平面垂直的判定与性质 1. (2015湖南,19,13分)如图,已知四棱台 ABCD - A 1 B 1 C 1 D 1 的上、下底面分别是边长为3和6的正方 形, A 1 A =6,且 A 1 A ⊥底面 ABCD .点 P , Q 分别在棱 DD 1 , BC 上. (1)若 P 是 DD 1 的中点,证明: AB 1 ⊥ PQ ; (2)若 PQ ∥平面 ABB 1 A 1 ,二面角 P - QD - A 的余弦值为   ,求四面体 ADPQ 的体积.   C组  教师专用题组 解析 　解法一:由题设知, AA 1 , AB , AD 两两垂直.以 A 为坐标原点, AB , AD , AA 1 所在直线分别为 x 轴, y 轴, z 轴,建立如图所示的空间直角坐标系,则相关各点的坐标为 A (0,0,0), B 1 (3,0,6), D (0,6,0), D 1 (0, 3,6), Q (6, m ,0),其中 m = BQ ,0 ≤ m ≤ 6.   (1)若 P 是 DD 1 的中点,则 P   ,   =   .又   =(3,0,6), 于是   ·   =18-18=0,所以   ⊥   ,即 AB 1 ⊥ PQ . (2)由题设知,   =(6, m -6,0),   =(0,-3,6)是平面 PQD 内的两个不共线向量.设 n 1 =( x , y , z )是平面 PQD 的法向量,则   即   取y=6,得 n 1 =(6- m ,6,3).又平面 AQD 的一个法向 量是 n 2 =(0,0,1), 所以cos< n 1 , n 2 >=   =   =   . 而二面角 P - QD - A 的余弦值为   ,因此   =   ,解得 m =4,或 m =8(舍去),此时 Q (6,4,0). 设   = λ   (0< λ ≤ 1),而   =(0,-3,6),由此得点 P (0,6-3 λ ,6 λ ),所以   =(6,3 λ -2,-6 λ ). 因为 PQ ∥平面 ABB 1 A 1 ,且平面 ABB 1 A 1 的一个法向量是 n 3 =(0,1,0),所以   · n 3 =0,即3 λ -2=0,亦即 λ =   ,从而 P (0,4,4). 于是,将四面体 ADPQ 视为以△ ADQ 为底面的三棱锥 P - ADQ ,则其高 h =4.故四面体 ADPQ 的体积 V =   S △ ADQ · h =   ×   × 6 × 6 × 4=24. 解法二:(1)如图a,取 A 1 A 的中点 R ,连接 PR , BR .因为 A 1 A , D 1 D 是梯形 A 1 ADD 1 的两腰, P 是 D 1 D 的中 点,所以 PR ∥ AD ,于是由 AD ∥ BC 知, PR ∥ BC ,所以 P , R , B , C 四点共面. 由题设知, BC ⊥ AB , BC ⊥ A 1 A ,所以 BC ⊥平面 ABB 1 A 1 ,因此 BC ⊥ AB 1 .① 因为tan∠ ABR =   =   =   =tan∠ A 1 AB 1 ,所以∠ ABR =∠ A 1 AB 1 ,因此∠ ABR +∠ BAB 1 =∠ A 1 AB 1 + ∠ BAB 1 =90 ° , 于是 AB 1 ⊥ BR .再由①即知 AB 1 ⊥平面 PRBC . 又 PQ ⊂ 平面 PRBC ,故 AB 1 ⊥ PQ .   图a 图b        (2)如图b,过点 P 作 PM ∥ A 1 A 交 AD 于点 M ,则 PM ∥平面 ABB 1 A 1 .② 因为 A 1 A ⊥平面 ABCD ,所以 PM ⊥平面 ABCD .过点 M 作 MN ⊥ QD 于点 N ,连接 PN ,则 PN ⊥ QD ,∠ PNM 为二面角 P - QD - A 的平面角,所以cos∠ PNM =   ,即   =   ,从而   =   .③ 连接 MQ ,由 PQ ∥平面 ABB 1 A 1 及②知,平面 PQM ∥平面 ABB 1 A 1 ,所以 MQ ∥ AB .又 ABCD 是正方形, 所以 ABQM 为矩形,故 MQ = AB =6. 设 MD = t ,则 MN =   =   .④ 过点 D 1 作 D 1 E ∥ A 1 A 交 AD 于点 E ,则 AA 1 D 1 E 为矩形,所以 D 1 E = A 1 A =6, AE = A 1 D 1 =3,因此 ED = AD - AE =3.于是   =   =   =2,所以 PM =2 MD =2 t . 再由③,④得   =   ,解得 t =2,因此 PM =4.故四面体 ADPQ 的体积 V =   S △ ADQ · PM =   ×   × 6 × 6 × 4=24. 2. (2014广东,18,13分)如图,四边形 ABCD 为正方形, PD ⊥平面 ABCD ,∠ DPC =30 ° , AF ⊥ PC 于 点 F , FE ∥ CD ,交 PD 于点 E . (1)证明: CF ⊥平面 ADF ; (2)求二面角 D - AF - E 的余弦值.   解析 　(1)证明:∵ PD ⊥平面 ABCD ,∴ PD ⊥ AD , 又 CD ⊥ AD , PD ∩ CD = D , ∴ AD ⊥平面 PCD ,∴ AD ⊥ PC , 又 AF ⊥ PC , AF ∩ AD = A , ∴ PC ⊥平面 ADF ,即 CF ⊥平面 ADF . (2)解法一:设 AB =1,则Rt△ PDC 中, CD =1,∵∠ DPC =30 ° , ∴ PC =2, PD =   ,由(1)知 CF ⊥ DF , ∴ DF =   ,∴ CF =   ,又 FE ∥ CD , ∴   =   =   ,∴ DE =   ,同理, EF =   CD =   , 如图所示,以 D 为原点,建立空间直角坐标系,则 A (0,0,1),   E   , F   , P (   ,0,0), C (0,1,0). 设 m =( x , y , z )是平面 AEF 的法向量, 则   又   ∴   令 x =4,得 z =   ,故 m =(4,0,   ), 由(1)知平面 ADF 的一个法向量为   =(-   ,1,0),设二面角 D - AF - E 的平面角为 θ ,可知 θ 为锐角, cos θ =|cos< m ,   >|=   =   =   ,故二面角D-AF-E的余弦值为   . 解法二:设 AB =1, ∵ CF ⊥平面 ADF ,∴ CF ⊥ DF . ∴在△ CFD 中, DF =   , ∵ CD ⊥ AD , CD ⊥ PD , ∴ CD ⊥平面 ADE .又∵ EF ∥ CD , ∴ EF ⊥平面 ADE .∴ EF ⊥ AE , ∴在△ DEF 中, DE =   , EF =   , 在△ ADE 中, AE =   ,在△ ADF 中, AF =   . 由 V A - DEF =   · S △ ADE · EF =   · S △ ADF · h E - ADF , 解得 h E - ADF =   , 设△ AEF 的边 AF 上的高为 h , 由 S △ AEF =   · EF · AE =   · AF · h ,解得 h =   ×   , 设二面角 D - AF - E 的平面角为 θ ,可知 θ 为锐角. 则sin θ =   =   ×   ×   =   , ∴cos θ =   . 3. (2014江西,19,12分)如图,四棱锥 P - ABCD 中, ABCD 为矩形,平面 PAD ⊥平面 ABCD . (1)求证: AB ⊥ PD ; (2)若∠ BPC =90 ° , PB =   , PC =2,问 AB 为何值时,四棱锥 P - ABCD 的体积最大?并求此时平面 BPC 与平面 DPC 夹角的余弦值.   解析 　(1)证明: ABCD 为矩形,故 AB ⊥ AD . 又平面 PAD ⊥平面 ABCD ,平面 PAD ∩ 平面 ABCD = AD , 所以 AB ⊥平面 PAD ,故 AB ⊥ PD . (2)过 P 作 AD 的垂线,垂足为 O ,过 O 作 BC 的垂线,垂足为 G ,连接 PG .   故 PO ⊥平面 ABCD , BC ⊥平面 POG , BC ⊥ PG . 在Rt△ BPC 中, PG =   , GC =   , BG =   . 设 AB = m ,则 OP =   =   ,故四棱锥 P - ABCD 的体积 V =   ·   · m ·   =     . 因为 m   =   =   , 故当 m =   ,即 AB =   时,四棱锥 P - ABCD 的体积最大. 此时,建立如图所示的坐标系,各点的坐标为 O (0,0,0), B   , C   , D   , P   . 故   =   ,   =(0,   ,0),   =   . 设平面 BPC 的一个法向量为 n 1 =( x , y ,1),则由 n 1 ⊥   , n 1 ⊥   得   解得 x =1, y = 0, n 1 =(1,0,1).同理可求出平面 DPC 的一个法向量为 n 2 =   . 从而平面 BPC 与平面 DPC 夹角 θ 的余弦值为cos θ =   =   =   . 评析     本题考查面面垂直的性质定理、线线垂直的判定、空间几何体的体积以及二面角的 求解等基础知识,考查空间想象能力、推理论证能力和运算求解能力,正确利用面面垂直的性 质定理求出棱锥的高是解决本题的关键.计算错误是失分的主要原因. 4. (2013课标Ⅰ,18,12分,0.524)如图,三棱柱 ABC - A 1 B 1 C 1 中, CA = CB , AB = AA 1 ,∠ BAA 1 =60 ° . (1)证明: AB ⊥ A 1 C ; (2)若平面 ABC ⊥平面 AA 1 B 1 B , AB = CB ,求直线 A 1 C 与平面 BB 1 C 1 C 所成角的正弦值.   解析 　(1)证明:取 AB 的中点 O ,连接 OC , OA 1 , A 1 B . 因为 CA = CB ,所以 OC ⊥ AB . 由于 AB = AA 1 ,∠ BAA 1 =60 ° ,故△ AA 1 B 为等边三角形,所以 OA 1 ⊥ AB . 因为 OC ∩ OA 1 = O ,所以 AB ⊥平面 OA 1 C . 又 A 1 C ⊂ 平面 OA 1 C ,故 AB ⊥ A 1 C . (2)由(1)知 OC ⊥ AB , OA 1 ⊥ AB . 又平面 ABC ⊥平面 AA 1 B 1 B ,交线为 AB ,所以 OC ⊥平面 AA 1 B 1 B ,故 OA , OA 1 , OC 两两相互垂直. 以 O 为坐标原点,   的方向为 x 轴的正方向,|   |为单位长,建立如图所示的空间直角坐标系 O - xyz .   由题设知 A (1,0,0), A 1 (0,   ,0), C (0,0,   ), B (-1,0,0). 则   =(1,0,   ),   =   =(-1,   ,0),   =(0,-   ,   ). 设 n =( x , y , z )是平面 BB 1 C 1 C 的法向量, 则   即   可取 n =(   ,1,-1). 故cos< n ,   >=   =-   . 所以 A 1 C 与平面 BB 1 C 1 C 所成角的正弦值为   . 思路分析 　(1)取 AB 的中点 O ,由已知条件可得 OC ⊥ AB , OA 1 ⊥ AB ,从而得 AB ⊥平面 OA 1 C ,从而 得 AB ⊥ A 1 C ;(2)根据证得的垂直关系建立空间直角坐标系,求出平面 BB 1 C 1 C 的一个法向量,进而 求出该法向量与   夹角的余弦值,从而可得直线 A 1 C 与平面 BB 1 C 1 C 所成角的正弦值. 规律总结 　面面垂直的性质定理在立体几何中是一个极为关键的定理,这个定理的主要作用 是将面面垂直问题转化为线面垂直问题.在一些垂直关系的证明及线面角、二面角的求解中, 常要借助这个定理作出平面的垂线. 5. (2012课标,19,12分)如图,直三棱柱 ABC - A 1 B 1 C 1 中, AC = BC =   AA 1 , D 是棱 AA 1 的中点, DC 1 ⊥ BD . (1)证明: DC 1 ⊥ BC ; (2)求二面角 A 1 - BD - C 1 的大小.   解析 　(1)由题设知,三棱柱的侧面为矩形. 由于 D 为 AA 1 的中点,故 DC = DC 1 .又 AC =   AA 1 ,可得 D   + DC 2 = C   ,所以 DC 1 ⊥ DC .而 DC 1 ⊥ BD , DC ∩ BD = D ,所以 DC 1 ⊥平面 BCD .又 BC ⊂ 平面 BCD ,故 DC 1 ⊥ BC . (2)由(1)知 BC ⊥ DC 1 ,且 BC ⊥ CC 1 ,则 BC ⊥平面 ACC 1 , 所以 CA , CB , CC 1 两两相互垂直. 以 C 为坐标原点,   的方向为 x 轴的正方向,   的方向为 y 轴的正方向,|   |为单位长,建立如图 所示的空间直角坐标系 C - xyz .   由题意知 A 1 (1,0,2), B (0,1,0), D (1,0,1), C 1 (0,0,2). 则   =(0,0,-1),   =(1,-1,1),   =(-1,0,1). 设 n =( x , y , z )是平面 A 1 B 1 BD 的法向量, 则   即   可取 n =(1,1,0). 同理,设 m 是平面 C 1 BD 的法向量,则   可取 m =(1,2,1).从而cos< n , m >=   =   . 又易知二面角 A 1 - BD - C 1 为锐二面角, 故二面角 A 1 - BD - C 1 的大小为30 ° . 评析     本题考查了直线与直线垂直的证明及二面角的求法.属中等难度题,运算要准确. 考点　直线、平面垂直的判定与性质 1. (2018湖北重点中学协作体4月联考,5)设 m , n 是平面 α 内的两条不同直线, l 1 , l 2 是平面 β 内两条相 交直线,则 α ⊥ β 的一个充分不必要条件是   (　　) A. l 1 ⊥ m , l 1 ⊥ n 　    B. m ⊥ l 1 , m ⊥ l 2 C. m ⊥ l 1 , n ⊥ l 2 　    D. m ∥ n , l 1 ⊥ n A 组  2016—2018年高考模拟·基础题组 三年模拟 答案    B 　由 m ⊥ l 1 , m ⊥ l 2 及已知条件可得 m ⊥ β ,又 m ⊂ α ,所以 α ⊥ β ;反之, α ⊥ β 时未必有 m ⊥ l 1 , m ⊥ l 2 ,故“ m ⊥ l 1 , m ⊥ l 2 ”是“ α ⊥ β ”的充分不必要条件,其余选项均推不出 α ⊥ β ,故选B. 2. (2017中原名校联盟4月联考,4)已知 m 和 n 是两条不同的直线, α 和 β 是两个不重合的平面,下面 给出的条件中一定能推出 m ⊥ β 的是   (　　) A. α ⊥ β 且 m ⊂ α 　    B. α ⊥ β 且 m ∥ α C. m ∥ n 且 n ⊥ β 　    D. m ⊥ n 且 n ∥ β 答案    C 　对于选项A, α ⊥ β 且 m ⊂ α ,可得 m ∥ β 或 m 与 β 相交或 m ⊂ β ,故A不成立;对于选项B, α ⊥ β 且 m ∥ α ,可得 m ⊂ β 或 m ∥ β 或 m 与 β 相交,故B不成立;对于选项C, m ∥ n 且 n ⊥ β ,则 m ⊥ β ,故C正确; 对于选项D,由 m ⊥ n 且 n ∥ β ,可得 m ∥ β 或 m 与 β 相交或 m ⊂ β ,故D不成立.故选C. 3 .(2017河南百校联盟联考,11)如图,已知等腰直角三角形 ABC , AB = AC ,将△ ABC 沿斜边 BC 向上翻转,与原图形构成几何体 A 1 - ABC ,其外接球表面积为4π,设二面角 A 1 - BC - A 的平面角为 α ,若 O 为 BC 的中点,点 P , Q 分别为线段 OA 1 , AB 的中点,则当 PQ =   时,角 α 等于   (　　) A.   　    B.   　    C.   　    D.   答案    B 　连接 OQ ,根据题意知几何体 A 1 - ABC 的外接球的球心为 O ,半径为 OB = OC = OA = OA 1 , 则4π· OB 2 =4π,∴ OB =1,所以 BC =2,故 OQ =   , OP =   ,从而当 PQ =   时, PQ 2 = OP 2 + OQ 2 ,∴ OP ⊥ OQ .又 OP ⊥ BC , OQ ∩ BC = O ,所以 OP ⊥平面 ABC ,所以平面 A 1 BC ⊥平面 ABC ,即 α =   . 4. (2018河南商丘二模,15)如图, PA ⊥圆 O 所在的平面, AB 是圆 O 的直径, C 是圆 O 上的一点, E 、 F 分别是 A 在 PB 、 PC 上的射影,给出下列结论: ① AF ⊥ PB ;② EF ⊥ PB ;③ AF ⊥ BC ;④ AE ⊥平面 PBC . 其中正确命题的序号是 　　　     .   答案 　①②③ 解析 　由 PA ⊥平面 ABC , BC ⊂ 平面 ABC ,可得 PA ⊥ BC ,又 AB 是圆 O 的直径, C 是圆 O 上一点,则有 BC ⊥ AC ,又 PA ∩ AC = A ,所以 BC ⊥面 PAC ,又 AF ⊂ 面 PAC ,所以 BC ⊥ AF ,故③正确;因为 AF ⊥ PC , PC ∩ BC = C ,所以 AF ⊥面 PBC ,又 PB ⊂ 面 PBC ,所以 AF ⊥ PB ,故①正确;因为 AE ⊥ PB , AF ⊥ PB , AE ∩ AF = A ,所以 PB ⊥平面 AEF ,又 EF ⊂ 平面 AEF ,所以 PB ⊥ EF ,故②正确;由于 AF ⊥平面 PBC , AF ∩ AE = A ,所以 AE 不与面 PBC 垂直,故④错误.综上可知正确命题的序号为①②③. 5.(2018河南郑州二模,19) 如图所示,在四棱锥 P - ABCD 中, PA ⊥平面 ABCD ,△ DAB ≌△ DCB , E 为线段 BD 上的一点,且 EB = ED = EC = BC ,连接 CE 并延长交 AD 于 F . (1)若 G 为 PD 的中点,求证:平面 PAD ⊥平面 CGF ; (2)若 BC =2, PA =3,求平面 BCP 与平面 DCP 所成锐二面角的余弦值. 解析 　(1)证明:在△ BCD 中, EB = ED = EC = BC ,故∠ BCD =   ,∠ CBE =∠ CEB =   , 连接 AE ,∵△ DAB ≌△ DCB ,∴△ EAB ≌△ ECB , 从而有∠ FED =∠ BEC =∠ AEB =   , AE = CE = DE .   (3分) ∴∠ AEF =∠ FED =   ,故 EF ⊥ AD , AF = FD . 又 PG = GD ,∴ FG ∥ PA . 又 PA ⊥平面 ABCD ,故 GF ⊥平面 ABCD , ∴ GF ⊥ AD ,又 GF ∩ EF = F ,故 AD ⊥平面 CFG . 又 AD ⊂ 平面 PAD ,∴平面 PAD ⊥平面 CGF .   (6分) 则   解得   即 n 1 =   .   (9分) 设平面 DCP 的一个法向量为 n 2 =(1, y 2 , z 2 ), 则   解得   即 n 2 =(1,   ,2). 从而平面 BCP 与平面 DCP 所成锐二面角的余弦值为   =   =   .   (12分) (2)以点 A 为坐标原点建立如图所示的空间直角坐标系, 则 A (0,0,0), B (2,0,0), C (3,   ,0), D (0,2   ,0), P (0,0,3). 故   =(1,   ,0),   =(-3,-   ,3),   =(-3,   ,0). 设平面 BCP 的一个法向量为 n 1 =(1, y 1 , z 1 ), 6. (2018安徽江淮十校4月联考,18)四棱锥 A - BCDE 中, EB ∥ DC ,且 EB ⊥平面 ABC , EB =1, DC = BC = AB = AC =2, F 是棱 AD 的中点. (1)证明: EF ⊥平面 ACD ; (2)求二面角 B - AE - D 的余弦值.   解析 　(1)证明:取 AC 中点 M ,连接 FM 、 BM ,   ∵ F 是 AD 中点,∴ FM ∥ DC ,且 FM =   DC =1. 又∵ EB ∥ DC , EB =1,∴ FM